基于滤波法的稳态检测

2011-04-11王晓锋

科学之友 2011年16期

王晓锋，曾超

（宁波万华聚氨酯有限公司，浙江宁波 315812）

1 基于滤波法的稳态检测原理

滤波法是一种常用的稳态检测方法。在滤波法中，如下统计量用于稳态检测。

式中，si为变量i的均值检验量，ci为变量i的方差检测量，si～N（0，1），ci～x2（n），n 为测量次数，eij为变量 i第 j次测量值滤波前后的偏差量，əi为变量i的测量方差。当|si|＞s（α）或者|ci|＞c（α）时（α为置信度），过程处于非稳态，反之过程处于稳态。

上述滤波法假设测量数据只含随机误差，但这个假设有不合理的成分，因为实际生产过程中测量变量常含有过失误差。稳态检测是稳态过失误差侦破与识别、数据校正和协调的前提条件，如果认为测量变量不含有过失误差，则没有必要进行过失误差侦破与识别。在不确定测量变量是否含有过失误差的情况下，应用滤波法进行稳态检测理论依据不足；在确定测量变量含有过失误差的情况下，由于不满足上述滤波法的假设，用滤波法进行稳态检测的结果不可靠。因此，将这条假设修改成：测量数据含随机误差和过失误差，随机误差服从零均值正态分布；过失误差服从均值为，方差为 ∂'2的任意分布，和 ∂'2为常数， ∂'2可由过程数据估计。

基于新的假设从新建立用于稳态检测的统计量，测量模型表示为：

其中：xij为变量i的第j次测量值，为变量i的第j次测量值的真值，ξij为变量i的第j次测量值的随机误差，θij为变量i的第j次测量值的过失误差为变量i的测量过失误差均值，为变量i的测量过失误差方差。

式中，xi为变量i的测量值，为xi的滤波值，Tf为滤波时间常数（MIN），令a =，T为采样周期（MIN），将上式s变换后有：0）＝x（i0）（5）

根据中心极限定理，n→∞时（实际过程中n比较大，近似满足）。

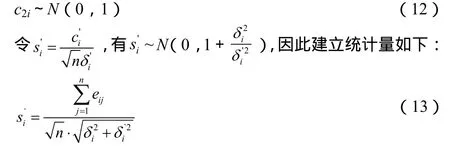
方差检验统计量推导如下：

在新假设的基础上，需要增加一个附加条件，即认为 θij~N），此时有：eij～N（0，）（14）

由没修改前的滤波法基本假设中的不足，指出该方法不能应用于含过失误差数据的稳态检测。基于新的假设，推导出适用于含过失误差数据稳态检测的统计量。当数据不含过失误差时，从新统计量又能推导出原方法统计量。说明新方法适用条件更广。数值实验结果表明，当测量数据含有过失误差时，原滤波法不能有效地进行稳态检测，甚至完全失败，而改进后的方法可以得到满意的结果。