卡诺图在继电 接触器控制电路触点化简中的应用研究
2011-04-10运城学院机电工程系山西运城044000
(运城学院机电工程系,山西 运城044000)
在设计继电-接触器控制电路时,经常遇到同一标号触点多次出现的现象,为了简化电路并节约成本,设计时必须对触点进行化简。在继电-接触器控制电路触点化简时,具体方法有逻辑表达式化简和经验法化简,前者需要设计者具有良好的数学推导能力,当控制电路较复杂时,由于逻辑表达式过于繁琐,数学推导过程极易出错,并不实用;后者则主要取决于设计者的电气控制设计经验,其化简结果往往不是最简电路。因此,寻找一种理论较简单、应用不复杂的化简工具对于继电-接触器控制电路设计具有重要意义。笔者将常用于电子电路化简的卡诺图应用于继电-接触器控制电路触点化简,研究了卡诺图在继电-接触器控制电路触点化简中的应用情况。
1 卡诺图的基本原理
卡诺图是1953年由美国工程师 Maorice Karnaugh提出的一种逻辑函数化简的系统方法[1],它将有n个变量的逻辑函数的2n个最小项组织排列在给定的方格矩阵中,为相邻最小项(相邻与项)运用邻接律化简,提供了直观的几何图形表示工具[2]。与代数法相比,卡诺图法主要有以下特点:①卡诺图中的每个小方格对应一个最小项。②卡诺图具有循环相邻的特性,即图中同一行里最左和最右端的小方格是相邻的,同一列里最上和最下端的小方格也是相邻的。③逻辑相邻的最小项在几何位置上也相邻[3]。

图1 逻辑函数的卡诺图
逻辑函数卡诺图如图1所示,图1(a)图为1个4变量的卡诺图,每个小方格所代表的最小项用对应的阿拉伯数值标明,可以表示为F(A,B,C,D)= ∑m。自变量的取值一般按格雷码排列[4],可保证卡诺图的相邻性。图1(b)图所示为某4变量逻辑函数F(A,B,C,D)= ∑m(2,3,5,6,7,10,11,14,15)的卡诺图,在填写卡诺图时,F所包含的最小项对应的小方格写入1,F不含的最小项对应的小方格写入0[4]。
卡诺图化简时,需找出图中几何位置相邻的 “1”格,用圆圈圈起来,其圆圈称为卡诺圈,将一个卡诺圈合并为一个最小项,消去取值有变化的变量[5],这样合并后表达式中变量的个数会逐渐减少,最终达到化简的目的。
图1(b)可以采用图2所示的卡诺圈进行化简,图中包含一大一小两个卡诺圈,大圈包含了变量A、B、D的所有取值,故化简结果为变量C;小圈中变量A、B、D取值为A=0、B=1、D=1,变量C两种取值均被包含,故化简后消去变量C,结果为ABD。化简结果相加后得到整体化简结果F,如下式:


图2 图1(b)的卡诺图化简
2 卡诺图的应用
2.1 电路的逻辑函数转换
由于继电-接触器电路一般采用图形表现形式,而卡诺图只针对逻辑函数,所以在使用卡诺图化简触点电路时,首先要将继电-接触器电路用逻辑函数最小项的形式表示出来。一个继电-接触器电路往往包含多条支路,大多数支路可能并不需要化简,所以一般只对包含多个相同标号的触点支路进行逻辑函数转换。通常将控制电路中每一个需化简的执行器件,如接触器、继电器、电磁阀的线圈以及主电路中电动机的绕组,作为逻辑函数的结果F,将各个触点作为逻辑函数的因子k,其常开触点用k表示,常闭触点用k表示。转换时串联的各触点以“积”的形式表示,并联的各触点以“和”的形式表示。电路中的按钮以及自、互锁单元往往受到装配和控制操作的限制,如果改变会影响系统的操作性、可靠性,故不参与化简,可以排除在逻辑表达式以外。为了提高电路的安全性,一般也不对电路的保护器件(如融断器、热继电器等)进行化简,保护电器也排除在逻辑表达式以外。值得注意的是,继电-接触器电路的主、辅触点在电路中不能够相互替代,因此必须避免将主电路和控制电路表现在同一个逻辑函数中。
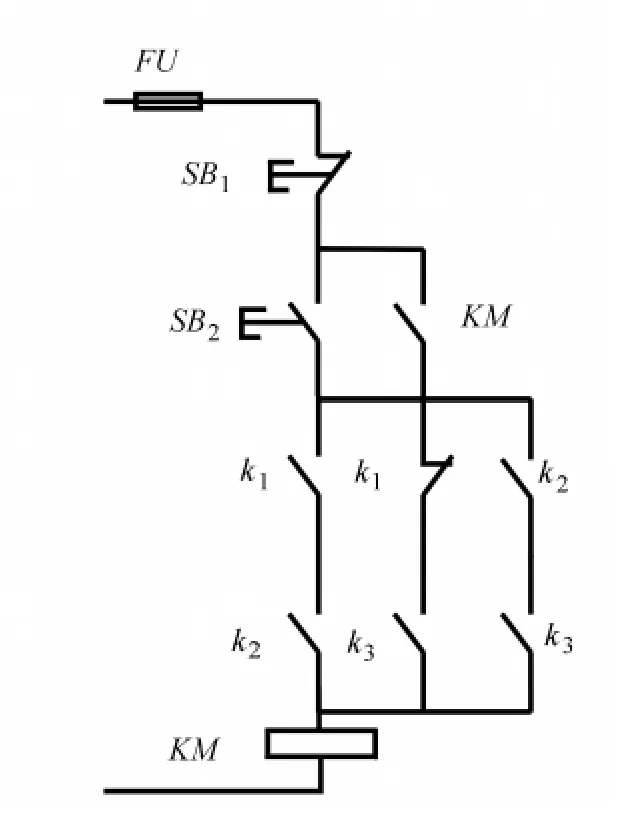
图3 控制电路图
遵照以上转换要求,图3所示的电路在不考虑融断器、按钮及自锁环节后,可以写成下列逻辑函数表达形式:

式中,F代表接触器KM线圈的状态;k1、k2、k3分别代表图3中继电器的常开触点;为k1的常闭触点。
2.2 画卡诺图并化简
将电路变化成逻辑函数的形式后,按卡诺图的绘制要求找到这些最小项对应的位置,填入1,其余位置填入0,然后用卡诺圈将相邻的填写1的小方格合并为一个乘积项,合并取值变化的变量,逐次进行化简后可得到最简式。
将式(2)画出其对应卡诺图,并确定合并项,画出卡诺圈,如图4所示。

图4 式(1)对应的卡诺图
图4中2个卡诺圈分别包含了触点k3和k2的2种取值,分别可以化简为,合成后原控制线路可写成最小项表达式:

2.3 将化简后的最简式再回画成电路形式
化简后的最小项表达式需重新画成电路的表现形式,最小项积以触点串联形式表示,最小项和以触点并联形式表示,最小项表达式结果F转化为电路的执行器件,这样即得到触点化简后的电路。式(3)重新变成电路图的形式如图5所示。
将每一组逻辑表达式均化简,并变成电路形式后,将各个子电路合并成一个电路。再将所省略的电路按钮、自互锁单元、保护器件恢复到电路中原来的位置。由于各个最简控制单元间有可能存在相互关系,在合并电路后需对各个电路执行器件进行统一检查,确保化简前后控制逻辑关系不发生变化。需要说明的是,同一电路不同执行器件在采用卡诺图化简时相互独立,其化简后的最简逻辑表达式间有可能存在共同项,即化简后不同执行器件的电路中存在相同的触点组合,其逻辑表达式仍然可以用卡诺图进行关联化简,卡诺图本身确实具有同时化简多个相关逻辑函数的能力[2-4],但是由于继电-接触器电路本身的特点,一般不再对不同执行器件电路中的相同触点进行化简,否则有可能改变控制逻辑和操作关系,从而导致控制混乱。这是卡诺图在继电-接触器电路和电子逻辑电路触点化简中最大的不同。例如某控制电路的2个支路写成逻辑表达式为:如果进行卡诺图关联化简,则可得到含有相同项的卡诺图形式(见图6),其最简式均包含最小项卡诺图本身允许将最小项合并为F1、F2共用形式[6]。将图6改画后的电路形式如图7所示。正确的化简电路如图7(a)所示,由于关化简后改变了控制的逻辑关系(见图7(b)),因而该化简是不正确的。

图5 化简后的控制电路

图6 2个具有相同项的卡诺图
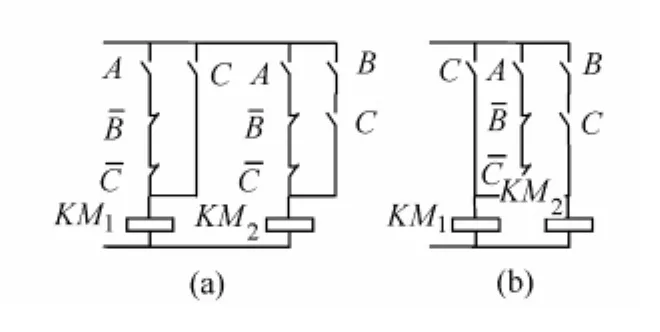
图7 图6改画后的电路形式
3 结 语
将卡诺图应用于继电-接触器控制电路触点化简,可以将复杂的继电-接触器触点电路变成结构简单、控制过程清晰的简化电路,从而降低控制电路设计成本,提高系统的可靠性,是一种继电-接触器控制电路触点化简的好方法。
[1]Karnaugh M.The map method for synthesisf combinational logic circuits [J].Transactions of American institute of elect rical engineers,1953,72:593-599.
[2]王平均,吴恒玉,黄果.卡诺图在教学中的应用 [J].装备制造技术,2009(3):177-179.
[3]陈小芳.逻辑函数的卡诺图化简法 [J].计算机时代,2010(8):49-51.
[4]卢容德.联合卡诺图在逻辑电路分析中的应用 [J].长江大学学报(自然科学版),2009,6(4):N61-65.
[5]李晓明.电路与电子技术 [M].北京:高等教育出版社,2004.
[6]韩天荣.具有多输出端逻辑电路化简的卡诺图法 [J].集宁师专学报,2005,27(12):16-17.
