基于船舶大修的人力资源优化配置研究＊

侯莉莉 姚玉南 范世东 江 攀

（武汉理工大学能源与动力工程学院 武汉 430063）

船舶大修是根据船舶的状况、规范的要求由船东有计划的安排船舶进入专业修船厂进行全面的检查、修理以及船舶证书的办理.维修人力资源是船舶大修的重要资源，目前大多数修船厂对维修人力资源的分配是根据以往的修船经验来进行的，没有形成一种科学的维修人力资源管理方法［1－2］.文中通过建立维修人员实时技能矩阵来显示维修人员的工作能力，并在船舶大修计划已定的条件下，以维修人员数量和能力差异为约束，完成维修任务为目标建立维修人力资源的优化模型.应用遗传算法对此优化模型进行求解，得出最优的配置模型.维修人员的合理分配将会缩短维修时间，降低维修费用及船舶停运的损失.

1 船舶大修工作次序模型与人力资源技能关系模型

1.1 工作次序模型

依据船舶大修所编制的修理单建立维修次序工作流模型，首先要将维修项目进行分解，理清维修项目之间的关联次序，再按照关联次序建立工作流模型.对于复杂的船舶维修项目，可以先分为若干子系统，子系统可再细分为次级子系统.根据船舶大修任务的实际需要，一般可细分到具有一定功能的设备，通常把具有一定功能设备的维修称为一个维修工作项目.

维修项目之间的关联次序是串联与并联的组合.串联的维修项目受到维修次序的约束，并联的维修项目则不受维修次序的约束可以同时开工.根据确定的维修项目制定维修计划，建立维修工作流程图，再配以合理的维修人力，使维修总耗时达到最短.如图1所示某设备的维修工作流模型.

图1 维修工作流模型图

1.2 维修人员技能矩阵

由于各项维修任务对维修人员技能要求不同，且每个维修人员所擅长的维修项目也有一定差异.所以对维修人力资源进行优化配置，首先要了解修船厂维修人员做不同维修工作时的维修技能.本文通过建立维修人员的技能矩阵（skill matrix，SM）来反映不同维修人员在做不同维修工作时的效果.该技能矩阵时根据维修人员完成不同维修任务时所用的时间和任务完成的情况来评估和制定.考虑到维修人员有限的约束，假设有n（M1，M2，…，Mn）项维修任务，m（P1，P2，…，Pm）名维修人员（m＜n），每一名维修人员均可分配给各项维修项目，但是每一位人员的维修能力是有差异的，以aij表示维修人员i完成维修项目j的工作能力.文中把维修能力分为六个等级，每个等级对应的aij值分别为0，0.5，1.0，1.5，2.0，2.5，规定第三等级是标准的维修能力（即aij＝1）.aij数值越大，工作能力越强，aij＝0表示人员Pi不能胜任Mj项目的维修工作.则技能矩阵可用如下表示.

2 船舶大修人力资源优化配置模型

2.1 人力资源优化配置模型

在总维修任务进度范围内，应给每一位维修人员分配与其相适应的维修项目.以达到设备总维修完成时间最短的目的.设某设备有n个维修项目，维修总工时为T，根据维修项目间的关联次序把维修总工时分为t个阶段.有m（m＜n）名维修人员，维修人员i完成维修项目j的工作能力值为aij.每项维修项目的定额维修工作量为常数Epj.据此给出组合优化模型.

式中：Tt为按维修项目的预定维修次序，将维修总耗时T分成若干时段，端点为各项目的起点或终点，总段数为t段；所有的维修项目都有确定的定额维修工作量，即常数Epj，表示一个具有标准工作能力的维修人员所需花费的维修时间（以标准工作能力与维修时间的乘积求得）.维修项目在各个时段的累积维修工作量必须大于定额维修工作量，才能完成该维修项目；D（t）ij为维修人员i在时段Tt是否正在从事项目j的维修，D（t）ij＝1时表示正在从事，D（t）ij＝0时表示没有从事.且在各个时间段Tt内，每一个维修人员最多只从事一个维修工作项目；f（j，t）为j项目在Tt时间段内是否正在被维修，取值为0或者1.

2.2 优化数学模型求解

上述模型表达了一般性的优化模型表达方式.现以图1中具体的设备维修次序为例进行优化.图1中某设备共有7项维修任务，其中维修任务M1，M2，M3，M4为串联关系，即存在维修次序上的约束.根据串联的维修次序约束把维修总工时T 分为T1，T2，T3，T44个时间段.维修任务M5在M1完工之后即可开工，并在时间段T2，T3内完工；M6在 M1，M2之后开工，并在T3，T4时间段内完工.M7在 M1之后开工，在T2，T3，T4时间段内完工.

对图1中某设备的维修人力资源优化模型展开为下面的具体优化.

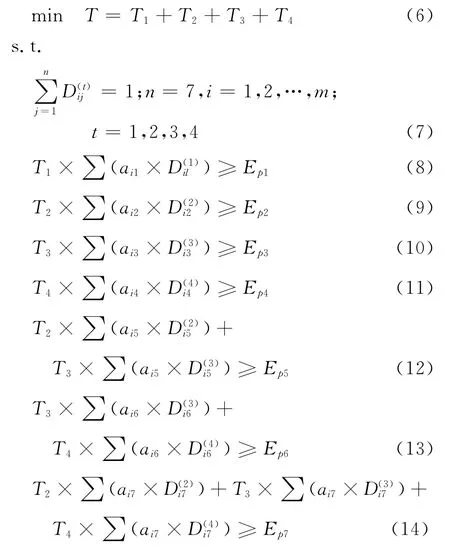
此数学模型为NP线性规划问题，用遗传算法可以快速求解此类问题.遗传算法（genetic algorithm）是一类借鉴生物界的自然选择和遗传进化机制而开发的一种全局优化自适应概率搜索方法［3－4］.本文应用英国设菲尔德大学开发的遗传算法工具箱来解决问题［5］.

遗传算法的主要步骤有编码、选择、交叉、变异、适应度函数的设计、约束条件与终止准则.

1）编码 在遗传算法中，把一个问题的可行解从解空间转换到遗传算法所能处理的搜索空间，这种转换方式称为编码.在本文中采用二进制编码.

本文中依据图1所示的维修工作流程图的具体编码如下：把总染色体串分为四个阶段.第一阶段基因值有一种，维修项目1，编码的前六位0，1都表示项目1正在维修；第二阶段基因值有三种，维修项目2，5和7，分别用01，10，11表示；第三阶段基因值有四种维修项目3，5，6和7，分别用00，01，10，11来表示；第四阶段基因值有维修项目4，6和7三种，用01，10，11表示.如随机产生的染色体［000110 011001101110 001010000101 111001111110］.

2）适应度函数 遗传算法中以个体适应度的大小来确定该个体被遗传到下一代群体中的概率.英国设菲尔德大学开发的遗传算法工具箱中的ranking函数，格式：FitnV＝ranking（ObjV），是按照个体的目标值ObjV由小到大的顺序对它们进行排序.本文中应用ranking函数来分配适应度值.

3）选择 选择又称复制，是在种群中选择适应能力强的个体产生新的种群的过程，rws函数是在当前种群中按照它们的适应度FitnV选择Nsel个个体繁殖.

4）交叉 交叉运算是遗传算法中产生新个体的主要操作过程，它以某一概率相互交换某两个个体之间的部分染色体.本文取Pc＝0.7.如图2所示.

图2 双点交叉操作示意图

5）变异 变异运算是对个体的某一个或某一些基因座上的基因值按照某一较小的概率进行改变，它也是产生新个体的一种操作方法.本文采用英国设菲尔德大学开发的遗传算法工具箱中mut离散变异算子.变异概率为1／42≈0.02.变异过程如图3所示.

图3 离散变异操作示意图

6）终止代数T 终止代数T是表示遗传算法运行结束条件的一个参数，它表示遗传算法运行到制定的进化代数后就停止运行，并将当前群体中的最佳个体作为所求问题的最优解输出.本文取终止代数为100.

3 实 例

根据前文所列出模型，设某设备的维修项目n＝7，有维修人员m＝6名.维修计划流程图如图1所示，优化的约束条件有：（1）按维修项目的关联次序将维修总耗时的一维时间轴分成若干段，端点为各项目的起点或终点（见图1）；（2）在各个时间段内将维修人员分配给需要开工的维修项目，并且在此时间段内每一个维修人员只从事一个维修项目.维修人员的实时技能矩阵如下.

维修项目 Epj的值为：Epj＝（230，160，330，510，150，290，400）.杂交率Pc＝0.7，变异率Pm＝0.02，初始种群规模取80个.经过100代遗传迭代，得到如下结果：T1＝35.384 6，T2＝40.000，T3＝66.0000，T4＝85.0000，T＝226.384 6.最优的染色体为：Chrom＝［000110 010101101110 000101001100 010101101101］.人员配备如表2所列.

表2即为通过建立模型用遗传算法计算优化所得到的维修人员配备最佳方法.按照此方法对维修人员进行调配，能使维修总工时达到最短.若采用随机人员分配法，例如按随机产生的染色体［000110 011001101110 001010000101111001111110］进行人员分配，则维修总耗时为：T＝328.884 6.由此可见，通过遗传算法优化运算得到人员配备方法极大的缩短了维修总耗时.

表2 维修人员配备图

4 结束语

船舶大修是一项复杂的维修作业，维修项目间存在次序约束，且执行维修任务的人员有限、能力存在差异，合理安排维修人员将直接影响任务完成.根据船舶厂修维修计划建立预定维修次序工作流模型与人力资源能力关系模型，构建人力资源分配策略的优化模型，利用遗传算法找出优化模型的最优解，给出合理的维修人力资源分配策略，以缩短大修时间，从而降低维修费用及船舶停运所造成的损失.

［1］常文兵，肖依永，陈国柱.面向预定维修次序的人力资源分配优化研究［J］.飞机设计，2008（5）：71－75.

［2］刘从虎.多装配线生产车间人力资源优化配置方法及支持系统研究［D］.重庆：重庆大学机械工程学院，2009.

［3］雷英杰.MATLAB遗传算法工具箱及应用［M］.西安：西安电子科技大学出版社，2005.

［4］周 明，孙树栋.遗传算法原理及其应用［M］.北京：国防工业出版社，1999.

［5］Eberhart R C，Shi Y.Particle swarm optimization：developments，applications and resources［J］.Evolutionary Computation，2001，1：81－86.