加筋板在轴向压力下的极限强度研究

张晓丹 杨 平

（武汉理工大学交通学院 武汉 430063）

船体构件的纵向强度极为重要，而加筋板为船舶结构中最为主要的一种结构形式，Paik［1］等对加筋板进行了理论研究；Smith，Faulkner，Tanaka等进行了系列的模型试验；Fujikubo，Paik，Zhang［2］等进行了大量的数值计算并提出了加筋板极限强度计算公式.2006年，IACS共同规范对双壳油船和散货船设计规定了对加筋板的极限强度计算要求.由于船体结构中有大量的加筋板需要进行极限强度计算，若采用有限元程序进行计算，会耗费大量的人力、物力以及时间.本文的工作通过有限元分析软件ANSYS对大量系列加筋板模型进行了非线性有限元数值计算，研究在轴向压力作用下，板的柔度、筋的柔度及边界条件等对加筋板的极限承载能力的影响，并提出一个简便、有效的预报公式，且具有更高精度，为实际船舶结构设计与计算提供便利.

1 非线性有限元计算模型

1.1 计算尺寸

根据对船体加筋板尺寸的统计，加筋板的参数范围如下.

本文对参数在以上范围的Smith及Tanaka＆Endo试验系列加筋板进行非线性有限元计算，将计算结果与实验数据对比分析，研究β，λ的值对加筋板的屈曲和极限强度的影响并归纳简化公式，与Hughes［3］等已发表的多个有限元计算结果对公式做验证和修正.

1.2 加筋板有限元模型

研究中采用有限元分析软件ANSYS对系列计算模型进行非线性有限元数值计算.计算中假定板的材料是理想弹塑性，忽略材料的应力强化作用，以von Mises屈服准则作为材料的屈服准则，材料屈服极限为σy＝315MPa，弹性模量E＝2.058×105MPa，泊松比ν＝0.3.

计算模型取1／2＋1＋1／2个强横梁间距，筋的数目与系列试验加筋板一致，采用文献［4］中提出的约束方式，如图1所示.

图1 计算模型约束方式

即在A－A1，C－C1边施加沿板长度方向对称性约束，加筋板的纵向边界及强横梁处z向简支，在A－C边施加y向约束和在C－C1边施加x向约束限制刚性位移，并在B－B1，D－D1强横梁处，板uz＝0，筋腹板y向位移相同（直边界），以限制筋在强横梁处的侧向变形.由于计算板格取自连续板中的一部分，各边应施加直边界条件，如图中，A－A1施加x方向直边界条件，该截面所有点在受力时x向位移相同；A1－C1边则y向位移相同.

采用shell143单元，单元边长在40～70mm之间.单元数最少2 016个，最多3 328个.取板的一阶屈曲变形作为初始变形，取变形幅值为a／400，并对强横梁腹板所有节点施加约束uy＝0，以限制腹板的侧向位移.不考虑焊接残余应力 .

2 加筋板的极限强度计算

首先，对以下加筋板进行了标定对比计算，结果见表1.

表1 标定计算结果

Tanaka系列1a的初始变形及相应极限状态下的应力分布结果如图2～图3所示.

本文计算的所有加筋板尺寸B＝4b，其他尺寸及计算结果如表2所列.

图2 加筋板初始变形

图3 加筋板极限状态下应力分布

表2 加筋板的尺寸及计算结果

3 公式归纳及误差分析

3.1 公式归纳

通过对50块加筋板的非线性有限元计算，结合Hughes［3］50块板的有限元计算结果，采用数据处理程序DPS对这100组数据进行拟合.目标函数为σu／σv，自变量为β，λ，采用文献［2］的函数形式

将有限元计算所得的以上3个向量代入式（1），用DPS程序对该方程组经过多次近似迭代计算，得出如下公式

经验证，该公式具有较高精度.公式值与有限元计算结果比值分布如图4～图6所示.

图4 本文公式与实验比值关于β的分布

图5 本文公式与实验比值关于λ的分布

图6 本文公式对实验结果的分布

公式值与计算值对比结果及误差如表3所列.其中，13号加筋板屈曲应力的有限元计算值为212.1MPa，屈曲形式为整体屈曲.取此整体屈曲模态为初始变形后，加筋板在压力下发生整体屈曲失效.此时，加筋板板格的极限强度为σu／σy＝2／β－1／β2＝0.709，比加筋板的极限强度值σu／σv＝0.507大，发生整体屈曲，致使加筋板没到达屈服应力而因屈曲失效.

表3 公式值与有限元计算结果

在所计算的100个加筋板数据中，公式值与有限元计算值误差分布如下：45个误差小于5%，43个误差在5%～10%之间，6个误差在10%～15%之间，4个误差在15%～20%之间，1个误差为23.5%.误差分布如图7所示.

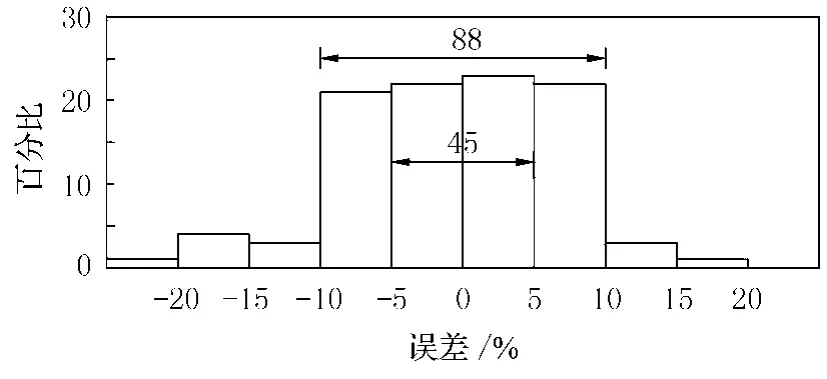
图7 公式与有限元计算误差分布

3.2 本文公式与Paik公式、Zhang公式的比较

以下用文献 ［1］中引用的Tanaka及Smith实验数据及文献［2］中的有限元计算结果来比对三个公式的精度.

Paik［5］公式：

其中，D0A－D4A为Smith实验系列加筋板，1a－4b为Tanaka实验系列加筋板，Z 1－Z 7为文献［2］有限元计算系列加筋板.综合上表可知，Paik公式平均误差为14%，偏离系数COV＝0.32%；Zhang公式平均误差为3%，偏离系数COV＝0.33%，有三个值超过10%；本文公式平均误差为2%，偏离系数COV＝0.32%，所有误差都在10%以内.可见，本文的公式具有较高精度.

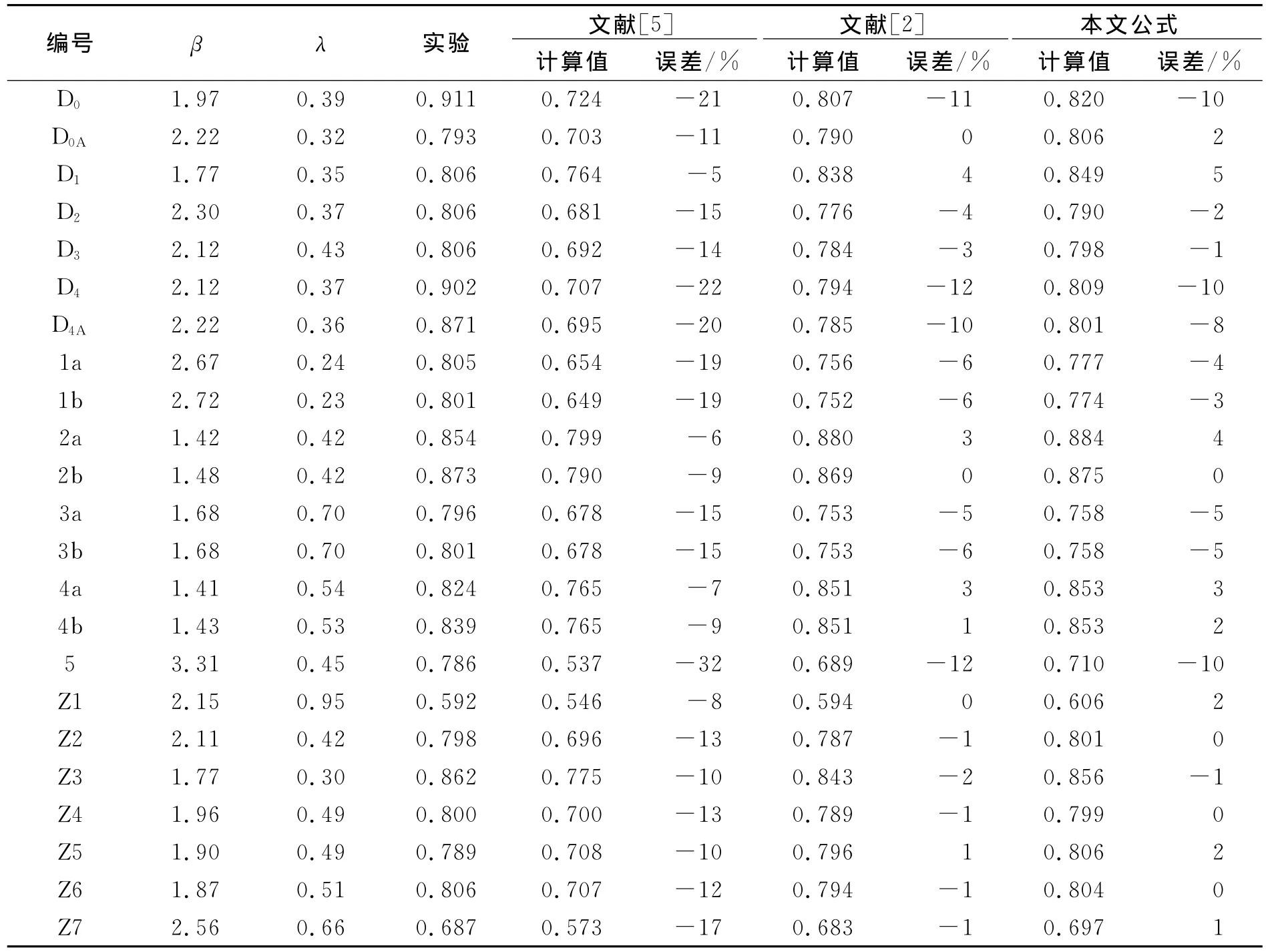
表4 不同公式与试验的误差

4 结 论

1）在提取一阶屈曲模态做为初始变形计算时，加筋板的极限强度不一定比板格的极限强度大，即当

此时加筋板的整体柔度很大，极易发生一阶整体屈曲，致使加筋板没到达屈服应力因变形过大失效.因此，整体屈曲的变形形状及幅值对极限强度结果有很大影响.

从而，加筋板的极限强度（σu／σy）s与板格的极限强度（σu／σy）0之比可以作为设计阶段对加筋板的极限强度优化的目标之一.

2）本文公式与Paik公式、Zhang公式相比具有较高的精度.

本文利用非线性数值计算方法对加筋板在轴向压力下的极限强度进行了非线性分析，结果表明，本文所得公式有较高的精度和实用价值.

［1］Paik J K，Kim B J.Ultimate strength formulations for stiffened panels under combined axial load，inplane bending and lateral pressure：a benchmark study［J］.Thin－Walled Structures，2002，40：45－83.

［2］Zhang S.Buckling and ultimate capability of plates and stiffened panels in axial compression［J］.Marine Structures，2009，22（4）：791－808.

［3］Hughes O E，Ghosh B，Chen Y.Improved prediction of simultaneous local and overall buckling of stiffened panels［J］.Thin－Walled Structures.2004，42：827－856.

［4］ISSC.Ultimate Strength.Proc.of 17th international ship and offshore structures congress［C］／／Korea，2009：377－474.

［5］Paik J K，Mansour A E.A simple formulation for predicting the ultimate strength of ships［J］.Journal of Marine Science and Technology，1995（1）：52－62.