舰船物资转运方案计算机辅助决策算法研究

张晓东 童 剑 郭 敏 黄祥钊

1海军装备部 舰船办公室，北京100071 2中国舰船研究设计中心，湖北武汉430064 3华中科技大学 系统工程研究所，湖北 武汉430074

舰船物资转运方案计算机辅助决策算法研究

张晓东1童 剑2郭 敏3黄祥钊2

1海军装备部 舰船办公室，北京100071 2中国舰船研究设计中心，湖北武汉430064 3华中科技大学 系统工程研究所，湖北 武汉430074

瞬息万变的现代战场对大中型水面战斗舰船甲板物资转运的效率提出越来越高的要求。引入计算机辅助决策技术，在考虑多种牵制因素的情况下，快速获得最优的物资转运方案。详细分析和阐述舰船物资转运线路规划、时间计算、作业排序以及资源配班等4个主要问题的计算机解决方法，为利用计算机辅助制定最优物资转运方案提供可行途径。

线路规划；转运作业时序；资源配班；转运方案；决策支持

1 引言

现代大中型水面战斗舰船由于作战使命任务的需要，携带有大量战斗和生活物资，并且在远海作战时还需要中途大量补给物资。各类置于甲板上的战斗物资包括弹药以及加满燃油的飞机等都具有较高危险性，如果这些物资长时间暴露于甲板或不能快速调整舰载武器的布置状态备战，舰船随时会成为敌方攻击的目标。因此，甲板面的各类战斗物资不仅需要安全转运，更需要高效转运［1－3］。

关于舰船物资转运，国内相关的研究成果虽然较多，但对物体运动的转角限制以及物体并行运动的最优时序等影响实际作业执行效率的重要问题却考虑较少，因此研究成果在实际应用中的可操作性略显欠缺。本文通过对舰面物资转运作业路径规划、时间计算、作业排序以及多作业并发下的转运资源的配班设计等研究，探索利用计算机技术为大中型舰船舰面物资安全、高效的调配和转运作业制定规划方案的可行解决途径，从而为相关指挥人员提供便捷的辅助决策手段。目前基于本文所提方法而开发的软件已得到了实际应用，效果良好。

2 物资转运线路规划

物资转运的首要问题是转运线路的规划。相对于大型物资如批量运送的弹药以及飞机等而言，舰船甲板面积较小，因此在物资转运的路径规划方面不能单纯将此类物资视为质点考虑其运送路线，而应该结合考虑各类物资的不规则外部轮廓，从而在路径规划上避免物资与物资之间、物资与船体结构之间发生碰撞，并在此基础上充分考虑运送车辆的轮转角渐变特性，建立数学模型，研究适合于舰船物资转运的路径搜索算法和策略。

2.1 物体外形的表示方法

舰船上的物资通常由专用转运车转运。物资或码放在车上（如弹药等），或由转运车牵引（如飞机等）。如果由转运车托运，则说明物资的体积较车小，可将车的外形作为转运物资的外部轮廓，而如果由转运车牵引，则说明物资的体积较车大，此时可直接考虑被牵引物资的外形轮廓。鉴于大型舰船甲板面用于人员和物资转运活动的区域一般较为平整，甲板上的凸出物不会对车辆和物资转运作业的安全构成威胁，因此可以仅从俯视角度下的二维平面分析物体之间的相对位置。

二维平面中物资外形的表示方法，是将物体的俯视投影面上的外沿轮廓线转换成一系列节点坐标。节点的数量根据物体外形的不规则程度确定，一般轮廓曲线较少的物体其轮廓节点也少，而轮廓曲线复杂的物体完整表达的其轮廓节点数量将非常庞大。较小的数据量有利于提高下文提及的线路规划运算效率。为尽可能在减少表征物体外沿轮廓数据量的同时，能够近似完整地表达物体外部轮廓，可将物体复杂的外沿轮廓曲线近似划分为多条直线段的组合，从而使该物体表征为若干多边形的组合。

2.2 物体姿态的表示方法

舰上物资在转运过程中，很少有呈圆形的俯视投影面，因此物体在运动过程中将呈现出不同的姿态；而不同的姿态下物体所占用的甲板空间以及与周围物体的距离都不同，转运线路的设计将必然不同，因此需要将物体在二维平面上的姿态和指向转换成数字描述方式。物体在甲板上的姿态主要体现在与舰船纵轴线的夹角变化，而要将这一特性转换为数学语言，必需进行角度数值的离散化，即在360°连续的角度数值中选择若干个角度，则转运物资的任意姿态均能按照相应的门限进行归并处理，从而使姿态角度的变化具备利用计算机进行计算处理的条件。图1为按照45°的精度将360°划分为8个区间的示例，在该精度条件下，计算机所能识别的物资姿态角度为8种。

图1 物体姿态角的定义Fig.1 Definition of posture angle for an object

2.3 舰船甲板转运空间的表示方法

由于物资的转运作业以大中型舰船的甲板面为背景，因此需要将舰船甲板面也表示成一系列数值。下面以甲板轮廓是矩形为例，以舰纵向为x轴，舰横向为y轴构建直角坐标系，将甲板平面划分成m×n个正方形栅格 （m行，n列），从而利用（m＋1）×（n＋1）个点坐标表示出甲板面。在栅格图中，每个栅格分为两种情况：一是自由栅格点，栅格属于自由空间，即转运物资轮廓曲线可以进入的空间；二是障碍物栅格点，属于障碍物空间，这些栅格点上不允许转运物资轮廓曲线进入。图2为m=70、n=32时，矩形轮廓甲板面的栅格点示意图。

图2 空间网格的定义Fig.2 Schematic of space grid

2.4 转运线路规划算法的基本原理

根据物体转运车辆的运动约束条件，在全部转运作业空间栅格中生成物体的一步转移网格［4－5］，如图3。根据机器人运动规划原理［6－7］，从某个网格节点A出发，按照一定步长，一步可以达到下列节点：

图3 物资一步转移网格图Fig.3 Material transfer meshes

其中F2为物体的几何中心点所在位置沿着姿态角方向前进所能到达的目标栅格点，B2为沿着姿态角方向后退所能到达的目标栅格点，F1为沿着左圆方向弧线前进所能到达的目标栅格点，B1为沿着左圆方向弧线后退所能到达的目标栅格点，F3为沿着右圆方向弧线前进所能到达的目标栅格点，B3为沿着右圆方向弧线后退所能到达的目标栅格点。物体每走微小的一步（称为一个步长）都选择其中的一条路径，那么从起始点（起始点坐标和姿态角）到终止点 （终止点坐标和姿态角）的任意一条可行路径都可以表示为一系列圆弧和直线的组合。

目前有很多求解最短路的算法［8－10］。比如Dijkstra、Flod以及A*、D*算法［11］等等，但是这些算法由于遍历计算的节点很多，当栅格空间节点非常多的情况下，计算时间往往不能满足调运的实时性要求。因此针对本问题，我们主要结合遗传算法来进行线路规划。遗传算法是由Holand在60年代提出的一种以自然遗传机制和自然选择等生物进化理论为基础的随机化搜索算法，其优越性表现在：1）在搜索过程中不易陷入局部最优，即使在适应度函数不连续、不规则、有噪声的情况下也能以较大的概率找到全局最优解；2）采用自然进化机制来表现复杂的现象，能快速解决较困难的问题，易于介入已有的模型，扩展性强。

利用遗传算法求解该路径问题的基本思路是：在转运全局地图的基础上，产生一组从起始点至目标点的由若干中途点组成的初始种群，再按适应度的大小选择个体，并进行复制、交叉和变异等遗传操作，从而产生出代表新的解集的群体，如此往复，逐代演化产生出越来越好的近似解。整个过程将导致种群像自然进化一样，后代种群比前代具有更短的线路长度，因此末代种群中的最优个体经过解码（从基因到性状的映射），可以作为问题近似最优解。

3 物资转运时间计算

物资在转运线路上的移动可以分为两类：一是物资通过升降平台进行转运，这类操作的执行时间相对固定，主要由升降平台的运行指标决定；二是物资在甲板上的转运，这类操作的执行时间影响因素较为复杂，主要有转运线路的长度（距离影响）、途中的转弯弧度（速度影响）、线路周边的空闲空间大小（速度影响）以及转运车驾驶员的熟练程度（速度影响）等。其中线路周边的空闲空间影响转运速度是由于当周围转运空间较小时，为了保证物资的运输安全，转运车将以较低的速度通过，而当空间较为宽敞时，则可以较快的速度通过。

为了较为精确地拟合计算出物体在转运线路上所花费的时间，可以根据问题的实际背景，将转运线路中第n个节点和第n＋1个节点之间的转角分成L个等级表示。例如将360°角划分为12份，即30°为一个等级（可以再细化，细化程度根据数据量大小和运算速度决定），则以0°、30°、60°、90°……的顺序逐级递增，其转角对应着不同的加权系数Zi（i＝1，2，…，12），其中0≤Zi≤1（一般转运车不能横向移动，则当转角为90°时，Zi＝0；直线运行时速度最大，则当转角为0°时，Zi＝1），同理将线路周围空闲空间大小按照间隔距离也划分出相应等级，例如以50 mm为一档将最短间隔距离划分为300 mm、350 mm、400 mm、450 mm……m个等级，则同样每个等级范围内的最短距离对应着不同的加权系数Ji（i＝1，2，…，m），其中0≤Ji≤1（当周围空间非常拥挤，对转运车驾驶员安全转运物资构成极大心理压力，如最近的物体间隔正处在安全转运的最小规定门限值时，如300 mm，则Ji＝0；当周围空间较大，对转运车驾驶员安全转运物资不构成任何心理压力，如最近的物体间隔为5～10 m，则Ji＝1）。

如图4所示的一段转运线路，按照不同的转弯半径分为3段，每段线路长为li（i＝1，2，3），考虑到转弯半径和周围空间对转运车速度的影响，转运车在每段线路上运行的速度分别为v×Zi×Ji（i＝1，2，3，0≤Zi≤1，0≤Ji≤1，V表示转运车额定负载状态下的限定车速），则该段线路上总的转运时间可有如下表示：T＝l1／（V×Z1×J1）＋l2／（V× Z2×J2）＋l3／（V×Z3×J3）。

假设图4中l1＝10 m，l2＝5 m，l3＝20 m，转运车直行速度为1 m／s，根据图4中l1和l2的转角变化率对比情况，设定转角加权系数Z1＝0.5，Z2＝0.3，而Z3＝1，再设定本段线路周围没有其他物体，则最短距离加权系数J1＝J2＝J3＝1，则按上述公式本段线路的转运时间应为：T≈56.7 s。

由于转运线路的长度、转角以及与周围物体的间隔距离等特征参数均可由上节中的方法得出，因此舰船甲板面上任何物资的转运时间均可依本节所述方法近似得出。当然，为了使计算出的运行时间更趋近于真实情况，还应结合大量实践操作得出作业时间的统计数据，并在此基础上对相关加权系数Zi和Ji的取值进行调整。

图4 转运线路的分段表示Fig.4 Schema of a transfer path

4 物资转运排序规则

多件物资的转运作业必须是有序进行，而次序的排列需要按照一定的规则。如欲转运物资的原始位置正处在其他需转运物资的转运路线上，则应先调移该物资；又如某物资的转运目的地处在其他需转运物资的转运路线上时该物资应后调动等等。为了提高作业效率，舰船上一次要执行多种物资的转运工作，因此必须综合考虑所有物资的转运线路才能得出正确的排序方案。

下面首先以两件物资转运线路之间的关系对物资的转运次序进行研究，然后以一种3件物资转运的情况为例进行方法适用性分析。

4.1 两条线路在描述上基本重合

主要分为以下两种情况：

1）A物体的起始位置处在B物体的转运线路上，而B物体的目标位置处在A物体的转运线路上，则B物体可以随A物体一起移动完成转运，如图5a所示。

2）A物体的起始位置处在B物体的转运线路上，而其目标位置也处在B物体的转运线路上。该情况下A物体必须先移动，B物体才能移动，但又不允许A物体先到达目的地，否则会堵塞B物体的转运线路。因此A物体需要采取避让性的转运操作，即将其移动到附近某个空闲位置暂留，待B物体通过A物体初始位置后再返回原位置进行转运。如图5b所示。

图5 两物体转运线路在描述上基本重合Fig.5 Two transfer paths in the same way

4.2 转运线路在描述上不完全重合

4.2.1 转运线路中段在描述上不重合

转运线路中段又分两种情况：

1）A、B物体的转运线路中段代号分别为X、Y。由于A物体起始位置处在B物体的转运线路上，因此A物体应先于B物体经过n点移动到X段或Y段，并且先于B物体经过O点才能保证转运任务的完成。如图6a所示。

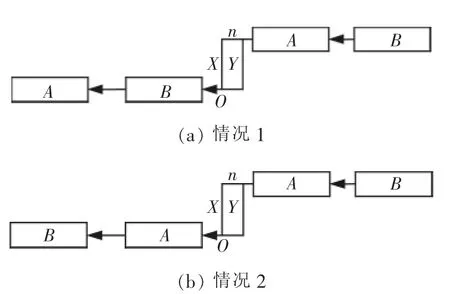
图5 两物体转运线路中段不重合Fig.5 Two transfer paths different in central part

2）A物体的起始位置和目的地同处在B物体的转运线路上，与4.1节2）中的情况相似，但由于中段线路不同，A物体不必采取特殊的避让性调运操作，可先移动通过n点到X段，B再移动到Y段，而在O点处应保证B物体先于A物体通过则能完成转运。如图6b所示。

4.2.2 转运线路起始段在描述上不重合

A物体和B物体的起始位置均不处在另一方的转运线路上，但B物体的目标位置处在A物体的转运线路上。A物体需先调运经过交点O到达目的地，B物体才能完成转运。如图7所示。

图7 两条转运线路起始段在描述上不重合Fig.7 Two transfer paths different at the beginning part

4.2.3 转运线路目标段在描述上不重合

A物体和B物体的目的地均不处在另一方的转运线路上，但A物体的起始位置处在B物体的转运线路上。A物体需先调运通过交点O，B物体才能完成转运，如图8所示。

图8 两条转运线路目标段在描述上不重合Fig.8 Two transfer paths different at the ending part

4.3 转运线路在描述上不重合但相交

A物体和B物体的转运线路仅在某处会使用相同的资源。该情况下A、B两物体可同时移动，在交点O处协调通过，如图9所示。

图9 两条转运线路目标段在描述上不重合但相交Fig.9 Two transfer paths different but cross each other

4.4 转运线路在描述上不相交

A物体和B物体的转运线路具有互异性，在这种情况下两物体的调运次序是任意的，如图10所示。

图10 两条转运线路目标段在描述上不相交Fig.10 Two transfer paths totally different

4.5 3件物资转运示例

以上是两件物资转运线路之间所有可能的关系，并对每种关系下转运作业的先后次序进行了分析，这是多件物资转运作业次序研究的理论基础。下面以3件物资的转运为例说明如何使用上述研究结果得出相应的转运次序。

如图11所示，对A、B、C 3件物资的转运线路分别为：A线路n－m－X－o－A，B线路A－n－Y－o－A－B，C线路m－X－o－A－C。其中A物体与B物体的调运线路关系属于上面分析的4.2.1节中的第2种情况，依据上面得出的结论，A物体应先移动通过n点到X段，而在O点处应保证B物体先于A物体通过；A物体与C物体的转运线路关系属于4.2.1节分析的第2种情况，依据结论，C物体需先调运经过m点和O点到达目标站位；B物体与C物体的转运线路关系属于4.3节分析过情况，则依结论B、C两物体可同时移动，在A的目标位置上协调通过。

图11 3件物资的转运线路示例图Fig.11 A demonstration for three transfer paths

按照上述分析，在A物体与B物体之间，A物体先移动，在A物体与C物体之间，C物体先移动，则3件物资的转运次序为C、A、B。在对调运作业的具体过程进行分析时上述的3种线路关系所得出的结论都应该是被满足的，因此有：C物体先于A物体经过m点，A物体先于B物体经过n点，B、C两物体可不分先后但均先于A物体通过O点完成调运。由此可见，多件物体的转运顺序可以通过这些物体经过一些特殊交点的先后次序表达。因此，可以将上述两件物资在各种情况下的转运顺序建成基础规则库，进而解决更多物资同时转运的计算机辅助排序问题。

5 物资转运资源配班

根据上述转运线路规划、转运时间计算以及转运排序规则所阐述的原理，利用计算机可以列举出各种先后顺序下的多件物资转运的作业时序，但所有的时序还只是考虑了物资转运空间上的干涉问题，而要使作业时序具有实际可行性，还需结合转运资源如转运车辆以及人员班组的数量、状态及位置等具体情况对作业时序进行配班筛选，从而获得转运总时间最短或者所需资源最省的转运方案。由于转运车辆和人员班组的配班属于同类问题，因此本文主要阐述转运车辆的配班设计思路。

如上所述，物资转运线路、作业时段各有不同，因此需要针对这些特点考察转运车辆是否能按照线路规划得出的作业时序在规定的时间到达指定物资附近，并选取能够及时到达的车辆进行配班和作业时长的比较。

转运车配班设计的基本思路是：

1）针对作业时序S中最早转运的物资n，配置转运车P；

2）以物资n结束转运的时间为基准，以转运车移动时间为限制条件，在后续转运物资n＋i（i＝1，2，3，…）中寻找可以继续使用转运车P的物资m；

3）如果存在若干件物资m，则选取这些物资中开始转运时间距离物资1结束转运时间最近的物资X，为其配置转运车P；

4）以物资X结束转运的时间为基准，循环执行上述2）、3）项，直至遍历不到物资m为止，得出可供配置转运车P的全部物资项；

5）为尚未配置转运车中最早转运的物资配置转运车P＋1；

6）循环执行上述2）～5），直至全部转运车已分配完；

7）如果此时所有物资均分配到了转运车，则将作业时序S的配班结果保存为转运作业方案Z，否则由于转运资源不能满足要求，作业时序S被舍弃；

8）针对作业时序S＋1，执行1）～7）项，将获得的配班结果保存为转运作业方案Z＋1，依此思路直至将线路规划算法计算得出的全部作业时序组合遍历完毕；

9）在最终得到的全部转运作业方案中，找出转运总时间最小的方案和转运车使用台数最省的方案。

下面针对具体情况进行举例分析说明：

假设：

1）舰船上有4件物资需要转运，初始位置和目的地见表1（表中Fi和Ji分别指上层甲板和下层甲板中的任意几点位置）。

表1 物资转运情况示例表Tab.1 Example list for object transfer

2）舰船用于物资转运的升降平台共有前后两部，且初始时均处于上层甲板。升降平台上升（或下降）所用时间设为QS；

3）转运车共有A、B、C、D 4台，A、B车负责上层甲板的物资转运，C、D车负责下层甲板仓库的物资转运，两层甲板间车辆不跨层使用；

4）转运车从上层甲板上任意位置Fn（n＝1，2，3，4）到前升降平台的时间设为QTn（n＝1，2，3，4），到后升降平台的时间为HTn（n＝1，2，3，4），从前升降平台到后升降平台的时间为QH；转运车辆从下层甲板仓库中任意位置Jn（n＝1，2，3，4）到前升降平台的时间为qtn（n＝1，2，3，4），到后升降平台的时间为htn（n＝1，2，3，4），从前升降平台到后升降平台的时间为qh；

5）在不考虑转运车辆的前提下由线路规划算法得出的某种线路时序如图12所示，其中iM0表示物资i（i＝1，2，3，4）开始转运的时间，iM1表示物资在上层甲板上转运结束的时间，iM2表示物资完成升降平台转运的时间，iM3表示物资完成仓库内转运的时间。

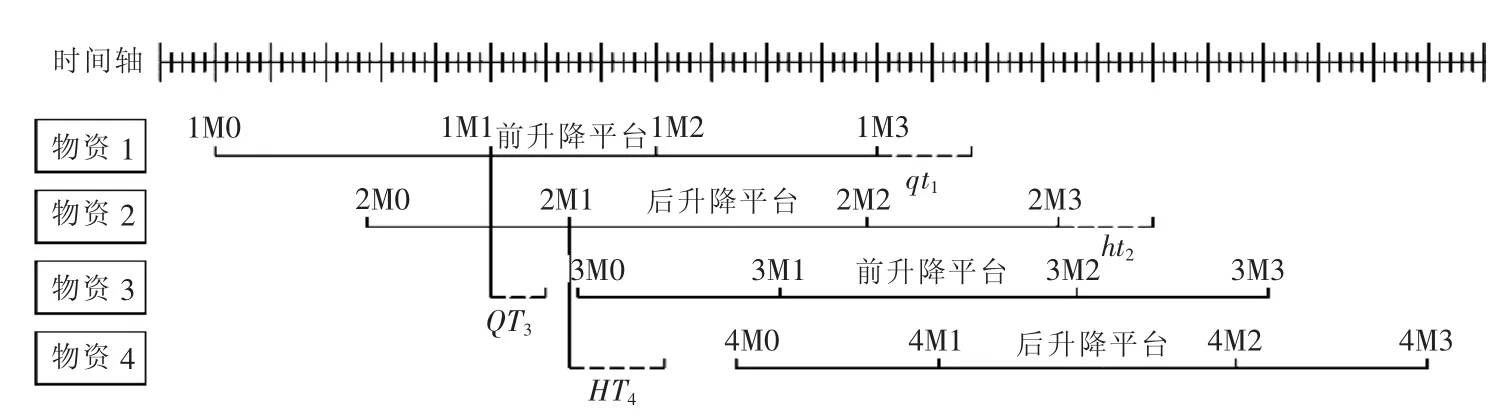
图12 物资转运作业时序图Fig.12 Operation timing diagrams

则上述转运车配班设计思路的具体实现如下：

1）上层甲板为物资1配置转运车A，下层甲板仓库为物资1配置转运车C；

2）由于2M0＜1M1、2M2＜1M3，说明物资2在上层甲板此时无法配置转运车A，下层甲板仓库此时也无法配置转运车C；

3）由于3M0－1M1≥QT3、3M2－1M3≥qt1，且物资3在上层甲板和下层甲板开始转运的时间都距离物资1结束的时间最近，因此可为物资3在上层甲板配置转运车A，下层甲板仓库配置转运车C；

4）接着以物资3作为基准，对物资4的转运车配班进行分析。由于4M0＜3M1、4M2＜3M3，说明物资4在上层甲板。此时无法配置转运车A，下层甲板仓库此时也无法配置转运车C；

5）在结束物资1～4的第一轮转运车配班筛选后，剩余物资2和4未完成配班，引入转运车B、D进行配班：在上层甲板为物资2配置转运车B，下层甲板仓库为物资2配置转运车D；

6）由于4M0－2M1≥HT4、4M2－2M3≥ht2，可为物资4在上层甲板配置转运车B，下层甲板仓库配置转运车D；

7）完成在该时序下的转运作业方案。

通过此例，说明了该配班算法思路可以作为通过舰船物资转运时序进一步生成转运方案的可行方法。

6 结论

本文阐述将计算机辅助决策技术应用在大中型舰船甲板物资转运领域并获得最优作业方案的基本思路，详细分析了为不规则外形物体计算无碰撞干涉转运线路的算法思路，以及在此基础上以加权系数的方式将转运线路的实现难易结合进转运作业时间的计算中；再针对物资转运线路与其转运顺序之间的关系进行梳理分析，获得转运作业时序排列的重要算法规则；最后将舰船上配置的转运资源与每种转运作业时序进行匹配，从而得到满足资源条件的情况下耗时最短的转运方案和转运资源使用最省的方案。

通过对舰船物资转运方案的计算机辅助决策算法思路的研究，基本理清了针对该问题的算法研究思路，但还存在以下几点问题需要进一步开展研究：

1）通过物资转运线路规划算法得出的线路结果一般用细密的栅格节点连成的曲线表示，而通常在舰船甲板上这些栅格节点并不存在，因此目前转运车驾驶员只能粗略按照规划线路驱动转运车，将影响后续得出的优化转运方案的实际作业效果。如何使转运车能精确地按照指定的线路运送物资，还需通过开展相关转运线路指示技术的研究以保证转运方案的最优实施效果得以充分发挥；

2）物资转运时间计算的算法原理虽较为简单，但相关时间参数特别是加权系数的设置对转运时间的准确性有着至关重要的影响，而转运作业时间的准确程度又直接关系到后续作业排序以及配班设计的结果。因为转运车及班组的配班要满足线路时序图的要求，必须避免其在规定的时间内无法到达指定目的地的情况；而如果这些计算得出的时间与真实操作所需花费的时间存在较大差别，则配班算法得出的最优方案甚至在实际作业中不具有可行性，这样的结果将使决策算法得出的最优方案完全尚失对现实操作的指导意义。因此，必须在严格依照设备相关运行性能指标进行分析计算的前提下，通过开展实操试验对相关参数进行不断的修正 （相关参数应为可更改的输入变量），以使得理论计算与实际运行的时间尽可能趋于一致。

［1］刘亚杰，王航宇，谢君.调运问题中基于栅格模型的快速路径规划方法［J］.海军工程大学学报，2009，21（1）：87－90.

［2］马登武，郭小威，吕晓峰.基于网络计划技术的舰载机航空导弹转运流程［J］.兵工自动化，2010，29（9）：48－51.

［3］杨炳恒，王海东，韩峰，等.舰载机调运作业流程优化研究［J］.科学技术与工程，2010，10（22）：5602－5605.

［4］王红卫，马勇，谢勇，等.基于平滑A*算法的移动机器人路径规划 ［J］.同济大学学报 （自然科学版），2010，38（11）：1647－1650，1655.

［5］刘亚杰，王航宇，谢君.狭窄环境中基于几何法的全局路径规划新方法［J］.海军工程大学学报，2010，22（4）：82－86.

［6］温瑞，王航宇，谢君.一种移动机器人路径规划方法［J］.兵工自动化，2009，28（12）：60－63.

［7］吴海彬，林宜.基于改进Voronoi图的移动机器人在线路径规划［J］.中国工程机械学报，2007，5（1）：117－121.

［8］ERINC G.Nonholonomic motion planning with genetic algorithms for car－like robots［D］.Bremen：International University of Bremen，2006.

［9］张洪宁，张鹏程，刘春明，等.基于动力学模型的轮式移动机器人运动控制［J］.兵工自动化，2008，27（11）：79－82.

［10］PLAKU E，KAVRAKI L E，VARDI M Y.Discrete search leading continuous exploration for kinodynamic motion planning ［C］//Robotics：Science and Systems.Atlanta，Georgia，2007.

［11］NASH A，DANIEL K，KOENIG S，et al.Theta*：Any－angle path planning on grids［C］//Pproceedings of the National Conference on Artificial Intelligence（AAAI）.AAAI Press，2007：1177－1183.

Computer Aided Decision-Making Method for Material Transfer Planning on Ship Deck

Zhang Xiao－dong1Tong Jian2Guo Min3Huang Xiang－zhao2
1 Ship Division，Naval Armament Department of PLAN，Beijing 100071，China 2 China Ship Development and Design Center，Wuhan 430064，China 3 Huazhong University of Science and Technology，Wuhan 430074，China

Modern battlefield requests faster and faster deck material transfer on the large warship.We made use of computer-aided design technology to solve the problem of optimizing ship deck material transfer scheme，considering multi－factors that affect the result of a naval warfare.We discussed and analyzed the method about computer-aided ship deck material transfer planning，and explained the strategy in detail about how to plan transferred paths，calculate task time，sequence，resource partnership and so on.

paths planning；task sequence；resource partnership；transfer planning；decision-making support

TP242，O22

：A

：1673－3185（2011）04－104－07

2011-05-06

张晓东（1971－），男，硕士，工程师。研究方向：航空保障装备研制。E-mail：haijun_zxd＠163.com

童 剑（1979－），男，硕士，工程师。研究方向：智能机械及自动化。E-mail：childsword＠163.com

郭 敏（1969－），男，博士，副教授。研究方向：供应链管理、证据推理理论、仿真、建模与优化。E-mail：guomin＠mail.hust.edu.cn

10.3969/j.issn.1673-3185.2011.04.023