基于改进型模糊层次分析法的舰艇生命力评估

刘晋祥 金 涛

海军工程大学 舰艇安全技术系，湖北武汉430033

基于改进型模糊层次分析法的舰艇生命力评估

刘晋祥 金 涛

海军工程大学 舰艇安全技术系，湖北武汉430033

由于舰艇系统的复杂性，对全舰进行生命力评估需要将其分解到下一级或几级具体的子系统，通过系统生命力指标得到全舰生命力的描述。传统的模糊层次分析法（FAHP）存在两个缺陷：一方面可能导致计算结果错误；另一方面也可能造成无法计算指标权重，使模糊层次分析法的使用范围受到限制。采用一种改进的模糊层次分析法，建立三角模糊判断矩阵，确定各层次间相关因素的权重，并计算得到各子系统的权重排序。实例证明，该模型的评估结果反映了舰船系统的实际工况。根据该模型计算的评估结果，可以更好地发现舰艇生命力系统的薄弱环节，为损管决策提供科学的理论依据和方法。

舰船生命力；评估；模糊层次分析法；损管决策

1 引言

舰艇抵抗各种破损灾害，能够最大限度地保持和恢复其航行和作战的能力，称为 “舰艇生命力”。舰艇是一个综合性的系统，随着现代科学技术的发展，现代海战的立体性、突然性、杀伤性、快速性的日益增强，舰艇的生命力必须随着舰艇的攻击能力协调发展［1］。因此，生命力的评估已经越来越受到人们的广泛关注。

由于舰艇系统的复杂性，要对全舰直接进行生命力的评估是不现实的。这就需要将全舰生命力分解到其下一级或者几级可具体操作的子系统中，通过下级子系统的生命力指标得到全舰的生命力描述。而层次分析法［2］就是在此基础上，形成的一种以评价方案和指标的重要性相互比较为基础，通过判断矩阵可以将定性分析和定量分析有机结合起来的方法。由于它的模型简单、层次清晰，在进行大型水面舰艇的生命力评估时，仍然用于系统模型构建和分析上，成为了生命力评估的一种不可缺少的方法［3］。

但是，或者各指标难于量化，或者一致性的约束很难达到，在很多情况下我们并不能很好地给出指标权重，因此层次分析法的实用程度并不高。我们把模糊数学的概念引入到层次分析法（AHP）的判断矩阵构造中，在充分考虑到人为判断模糊的前提下，使判断矩阵更加合理，这就是模糊层次分析法［5－7］。目前，国内外已有不少研究人员探讨了模糊层次分析法在各个领域中的应用，并取得一定的成果［8－10］，但是在生命力评估领域尚属空白。本文重点介绍了一种改进型模糊层次分析法［4］，并将方法运用到舰艇的生命力评估。

2 三角模糊数的基本概念

采用由Satty提出的层次分析法在确定同层次两相对元素的重要性时，经常面对不确定或模糊的情况，这时，原来构建的标度矩阵就会有偏离实际的情况。鉴于此，将三角模糊数的概念引入到该方法中，用以确定权重。三角模糊数的定义如下：

令A＝（aij）n×n表示由三角模糊数组成的模糊判断矩阵。其中aij＝（lij，mij，uij）。如果lij，uij为左右扩展，表示判断的模糊程度；mij反映指标i比j的重要程度。i与j的相互判断可采用与层次分析类似1～9标度的打分规则，如表1所示。对于aji而言，有aji＝1／uij，mji＝1／mij，uji＝1／lij。

每个模糊判断矩阵的元素aij都有一个模糊评判区间：eij＝uij－lij。该区间反映了专家评判结果的可信度，从某种意义上可理解为数理统计上的“置信区间”。eij越小，可信度越大；反之，eij越大，可信度越小。

表1 标度值及其含义Tab.1 Meaning of the scale

给出三角模糊数的有关运算法则：令M1＝

3 基于三角模糊数的改进型层次分析法

3.1 建立三角模糊判断矩阵

判断矩阵是描述针对上一层某个元素，本层与其有关联的元素之间相互重要性的比较。它是由有经验的专家通过客观判断，依据层次分析法中事前规定的标度进行定量化。利用三角模糊数可得到表示决策者对比较元素相对重要性的模糊判断矩阵。

假设对一指定的决策指标，与其有关联的元素有n个，共有t个专家比较各元素之间对指标的重要程度并进行打分，组成了一个“综合”的模糊评判矩阵R，每个元素rij最多有t个模糊数（即允许决策者对某些方案间的两两比较判断不作表态）。那么必须对这个矩阵进行处理，以便消除专家因为个人偏好对打分的影响。根据三角模糊加法运算法则，求得指标模糊判断的平均值：

另外，由于矩阵具有互反性质，在实际的打分过程中。只要打出上三角（或者下三角）的元素，下三角 （或者上三角）的元素可以通过性质计算得到。实际的判断矩阵具有以下形式：

3.2 构造模糊评判因子矩阵E

传统的模糊层次分析法存在的2个缺陷［4］：一方面可能导致计算结果错误；另一方面也可能造成无法计算指标权重，从而使模糊层次分析法的使用范围受到限制。因此，将可信度引入到普通判断矩阵中，这样既可以消除传统方法的2个缺陷，又可以反映判断专家的“不确定性”对评判结果的影响。由于专家的客观判断有一定的模糊性，为了减少因此产生的误差，可以构造评判因子矩阵E：

3.3 计算调整判断矩阵Q

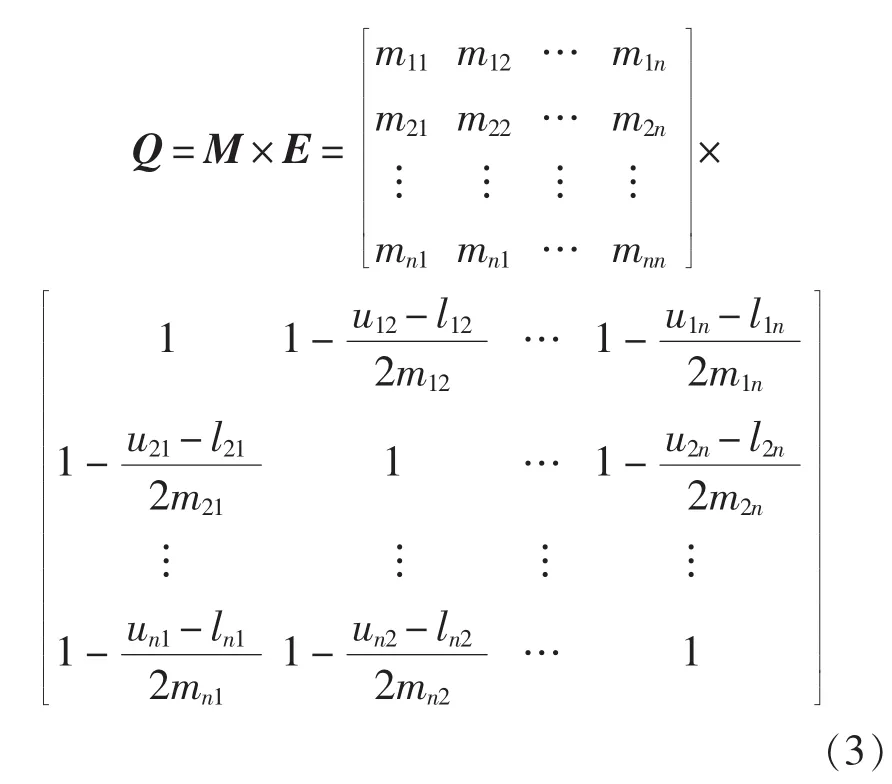
并调整判断矩阵Q，按列转换为对角线为1的判断矩阵Q′。

3.4 层次单排序

利用方根法计算指标i对应的权重：第一步，Q′的元素按行相乘；第二步，所得到的乘积分别开n次方；第三步，将方根向量归一化记得排序权重向量。

即有：

3.5 层次总排序

计算同一层所有元素对最高层（目标层）的相对重要性的排序权值即为层次总排序。设在第1层所有元素A1，A2，…，An相对于目标层的权重为α1，α2，…，αn。在第2个层次中，m个元素B1，B2，…，Bm相对于第1层次的第i准则Ai（i＝1，2，…，n）的权重分别为βi1，βi2，…，βim。则第2个层次m个因素相对于目标层权重为φi＝αi*βij。以此类推，便可得到所有元素相对于目标层的排序权重，从而实现了所有底层因素的重要性排序。

4 应用举例

根据全舰生命力系统的划分，以及对生命力的影响，把全舰生命力层次结构设置为如图1所示。在图1中，把全舰生命力设计为1个3个层次的结构模式，目标层A为全舰生命力系统，中间层B为影响目标层的主要因素，最底层C为待求权重排序的与中间层B相关的子系统。

4.1 根据专家打分构造三角模糊评判矩阵

层次结构建立之后，选取本领域的有经验的3位专家对其打分，得到三角模糊评判矩阵。限于文章篇幅，这里只给出系统B层次结构之间的判断矩阵。

图1 全舰生命力系统逻辑结构图Fig.1 Logical structure of the ship survivability system

4.2 层次单排序

下面以B1，B2，B3，B4为例，介绍层次单排序的方法。按照如下步骤即可得到B层各个系统之间的权重。

表2化简得到平均模糊矩阵为：

表2 B1，B2，B3，B4三角模糊数判断矩阵Tab.2 Judgement matrix of the B level based on triangle fuzzy number

根据式（2），得到模糊因子评判矩阵：

根据式（3），得到调整判断矩阵：

利用方根法，得到元素的对应权重分别为：

α1＝0.406，α2＝0.118，α3＝0.177，α4＝0.299经检验结果满足一致性要求。

重复上面的步骤，计算各层相对上层的权重，可得：破损稳性C11、破损浮性C12、破损强度C13、损管系统C14相对于平台完整性及保障系统B1的权重分别为0.359，0.313，0.207，0.121；操船系统C21、推进系统C22、辅助系统C23相对于机动性系统B2的权重分别为 0.212，0.603，0.195；发电系统C31、供电系统C32、用电系统C33相对于电力系统B3的权重分别为0.692，0.245，0.063；对海作战系统C41、对空作战系统C42，对潜作战系统C43、电子对抗系统C44、通信导航系统C45相对于作战系统B4的权重分别为0.387，0.232，0.224，0.087，0.07。

4.3 层次总排序

根据公式φi＝αi*βij，计算得到表3所示结果。

通过表3可以看出，平台完整性及保障系统是全舰的基础，是整个系统中最重要的部分；维持舰船破损时的稳性和浮性是保持全舰生命力的前提。在此之上，发电系统以及（对海）作战系统具备一定的工作状态同样重要。权重排序为舰艇指挥员在战斗中发生综合性损害时做出正确的损管决策提供了依据。

表3 全舰生命力系统的综合评估结果Tab.3 Consequences of the assessment on ship survivability system

5 结论

基于模糊层次分析法的舰艇生命力评估模型中，以三角模糊数表示不同指标的相对权重比用确定的实数表示更符合人的判断习惯。该方法将层次分析法扩充到模糊环境中，降低了权重系数的人为主观性，提高了评估结果的容错能力。通过实例证明，该模型的评价结果符合舰船系统的实际工况。另外，根据该模型计算出的评估结果，可以更好地发现舰艇生命力系统的薄弱环节。

［1］浦金云.舰船生命力论证［M］.武汉：海军工程大学，1991.

［2］许树柏.层次分析法原理［M］.天津：天津大学出版社，1988.

［3］尹曰建，浦金云.现代作战舰艇生命力的层次分析法综合评估［J］.长春工业大学学报（自然科学版），2004，25（3）：36－38.

［4］DUAN B Q，SI C L.Comprehensive risk assessment model of complex product systems innovation based on fuzzy AHP［J］.Journal of Tongji University，2008，36（7）：1002－1005.

［5］SRDJEVIC B，MEDEIROS Y D P.Fuzzy AHP assessment of water management plans［J］.Water Resources Management，2008，22（7）：877－894.

［6］WANG L，CHU J，WU J.Selection of optimum maintenance strategies based on a fuzzy analytic hierarchy process［J］.International Journal of Production Economics，2007，107（1）：51-163

［7］BESKESE A，BOZBURA F T.Prioritization of organizational capital measurement indicators using fuzzy AHP［J］.International Journal of Approximate Reasoning，2007，44（2）：124－147.

［8］王凯甲，刘铁民.基于模糊层次分析法的网络环境下企业财务风险评价［J］.经济管理者，2009，24：141－143.

［9］孙鑫，徐杨，林柏泉，等.煤与瓦斯突出影响因素评价分析的模糊层次分析方法 ［J］.中国安全科学学报，2009，19（10）：145－149.

［10］隋明刚，魏嶷.Fuzzy AHP中权重确定方法的探讨与改进［J］.山西大学学报（自然科学 版），2000，23（3）：218－220.

Ship Survivability Assessment Using Improved Fuzzy Analytical Hierarchy Process

Liu Jin－xiang Jin Tao
College of Naval Architecture and Power，Naval University of Engineering，Wuhan 430033，China

For the complexity of ship systems，the total ship survivability assessment is required to be dealt with by evaluating separate subsystem or multi－level subsystems respectively，which are to get the complete description through a range of indices of these subsystems.Traditional method using fuzzy analytical hierarchy process（FAHP）in coping with this issue has two shortfalls，on the one hand it likely lead to incorrect calculation，while the other it is unable to calculate the weight of interrelated factors between different hierarchies，which limits the scope of the use of FAHP method.A hierarchy model was built by an improved analytical hierarchy process to determine the weight of interrelated factors，and the weight sequence of subsystems were obtained by calculation.An actual assessment demonstrated that the results could reflect the practical conditions of ship systems.Meanwhile，according to the calculated results，the weak links of the total ship survivability can be found，which provides a theoretical basis and method of decision－making for ship damage control operation.

ship survivability；assessment；fuzzy analytical hierarchy process（FAHP）；decision making of damage control

U674.7

：A

：1673－3185（2011）04－67－05

2010-07-05

刘晋祥（1988－），男，硕士研究生。研究方向：舰艇生命力评估。E-mail：liu_liu456＠126.com

金 涛（1966－），男，教授，博士生导师。研究方向：舰艇生命力评估。

10.3969/j.issn.1673-3185.2011.04.014