用G'/G-展开法求解(2+1)维Ablow itz-Ladik方程

李四伟，张金良

(河南科技大学数学与统计学院，河南洛阳471003)

0 前言

由于非线性微分－差分方程(组)在非线性光学、原子物理、凝聚态物理、生物物理等领域有着广泛的应用，如脉冲在光纤中的传播、等离子体物理中Langmuir波的自聚焦和爆破等，因此，非线性微分－差分方程(组)已引起众多学者广泛的兴趣。对于非线性微分－差分方程(组)，已有很多研究方法如双线性方法［1］、达布变换法［2］、Backlund变换法［3］、广义的微分变换法［4］、离散的Sine－Gordon方程展开法［5］、指数函数展开法［6］、Jacobi椭圆函数展开法［7］、扩展的双曲正切函数展开法［8］、G'/G－展开法［9－11］等。到目前为止，没有一种统一的方法能求解出非线性微分－差分方程(组)的所有精确解。

文献［12］研究了(2+1)维Ablowitz－Ladik(AL－NLS)方程

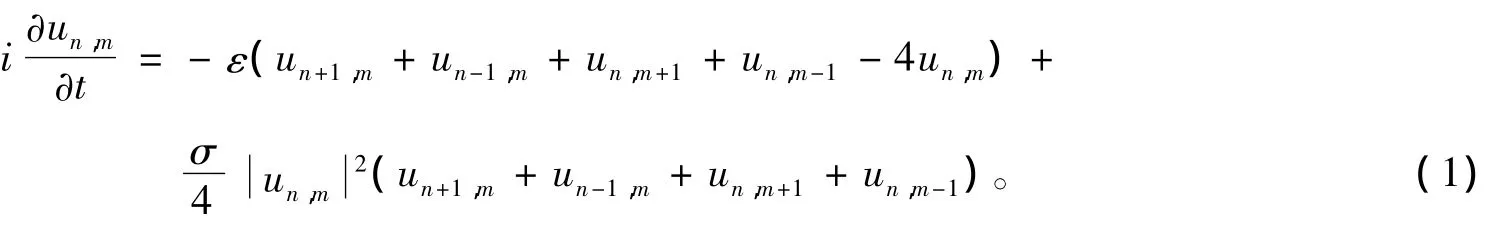
文献［13］证明了方程(1)是不完全可积的，并对其孤波性质进行了系统分析，得到对于任意小的格子空间△x，此方程均有稳定的孤子解;求解出了方程(1)的精确线孤子解(不稳定):

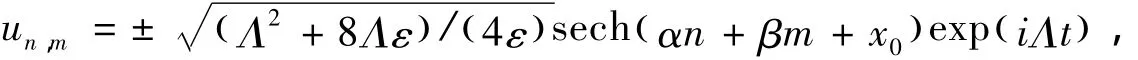
由于方程(1)的精确解具有很重要的理论意义和实用价值，因此，本文利用G'/G－展开法求解方程(1)的精确解，并成功得到它的三种类型的精确行波解。

1 (2+1)维Ablow itz-Ladik方程的精确解

由于un，m(t)为复函数，设

把式(2)代入方程(1)，令实部和虚部等于零，得

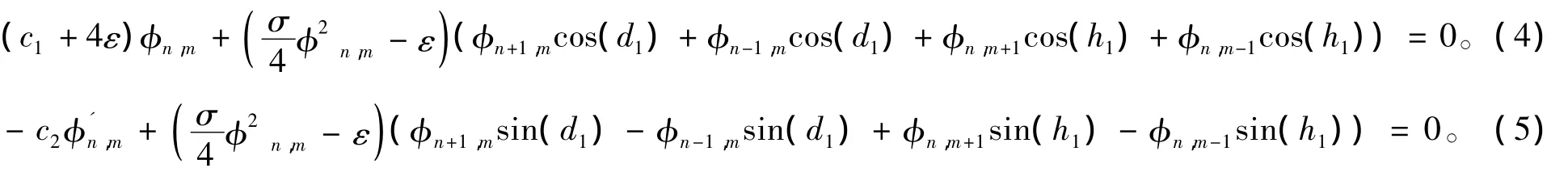
依据齐次平衡原则，令

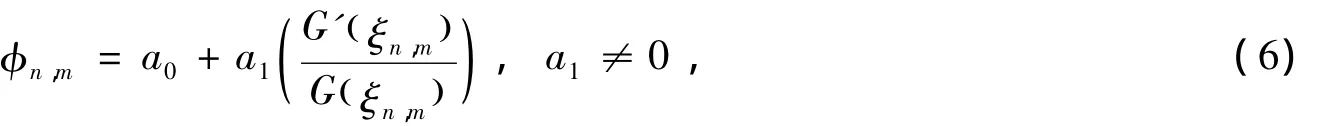
其中，a0、a1为待定常数;G (ξn，m)满足

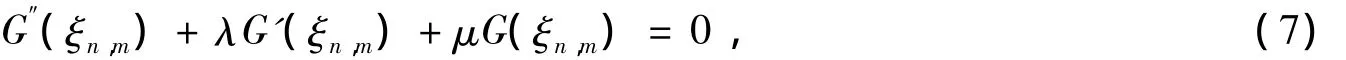
λ、μ为任意常数。

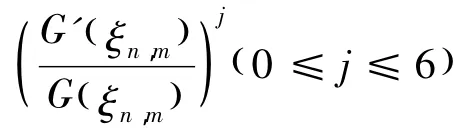
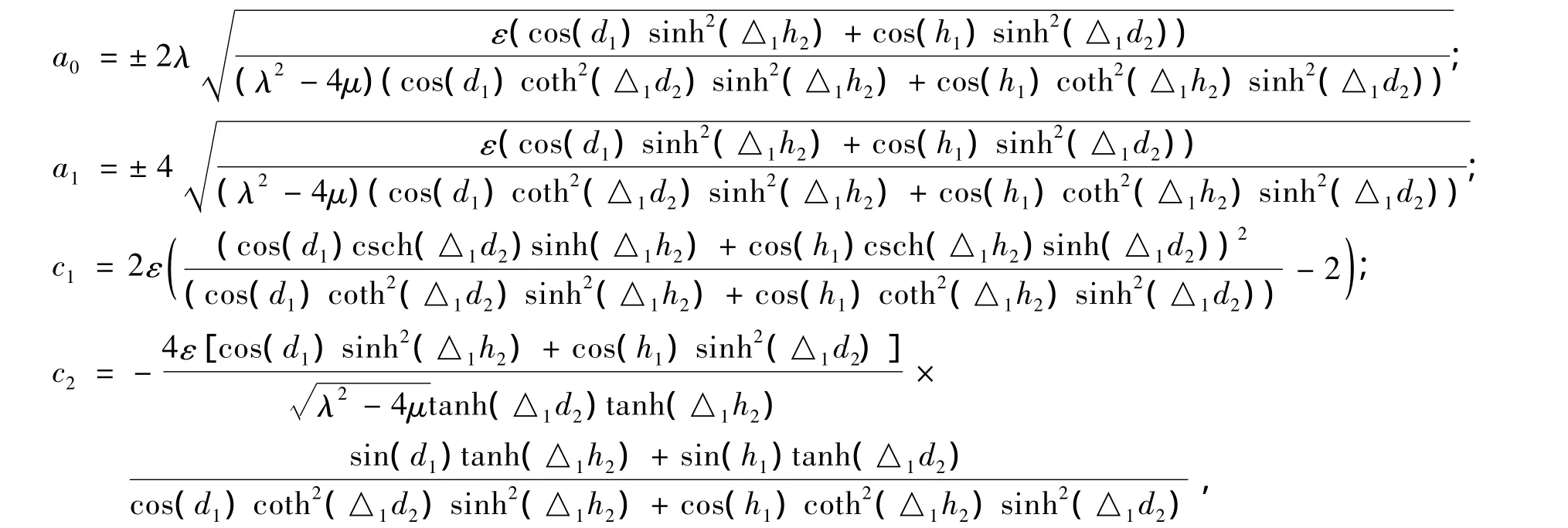
其中，△1=;ζ1、ζ2、d2和h2为任意常数;d1和h1为满足cos(d1)cos(h1)＞0的任意常数;耦合强度ε=1/△x2。

利用方程(7)的解，可导出方程(1)的精确解:

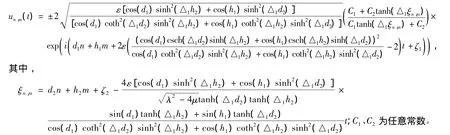
情形2 当λ2－4μ＜0时，类似于情形1，可得出方程(1)的精确解:

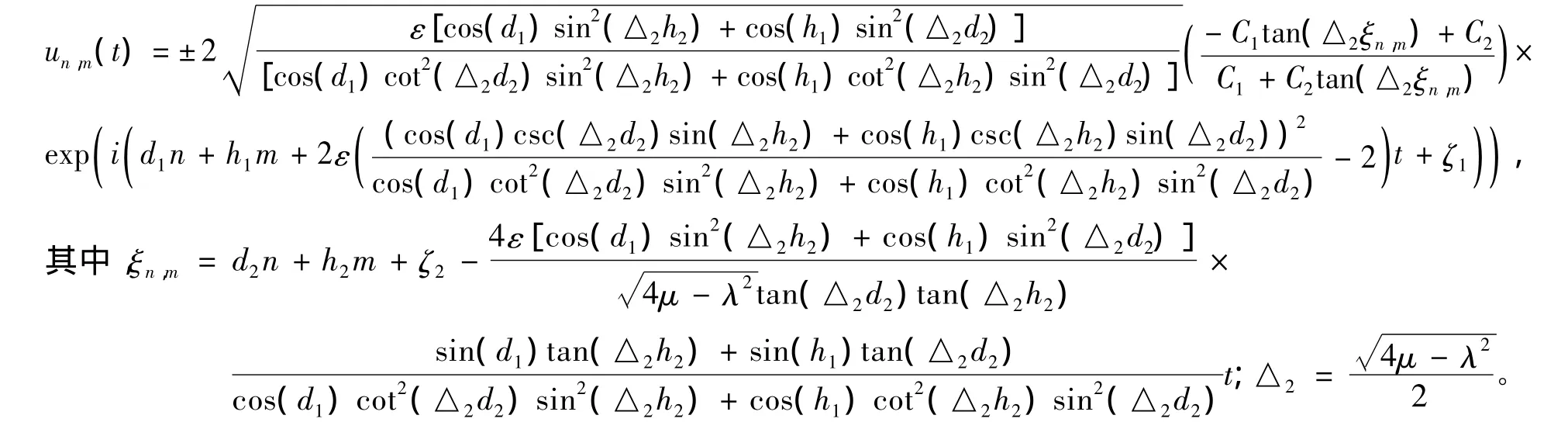
情形3 当λ2－4μ=0时，类似于情形1，可得方程(1)的解为:

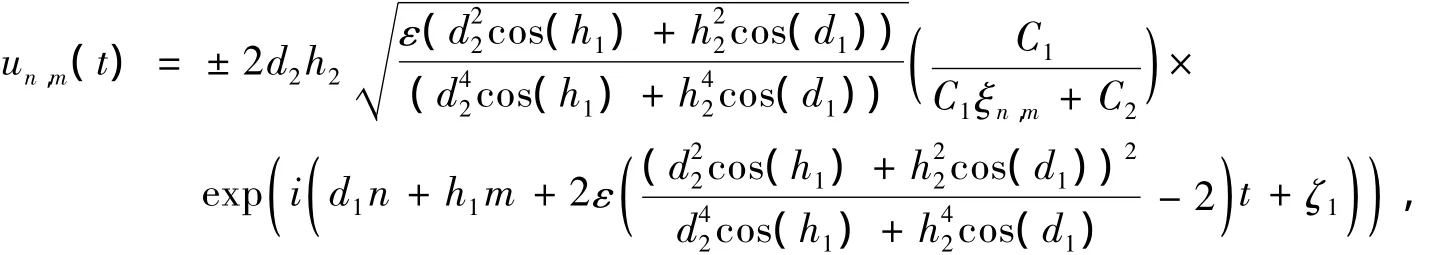
2 结论

本文将G'/G－展开法应用于(2+1)维Ablowitz－Ladik(AL－NLS)方程的求解中，当耦合强度ε= 1/△x2，σ=1(散焦)时，得到了该方程的双曲函数形式的精确解、三角函数形式的周期波解和有理函数形式的行波解，这些精确解含有较多的任意参数。利用Mathematica软件，验证了所得精确解的正确性。可见，在求解非线性微分－差分方程(组)精确解方面，G'/G－展开法是一个非常有效、直接、简便的方法。

［1］ Hu X B，Ma W X.Application of Hirota’s Bilinear Formalism to the Toeplitz Lattice－some Special Soliton－like Solutions［J］.Phys Lett A，2002，293:161－165.

［2］ Nimmo J JC.Darboux Transformations for Discrete Systems［J］.Chaos，Solitons and Fractals，2000，11:115－120.

［3］ Sun M N，Deng SF，Chen D Y.The Backlund Transformation and Novel Solutions for the Toda Lattice［J］.Chaos，Solitons and Fractals，2005，23:1169－1175.

［4］ Zou L，Wang Z，Zong Z.Generalized Differential Transform Method to Differential－difference Equation［J］.Phys Lett A，2009，373:4142－4151.

［5］ Yan Z Y.Discrete Exact Solutions of Modified Volterra and Volterra Lattice Equations via the New Discrete Sine－Gordon Expansion Algorithm［J］.Nonlinear Analysis，2006，64:1798－1811.

［6］ Bekir A.Application of the Exp－function Method for Nonlinear Differential－difference Equations［J］.Applied Mathematics and Computation，2010，215:4049－4053.

［7］ Yong X L，Zeng X，Zhang Z Y，et al.Symbolic Computation of Jacobi Elliptic Function Solutions to Nonlinear Differentialdifference Equations［J］.Computers and Mathematicswith Applications，2009，57:1107－1114.

［8］ Wang Z，Zhang H Q.A Symbolic Computational Method for Constructing Exact Solutions to Differential－difference Equations［J］.Applied Mathematics and Computation，2006，178:431－440.

［9］ Aslan I.Discrete Exact Solutions to Some Nonlinear Differential－difference Equations Via the(G'/G)－expansion Method［J］.Applied Mathematics and Computation，2009，215:3140－3147.

［10］ 牛艳霞，李二强，张金良.利用(G'/G)－展开法求解2+1维破裂孤子方程组［J］.河南科技大学学报:自然科学版，2008，29(5):73－76.

［11］ 李四伟，张金良.用(G'/G)－展开法求解耦合离散非线性Schrönger方程组的精确解［J］.河南科技大学学报:自然科学版，2010，31(5):87－90.

［12］ Ablowitz M J，Prinari B，Trubatch A D.Discrete and Continuous Nonlinear Schrodinger Systems［M］.Cambridge: Cambridge University Press，2004.

［13］ Kevrekidis PG，Herring G J，Lafortune S，et al.The Higher－dimensional Ablowitz－Ladik Model:from(non－)Integrability and Solitary Waves to Surprising Collapse Properties and More Exotic Solutions［Z］.arXiv:0907.1386vl，2009:1－4.