可靠性分析在边坡稳定性中的应用

倪侃

（中国葛州坝新疆工程局，湖北宜昌 443200）

0 引言

随着我国工程建设的迅速发展，越来越多的公路、铁路、水利等工程建设中都存在边坡稳定性问题。而边坡稳定性评价结果的正确与否直接关系到边坡工程的成败。[1]目前，在工程中常用传统的极限平衡理论来计算边坡的安全系数，以及随着计算机的普及，发展起来的各种数值算法，和数值算法与极限平衡理论的结合，这些方法虽然操作简单，而且结果明确，但由于边坡稳定受多方面因素影响，而各因素具有不确定性（模糊性、随机性、信息不完全性和未确定性）和复杂性，故传统的确定性分析方法用于边坡分析，结果不十分理想。[1]

可靠度理论建立在概率统计的基础上，以随机变量和随机过程为研究对象，它与定值分析法最大的区别是考虑了变量的随机性，并用严格的概率来度量结构的安全度，因此，它更符合客观实际。[2]

1 理论基础

1.1 蒙特卡洛法

为纪念著名的赌城——Monte Carlo，人们将反演过程中任何一个阶段，用随机（或伪随机）发生器产生模型，以实现模型全空间搜索的方法统称为蒙特卡洛反演法。

对蒙特卡洛法之所以有兴趣，是因为它可以解决其它反演方法难以解决的许多问题。诸如，多参数反演、多个极值的高次非线性反演等。

假如，已知待求模型的参数的上下界限，

minfα≤mα≤msupα(α∈IM)

式中：minfα代表第α个模型参数的下界；msupα代表第α个模型参数的上界。

这里有两种方法对模型空间进行搜索，一种是彻底地搜索法，把模型空间允许的范围都搜索到，看哪一个模型，或哪一组模型的计算值（d(m)）和观测数据（d）拟合最好。这种方法也叫穷举法；另一种搜索是在模型空间允许的范围内随机地搜索，对每一个随机产生的模型计算其理论值并把它与观测值进行比较，看其是否可以接受，这就是传统的蒙特卡洛法。

1.2 简化的Bishop方法

简化的Bishop方法是国际公认的一种比较精确的计算方法[4]。在我国的岩土工程界得到了广泛的应用，并纳入了我国的建筑规范。

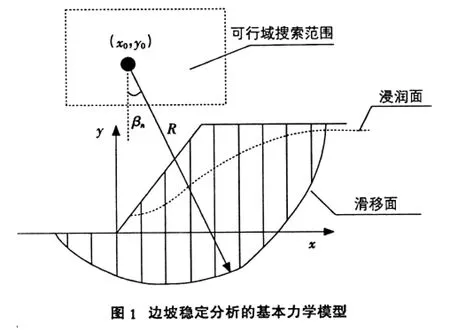
简化的Bishop法的基本假设如下：滑裂面的形状为圆弧形，土条间只有水平推力，条间剪力为零。如图1，2所示，只考虑条块间的水平作用力且不计力矩平衡，当假定了滑动面的坐标曲线以后，边坡的安全系数为5：

f=∑[(Wntanφn+cnbn-unbn)/(cosβn+sinβntanφn/f)]/∑(Wnsinβn)

式中：f为边坡稳定安全系数；Wn为第n块滑体自重；φn为第n块滑体沿滑动面土的内摩擦角；cn为第n块滑体沿滑动面土的粘聚力；bn为第n块滑体沿滑动面的长度；βn为第n块土条底边倾角；un为作用于土条底边上的孔隙水压力。

2 软件介绍

本论文采用的是加拿大Rocscience公司生产的系列岩土软件之一的SLIDE5.014版本作为计算工具。

SLIDE是一个可以用于岩质或土质边坡弧形或非弧形破坏面的稳定性评价软件。SLIDE是一个操作简单，但是可以很容易建立复杂模型，并快速分析得到结果的程序。在SLIDE中可以进行外部加载、地下水和支护系统模拟。

SLIDE还有扩展地进行可靠性分析功能，在一个可靠性边坡稳定分析中，使用者需要首先对输入参数（如材料属性、支护属性、荷载属性、潜水面的定位等）设置统计分布。

SLIDE软件中内置包括简化的Bishop方法、M orgenstern-Price方法和Janbu方法在内的多达9种确定性计算方法，本文采用的是其中简化的Bishop方法。

3 算例

建立一个简单均质材料边坡，如图3所示。

本算例假定粘聚力、摩擦角、岩体密度和潜水面为随机变量。随机变量的采样方法为Monte Carlo法，采样率为10 000。

首先采用图3所示的潜水面为平均潜水面，采用完全边坡饱水状态为最大潜水面来计算边坡潜水面的随机分布。粘聚力、摩擦角和岩体密度采用的统计参数如表1所示。

表1 随机变量的统计参数

因为实际上，Mohr-Coulomb材料的粘聚力和摩擦角是相关的，也就是低的粘聚力会有高的摩擦角，反之亦然。因此，在随机取样之前，还需要首先定义粘聚力和摩擦角的相关系数，以便他们与实际变化相符，这里选择其相关系数为-0.5。

经过软件计算，得到可靠性分析结果，其中确定性安全系数FS(determ inistic)为不考虑参数的随机性情况下计算得到的边坡安全系数；而平均安全系数FS(mean)为由随机参数计算得到边坡安全系数的平均值，由于参数选择的有限性，平均安全系数值和确定性安全系数值略有差异；失效概率(PF)为考虑参数随机性计算得到小于1的安全系数个数占总采样率的百分比。

由最终的可靠性计算结果可以看出，虽然不考虑参数的随机性计算得到的确定性安全系数(FS(determ inistic))要大于1，表示此边坡处于安全状态，但是一旦考虑参数的随机性，却得到边坡的失效概率(PF)达到36.10%之高，表示此边坡需要进行部分支护处理了，而不应该把它看成一个完全安全稳定的边坡。

可见，通过确定性方法计算得到的边坡稳定性有时是不可靠的，应该尽量采用考虑参数随机性的可靠性分析方法来完整的评价一个边坡的稳定性。

［1］夏元友，李梅.边坡稳定性评价方法研究及发展趋势［J］.岩石力学与工程学报，2002，21（7）：1087-1091.

［2］谭晓慧.多滑面边坡的可靠性分析［J］.岩石力学与工程学报，2001，20（6）：822-825.

［3］王家映.蒙特卡洛法［J］.工程地球物理学报.2007，4（2）：81-85.

［4］朱大勇，基于余推力法的边坡临界滑移场［J］，岩石力学与工程学报，1999，18（6）：607-670.

［5］江见鲸.土建工程使用计算程序选编［M］.北京：地震出版社，1992.