非线性系统神经网络输出稳定控制器的设计
2011-03-27欧阳林群王效华
欧阳林群, 王效华
(武夷学院电子工程系,福建武夷山 354300)
0 引 言
实际的非线性系统中存在时变性、不确定性等因素,使得传统控制方法[1-3]难以实行有效的稳定性控制。系统运行过程的复杂性使得控制系统的控制面临两大主要难题:一个是难以用传统的理论和方法对系统实时在线建模;另一个是难以用基于解析模型的解耦理论对其实施控制。已有很多学者[4-7]对非线性的控制作了研究。但是这些理论都基于一个前提:这就是必须写出被控系统精确模型,而这一点在现实中几乎不可能做到,尤其是对过程控制中系统随着运行工况的不时改变、系统结构和参数不确定、非线性、滞后、诸多干扰等因素更是无法写出其数学模型。
神经网络具有良好的非线性逼近能力,可以克服控制器对被控系统精确数学模型的依赖,因此,在非线性系统的控制中得到了广泛的应用。
在借鉴吸收前人研究的基础上,文中将神经网络引入到非线性系统的控制中,利用神经网络具有逼近外界干扰信号[8-12]的能力,抵消系统所受扰动的影响,采用李雅普诺夫函数法给出了稳定性证明,并用仿真实验验证。
1 神经网络算法分析
根据非线性系统稳定输出设计的自适应反馈控制的要求,首先对所用神经网络做数学分析。实际系统在运行过程中,不仅会受到系统内部的参数不确定性的影响,还会受到外部扰动的影响。神经网络通过足够的输入信息和隐含层神经元数目,可以任意精度逼近连续非线性函数。因此,通过引入该网络来补偿系统所受到的外部干扰,实现基于神经网络的输出跟踪控制,提高系统的鲁棒性能。
1.1 神经网络的逼近性
神经网络的基本控制特性就是其任意精度的逼近性[13],设定 f(x)是映射Rn→Rm上的函数,那么在紧致集S∈Rn上的任一点x,隐层神经元权重和阈值的关系式:

式中:x——输入向量;
φ(◦)——激活函数;
W——神经网络输出层的输入矩阵;
ε(x)——近似误差。
方程(1)表明,在任一紧致集合中,神经网络能估测连续函数的状态。实际上对一个正数εN,存在神经网络参数满足ε(x)≤εN(x∈S)。对于神经网络,φ(x)满足φ(x)=σ(VTx),其中V是首层的权值矩阵,σ(x)是S型函数。如果V是固定的,则神经网络中唯一的设计参数就是W,则系统就变得更容易训练。神经元隐层的数目越多,估测误差ε(x)越小。对单层神经网络函数,逼近误差ε(x)是有界的。
1.2 非线性系统
为了分析和设计非线性控制器,设定多输入单输出(MISO)非线性系统用下面的式子描述:
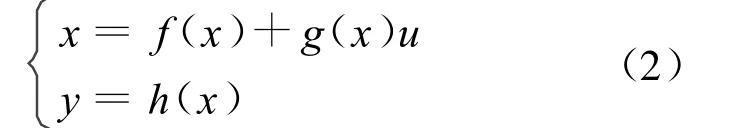
式中:x——状态向量;
u——输入向量;
y——输出向量。
2 神经网络控制方案的设计
2.1 布鲁诺标准型
精确线性化定理指出:设式(2)中h(x)存在m维函数,使得系统有相对阶向量[r1,r2,…,rm],且系统总相对阶r=r1+r2+…+rm=n(n为系统维数),即系统相对阶等于系统维数,那么该系统就能实现精确线性化[14]。
设一个五阶非线性系统,即式(2)中n=5。设输出误差为:
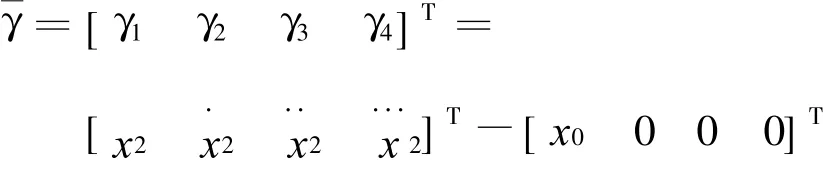
则跟踪误差的布鲁诺标准型为:

式中:u——系统的控制量;
d——有界干扰;
控制目标:如果系统满足输出反馈线性化的条件,运用文中提出的控制器,输出量能稳定在一个平衡范围之内。
2.2 相关假设
假设1:非线性系统(2)是输入一状态有界稳定的。
假设2:非线性系统(2)所有状态可测。
2.3 神经网络控制器的设计
定义滤波误差σ如下:

其中,∧=[λ1 λ2 λ3]T是系数变量,满足当σ→0时,γ→0,其中s3+λ3s2+λ2s+λ1是Hurwitz多项式。
对上式求微分,并且把式(3)代入,则
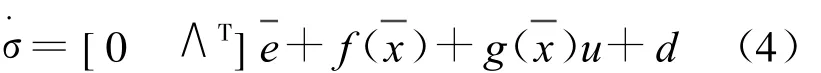
根据反馈线性化理论,期望的希望输入信号可以表达为:

式中:Kv——常系数。

考虑到误差信号,则上式变为:

把式(7)代入式(4)并整理,可以得到
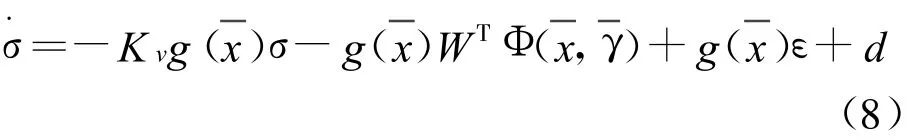
其中:

定义设定的控制信号:
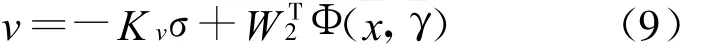
如果umax为最大信号值,则系统的控制信号可以表示为:
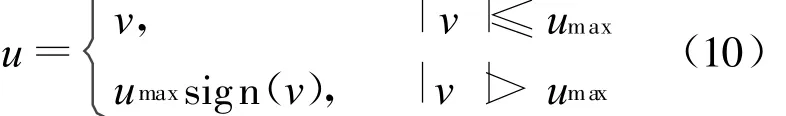
2.4 含NN的控制系统框图
含神经网络的非线性控制系统框图如图1所示。

图1 含神经网络的非线性控制系统框图
为了有效实现控制目的,控制图采用双环反馈,保证被控制非线性系统的稳定运行。内环为非线性NN的非线性控制,用来估测系统的动态运行,外环为PID跟踪控制。
非线性系统结构框图工作原理如下:
设d为系统未知干扰,权值误差是ε,均是有界的。对于权值W满足下式:
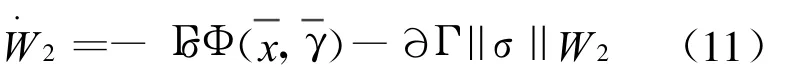
2.5 李雅普诺夫方法证明稳定性
李雅普诺夫函数方法的特点是不用求解系统的动态方程或分析参数特征根的实数部分正负特性,直接用确定并分析所研究状态点处的广义能量函数来判别系统的稳定性。将李雅普诺夫函数方法应用于神经网络的稳定分析,可用来推导条件来保证权值的收敛。
运用选取V为李雅普诺夫函数,且V∈R,

计算导数得


化简后得到:
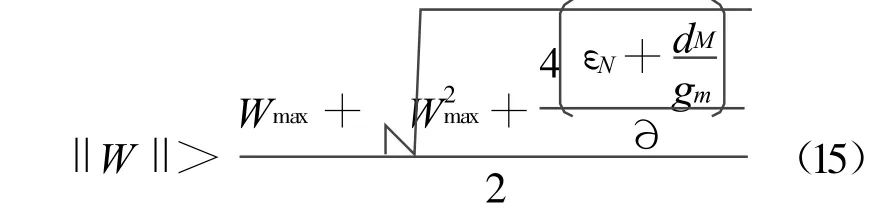
从上面分析可知,对于非线性系统的稳定,在用神经网络优化系统时,神经网络隐层的权值在(0,1)之间选择,则需要满足式(15)。
3 仿真与分析
3.1 仿真
为了验证设计的基于李雅普诺夫的非线性神经网络控制方法的控制效果,采用一个单机电力系统模型[15]作为仿真案例。神经网络输入层的权值取(0,1)之间的一个常数。
取参数分别为:

通过仿真,得到系统变化曲线如图2所示。
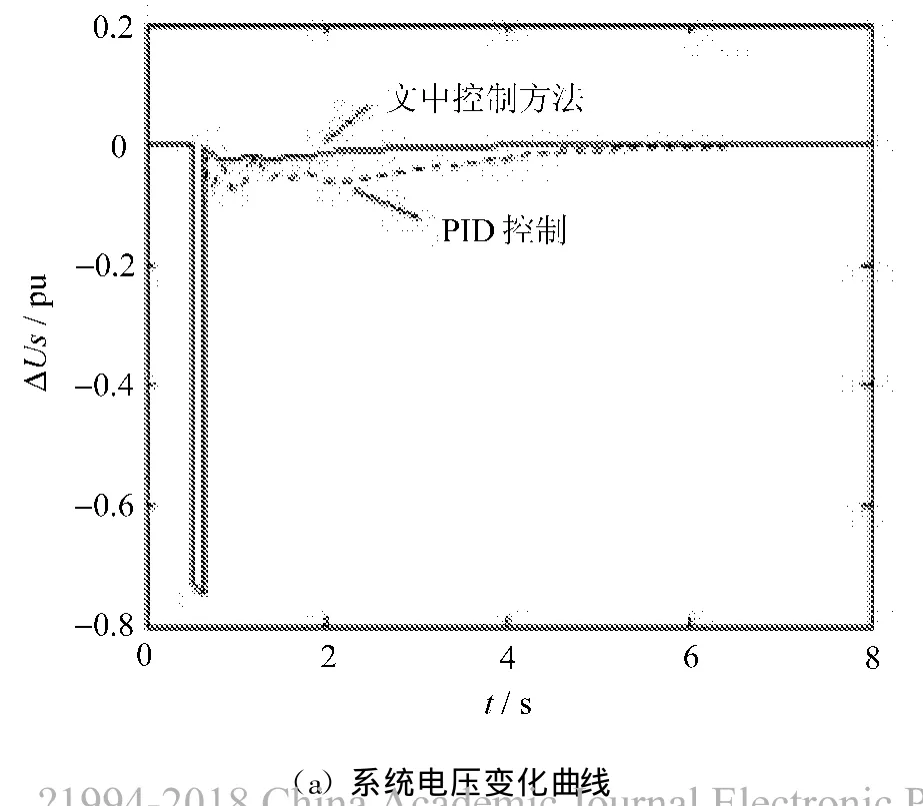

图2 系统变化曲线图
3.2 结果分析
从仿真结果可以看出,文中提出的非线性控制器能够很好地避免系统由于外界故障造成的不平衡,在经过振荡后神经网络非线性系统可以调节系统的运行状态。
4 结 语
设计含有神经网络的非线性系统的反馈稳定控制器,神经网络算法具有朝最小误差方向调整权值的内在因素,用李雅普诺夫函数方法对神经网络算法收敛做分析,将设计的控制器运用于单机无穷大电力系统。仿真结果表明,提出的非线性控制器可以保证系统在受到外界扰动,平衡状态被打破时对系统做有效的补偿。
[1] 曹建福,韩崇昭,方洋旺.非线性系统理论及应用[M].西安:西安交通大学出版社,2001.
[2] 廖晓听.稳定性的数学理论及应用[M].2版.武汉:华中师范大学出版社,2001.
[3] 李基成.同步发电机励磁系统设计[M].北京:中国电力出版社,2002:8-20.
[4] 朱方,赵红光,刘增煌,等.大区电网互联对电力系统动态稳定性的影响[J].中国电机工程学报,2007,27(1):1-7.
[5] 陈利芳,陈天禄.浅谈自并励励磁系统在大容量机组中的应用[J].继电器,2007,35(1):81-84.
[6] 杨海龙,张天宇,郭骥俊.励磁调节器中PSS对系统稳定性的作用及参数设置[J].华北电力技术,2005(12):12-14.
[7] 刘恩东,井元伟,王珂,等.基于神经网络的非线性汽门控制器鲁棒逆推设计[J].电力自动化设备,2005,25(10):13-16.
[8] 康锦萍,张粒子,徐英辉,等.基于神经网络的快速汽门暂态稳定控制器的研究[J].电网技术,2003,27(11):22-25.
[9] HAN Yingduo,XIU Lincheng,WANG Zhonghong,et al.Artificial neural networks controlled fast valving in a power generation plant[J].IEEE Trans.Neural Networks,1997,8(2):373-389.
[10] Venayagamoorthy G K,Harly R G,Wunsch D C. Implementation of adaptive critic-based neurocontrollers for turbogenerators in a multimachine power system[J].IEEE Trans.Neural Networks,2003,14(5):1047-1064.
[11] 张腾,戴先中.汽门开度的神经网络广义逆系统控制[J].电力系统自动化,2000,24(17):25-27.
[12] 戴先中,张腾,张凯锋,等.发电机励磁与汽门系统解耦控制的神经网络逆系统方法[J].中国电机工程学报,2002,22(11):75-80.
[13] Liu Lili.Guaranteed cost control of singular networked control systems with time-delay[C]// 2008CCDC.Yantai:Institute of Electrical and E-lectronics Engineers Computer Society,2008:415-418.
[14] 胡跃明.非线性控制系统理论与应用[M].北京:国防工业出版社,2002:110-121.
[15] KUNDER P.Power system stability and control [M].New York:McGraw-Hill Inc,1994.
