大型真空消毒柜屈曲分析

2011-03-26苏文献刘晓东

上海理工大学学报 2011年2期

苏文献, 刘晓东

(上海理工大学能源与动力工程学院,上海 200093)

压力容器的屈曲或失稳是指承受外压载荷的壳体当外压载荷增大到某一数值时,壳体会突然失去原来的形状,被压扁或出现壳体不能恢复原状的现象[1].外压载荷作用下,壳体往往在应力满足强度要求的情况下也会屈曲,因此,需要确定外压容器的临界载荷和其失稳状态,保证其不会发生破坏性的变形并改进其形体结构,提高容器抗失稳能力[2].但对于某些受外压的压力容器,由于其结构的特殊性,在受到超过临界载荷的外载荷作用下会产生后屈曲行为.容器受后屈曲的影响使容器失稳但并不会马上被压垮,还能继续承受更大的载荷.本文所讨论的真空消毒柜就是一个受后屈曲影响的容器.

1 模型的建立

1.1 问题的描述

某工程中的真空消毒柜为箱体结构,在表面上焊有截面为矩形的夹套.当消毒柜工作时,夹套通过热流使该真空设备升温,从而达到消毒目的.但夹套同时也起到加强筋的作用,大大提高了设备的强度和抗屈曲能力.

该真空消毒柜箱体的尺寸为 6 560×2 850× 2 700 mm3,壁厚为5 mm.夹套的矩形截面尺寸为200×150×8 mm3,顶部开有一圆形接管φ 192×8 mm2,左右两边各有一个方形接管182×168 mm2.由于门为独立的结构,对门的分析另外考虑,在此不对门进行分析,但是,门对箱体的作用力已考虑在内,即在箱体上施加门的等效端面力.其简图如图1所示,基本参数如表1所示.

图1 消毒柜简图Fig.1 Diagram of sterilization tank

表1 设计参数表Tab.1 Design parameters

1.2 有限元模型的建立

对带夹套的消毒柜所建立的几何模型如图 2所示.

图2 消毒柜模型图Fig.2 Solid model of sterilization tank

采用大型有限元分析软件ANSYS11.0进行分析.由于消毒柜、夹套和接管都属于板壳结构,因此,有限元网格划分采用壳单元shell181,得到有限元模型节点总数为28 813,如图3所示.消毒柜的受力状况如图4所示.

图3 消毒柜网格图Fig.3 Mesh of sterilization tank

图4 消毒柜载荷图Fig.4 Load model of sterilization tank

1.3 边界条件及静力强度分析

根据消毒柜的实际边界条件对模型进行约束.在底部边上夹套一边加全约束,在箱体另一边的夹套边上仅约束y,z方向.其中,x为轴向方向,y为高度方向,z为宽度方向.材料属性为各向同性,材料参数如表2所示.

表2 材料参数Tab.2 Material parameters

通过静力分析得到箱体的应力分布图,如图5和图6所示,其顶层和中间层的最大应力值分别为170.328,154.223 MPa.对于强度问题,文献[3]规定一次局部薄膜应力的值不得超过许用载荷的1.5倍,一次局部薄膜应力加二次应力的值不得超过许用载荷的3倍.由于本模型运用壳单元,结果显示顶层和中间层的最大值分别小于规定的值,则静力强度满足要求.

图5 顶层应力分布图Fig.5 Linearized stress of top layer

图6 中间层应力分布图Fig.6 Linearized stress of middle layer

2 屈曲分析

2.1 理论解析法求临界载荷

由于本模型为非回转壳体,因此,使用能量分析法对其进行计算[4].能量分析法指从能量守恒原理出发,当壳体受外载荷而屈曲时,存储于壳体内的形变势能U应恒等于外力做的功W,即U=W.由此可求出壳体的临界载荷.该方法适用于不规则形状、非均匀荷载变截面以及各向异性材料等问题的求解.其临界失稳压力为[5]

式中,Pcr为弹性失稳时的临界压力,MPa;E为设计温度下材料的弹性模量,MPa;δe为为壳体的有效厚度,mm;R为壳体球面当量半径,mm;参数a=[5 (23-9μ)/(7-μ)(1-μ2)]1/4.

对于本例,泊松比μ=0.3,故化简公式为

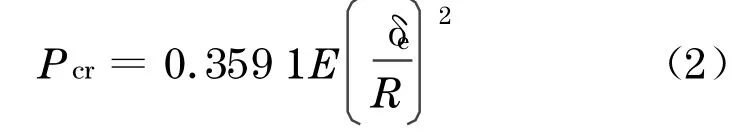
将表2中数据代入式(1)中,得到计算临界载荷为0.966 91 MPa.

能量法计算得到的结果与实验结果有所偏差,但偏差程度较小.

2.2 有限元线性屈曲分析

线性屈曲分析又称特征值屈曲分析,其以完善结构为研究对象,以小位移线性假定理论为基础,来预测临界失稳力[6].一般被认为是在材料弹性范围内的屈曲分析,与实际结果偏差较大.线性屈曲分析为非线性屈曲分析可能发生的屈曲模态及临界载荷范围可提供参考.

特征值表示给定载荷的比例因子.当在模型上施加的是单位载荷时,计算结果得到的特征值就是临界载荷;当在模型上施加的是实际载荷时,屈曲载荷等于实际载荷与对应的特征值的乘积.对于本模型施加的是单位载荷,得到的屈曲临界载荷为1.403 MPa,并得到屈曲模态,如图7所示.

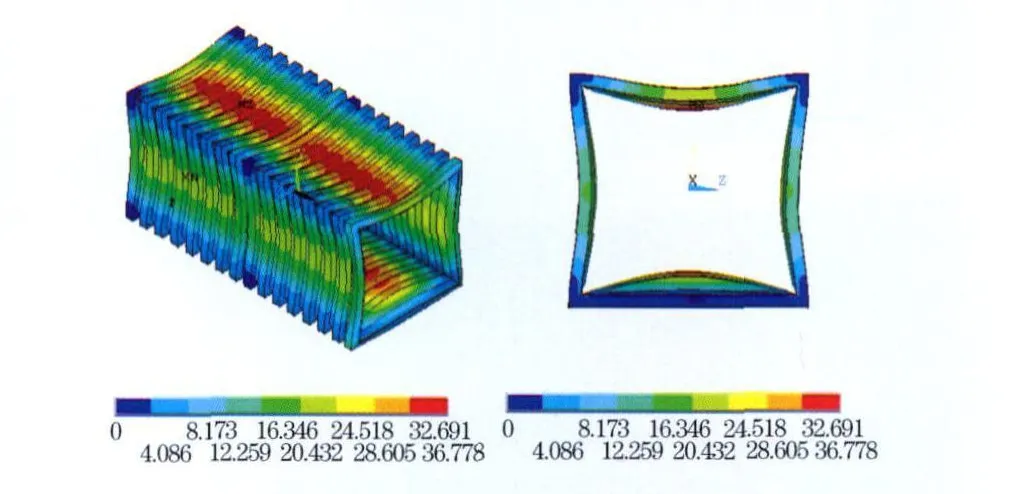
图7 线性屈曲模态图Fig.7 Mode of linear buckling of sterilization tank

2.3 有限元非线性屈曲分析

非线性屈曲分析是用一种逐渐增加载荷的非线性静力分析技术来求得结构开始变得不稳定时的临界荷载.通常在容器上施加微小扰动使其发生屈曲.本文对容器模型进行非线性屈曲分析,依据文献[1],考虑到容器的大变形效应,因此,材料特性设置为几何非线性,即在特征值屈曲分析的屈曲模态取其变形的0.1%作为非线性分析的屈曲扰动.依据文献[7]在对压力容器进行屈曲分析时求得的特征值屈曲临界载荷的基础上扩大1.1～1.2倍作为非线性分析的加载载荷,保证能够在非线性分析中容器发生失稳,从而得到临界载荷.因此,本文取线性屈曲分析得到的临界载荷的1.2倍作为非线性屈曲分析的施加载荷.运用增量法逐渐加载,即设置多个载荷步来逐渐增加载荷,使其变得不稳定起来.当其中某个载荷对应的解不收敛时,说明此时的载荷达到或超过临界载荷,容器失稳,在位移载荷图上表现为曲线的突变.非线性模态如图8所示.由图8中得到最大值出现在上表面(y方向)夹套之间,并做出最大值在y方向上位移-载荷关系曲线,如图9所示.s为位移,P为载荷.

图8 非线性屈曲模态图Fig.8 Mode of nonlinear buckling of sterilization tank

图9 非线性位移载荷曲线图Fig.9 Load-displacement of nonlinear buckling

图9中箱体的位移载荷曲线表明,结构从初始的平衡位形突变到与其临近的另一平衡位形,表现出平衡位形的分叉现象,即分叉屈曲.该容器不能被认为是传统意义上的回转壳结构,而应该被看作平板构件的组合.

文献[8]推导出受面内压缩载荷和横向压力的平板计算公式.设有一块材料属性为各向同性的矩形板,长为a,宽为b,厚度为t,分别受到x方向的压缩载荷Px,y方向的压缩载荷Py,以及横向均布压力q,即受到横向压力和面内压缩的共同作用,如图10所示.

导得以量纲一挠度为摄动参数的后屈曲平衡路径[8].

其中

式中,Wnm为该屈曲模态下的板或壳板法向挠度;β为板长宽比;λx,λy为x、y向压应力;α为面内压应力比例值;ε为摄动小参数;m,n为屈曲模态.

图10 矩形板受面内压缩与压力共同作用图Fig.10 Rectangular plate subjected to biaxial compression combined with lateral pressure

根据式(3)和Yamamoto平板屈曲实验结果[8]的位移-载荷曲线如图11所示,并与ANSYS软件做出的非线性屈曲图进行比较.

通过图10和图11的位移-载荷曲线的比较,可以发现3条曲线吻合得较好,说明了本文中所分析的容器属于平板构件,屈曲曲线为分叉点失稳.

依据Koiter理论,当初始后屈曲平衡路径的斜率为正时,则平板构件具有后屈曲强度.板构件后屈曲强度指板与板通过冷弯、焊接及热轨等连接,形成板之间相互约束,板件在受载荷屈曲后,受到其他板件的约束(两板交接处刚度大),板件具有薄膜效应(纵向屈曲变形受到横向薄膜效应的约束),使得板构件整体稳定,并不会被压溃,即板件局部屈曲后并没使整个构件失去稳定,而且还有继续承受更大荷载的能力.因而在本文中ANSYS非线性屈曲分析结果图中发生了失稳却并没有导致整体结构压溃.

图11 理论公式和Yamamoto平板屈曲实验的位移-载荷曲线Fig.11 Load-displacement of nonlinear buckling of the formula and Yamamoto

本文对容器进行非线性分析的临界载荷有两个,即分叉载荷和失稳载荷,前者对应于分叉点,后者对应于结构丧失了继续承载的能力,即压溃.但本文所讨论的容器应从实际使用的安全性方面和做压力容器屈曲分析中线性分析得到的结果一般大于非线性屈曲分析得到的结果的经验方面考虑,并以能量法得到的结果作为参考,故取分叉载荷作为临界载荷,即为1.338 MPa,当取安全系数为3时,得到临界载荷为0.446 MPa,大于其设计压力0.330 MPa.故该设备是安全可靠的.