基于主成分分析法的改进型保障性评价方法
2011-03-24徐廷学程智慧樊庆和
徐廷学,赵 涛,程智慧,樊庆和
(1.海军航空工程学院 a.兵器科学与技术系;b.飞行器工程系,山东 烟台 264001;2.91557部队,浙江 舟山 316000;3.海军装备技术研究所,北京 100072)
保障性是描述武器系统可保障和受保障程度的一种设计特性,它是继可靠性、维修性之后,在20世纪80年代以来才被人们普遍认识、研究与定义的。GJB 451A给出的保障性定义是:“装备的设计特性和计划的保障资源满足平时战备完好性和战时利用率要求的能力”[1]。
保障性评价是将保障性试验与分析所取得的数据资料(包括部署后在使用环境中收集的数据)进行逻辑的集合与综合分析,用以对武器系统的保障性设计和综合保障要素做出决策的一个过程。它是利用保障性的信息,即可靠性、维修性等保障性设计特性和保障系统的保障能力的综合检验信息做出决策的[2]。目前,保障性评价大多采用层次分析法、模糊综合评价法等,并取得了一定的成果,但是这些方法在确定评价指标的权重时受人的主观因素影响较大,而主成分分析法在指标权重的选择上较好地克服了主观因素的影响,较客观地反映样本间的现实关系[3]。
1 主成分分析法的基本理论
1.1 主成分分析法的基本思想
主成分分析法是通过对原来相关的各原始指标作数学变换,在多个指标中寻找相互独立的主成分,这些主成分就是原有指标变量的线性组合,它们充分反映了原来的信息[4]。然后对这些主成分进行综合评价,这就消除了由于指标间相关而在评价时反映的重复信息。指标权重的确定采用信息权重,即通过评价指标所包含的被评价对象分辨信息量来确定的一种权数,客观性强。通过主成分分析,所取主成分个数是小于实际评价指标个数的,这样不但方便了综合评价,也简化了计算。
1.2 主成分分析法的算法步骤
1)原始指标数据的标准化。
设有n个样本,p 项指标,可得数据矩阵X为

式中:n为样本个数;p为指标个数。
在实际应用中,为了消除不同指标间量纲和数量级的不同带来的影响,通常对各个变量作标准化变换[5-6]。在此用Z-score法对数据进行标准化变换,公式如下:

式(1)中:

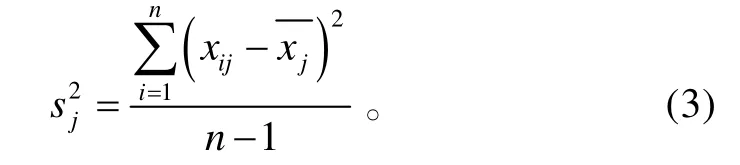
式(2)、(3)中:i=1,2,…,n;j=1,2,…,p。经过变换后的数据均值为0,方差为1。
2)求指标数据的相关矩阵。
定义指标数据的相关矩阵 R=(rjk)p×p为

式中:j=1,2,…,p;k=1,2,…,p;rjk为指标j与指标k的相关系数,

从而有:rii=1,rkj=rjk。
3)求相关矩阵R的特征根λk(k=1,2,…,p)和相应的特征向量。
将标准化的指标变量转换为主成分

式中:g=1,2,…,p;F1称为第一主成分;F2为第二主成分;pF为第p个主成分。
4)求方差贡献率,确定主成分个数。
一般主成分个数等于原始指标个数。如果原始指标个数较多,进行综合评价时就比较麻烦。主成分分析法就是选取少量的m个主成分(m<p)来进行综合评价,同时还要使损失的信息尽可能少。选择m个主成分,实际中通常m的取值使得累计贡献率达到85%以上,即
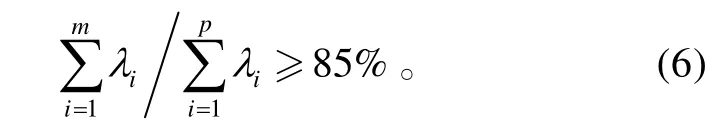
5)对m个主成分进行综合评价。
先取每一个主成分的线性加权值
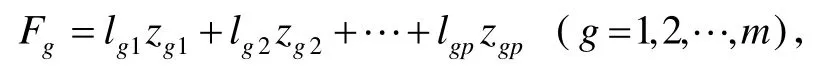
再对m个主成分进行加权求和,即得最终评价值:
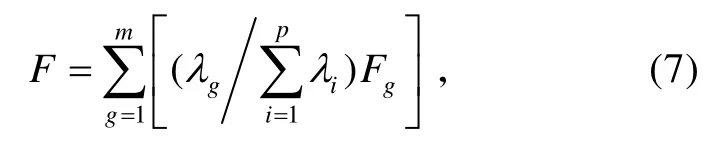
2 指标体系的建立
以某武器系统为例,根据客观性、系统性、完备性、非相容性和科学性的原则[7],并反复向有关专家咨询后,建立其保障性评价指标体系见图1。
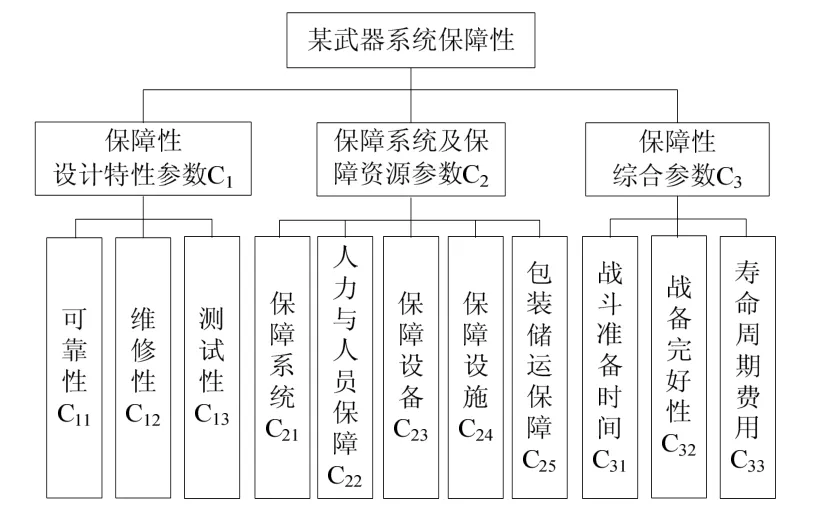
图1 保障性评价指标体系
3 实例验证
下面采用主成分分析法对某武器系统的4种保障性方案进行计算并排序。传统主成分综合评价的权重源于原始数据,强调其权重的客观性。主成分权重的确定更依赖于原始数据的量,而非数据的质,它不会像层次分析法那样,对给定原始数据中具有重要性质的指标变量赋予较大的权重。为了克服这一不足,可将两种方法结合起来,在建立原始矩阵时,利用层次分析法,根据原始指标的重要程度分别赋予相应的权重,并形成新的变量矩阵,接着在这新的变量矩阵的基础上进行主成分分析。这样,在源头上就保证了指标数据的合理性,因主成分分析的权重是建立在原始变量的重要程度得到相应重视的基础上,所以评价结果是客观与主观的综合反映,比传统的主成分分析法更有实际的应用价值。
通过调研,采用专家打分的形式得到表1所示的原始数据。其中:0~59分表示差,60~79分表示一般,80~89分表示良好,90~100分表示优秀,括号中的数值表示指标的权重,是通过层次分析法建立两两比较矩阵并计算得到的[8]。
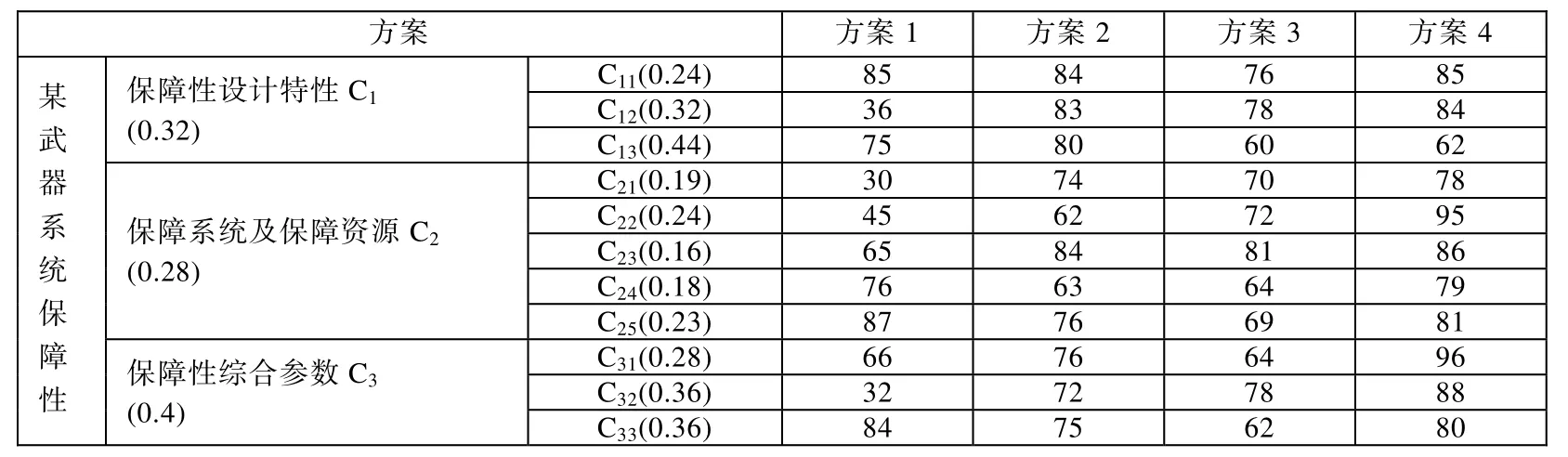
表1 某武器系统保障性方案原始数据
1)将表中的原始数据乘以相应的主观权重,得到原始指标矩阵为
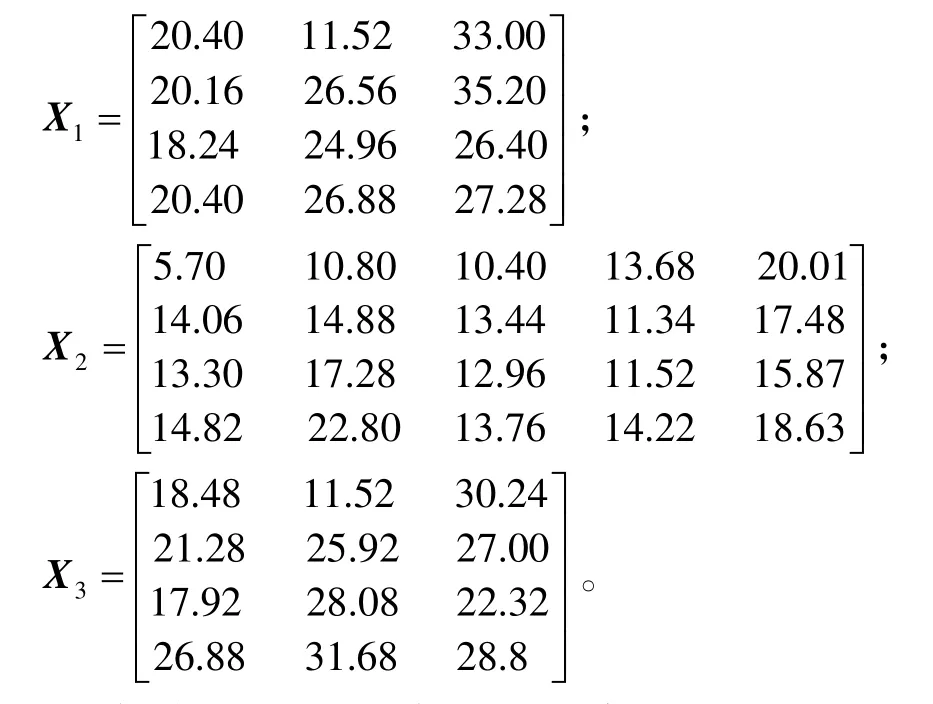
2)根据式(1)~(3)得到标准化矩阵为

3)根据式(4)计算相关矩阵R。


4)求相关矩阵的特征值和特征向量。
用Matlab6.0 软件求得R1的特征根为[9]:λ1=1.804 6,λ2=0.768 3,λ3=0.427 1,
R2的特征根为:λ1=3.094 9,λ2=1.519 5,λ3=0.185 6,λ4=0,λ5=0,
R3的特征根为:λ1=1.612 0,λ2=1.385 2,λ3=0.002 8,

5)由式(5)~(7)求方差贡献率,确定主成分个数并进行主成分的综合评价。
R1的主成分为λ1=1.804 6,λ2=0.768 3,累计方差贡献率为85.76%;R2的主成分为λ1=3.294 9,λ2=1.519 5,累计方差贡献率为96.3%;R3的主成分为λ1=1.612 0,λ2=1.385 2,累计方差贡献率为99.91%。主成分的综合评价值如表2~4所示。
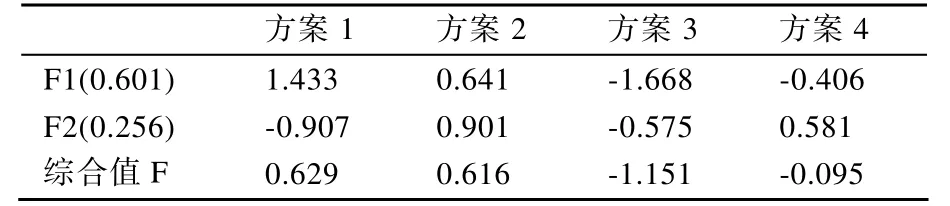
表2 C1指标综合评价值
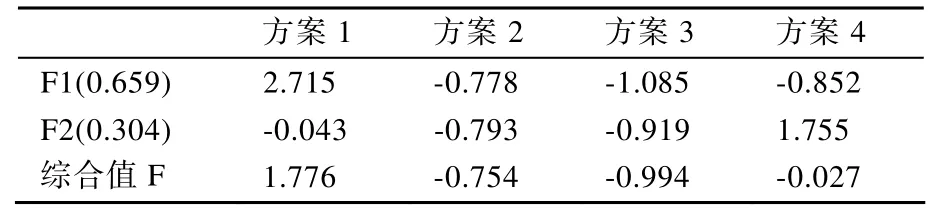
表3 C2指标综合评价值

表4 C3指标综合评价值
6)将二级指标进行综合得出最终总体评价值。
总体评价值如表5所示。从表5的最终结果大小排序可知,4种保障性方案中,需要注重改进的顺序依次为方案1、方案2、方案4、方案3。因此,从好到差的顺序依次为方案3、方案4、方案2、方案1,方案3的保障性最好。从评价结果来看,其结果较为合理客观,符合武器系统综合保障的实际情况,为综合保障决策提供了一定的依据。
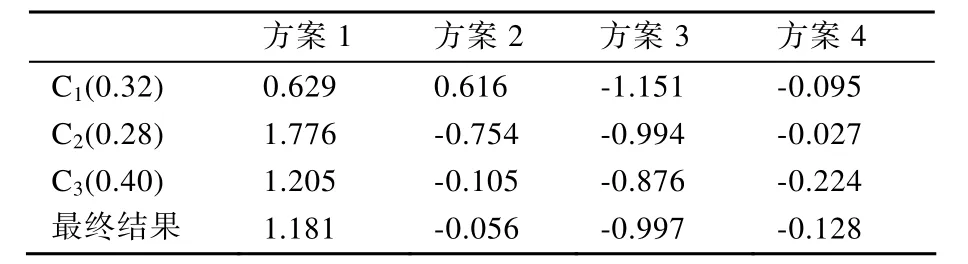
表5 某武器系统综合评价结果
4 结束语
本文给出了一种用主成分分析法解决武器系统保障性评价问题的可行方法,并在传统主成分分析法的基础上进行了改进,使得最终的评价结果在满足主观要求的基础上符合客观实际,为相似系统的评价问题提供了借鉴。
[1]徐廷学.装备综合保障工程理论与方法[M].北京:兵器工业出版社,2009:6-9.
[2]徐宗昌.保障性工程[M].北京:兵器工业出版社,2002:402-403.
[3]王明涛.多指标综合评价中权系数确定的一种综合分析方法[J].系统工程,1999,17(2):56-57.
[4]佟春生,畅建霞,王义民.系统工程的理论与方法概论[M].北京:国防工业出版社,2005:185.
[5]洪利华,罗均平,刘已斌.基于主成分分析法的目标威胁评估[J].指挥控制与仿真,2006,28(2):49-52.
[6]唐忠华.主成分分析法在导弹攻击目标优选中的应用[J].徐州工程学院学报,2006,21(3):65-67.
[7]袁洪涛,冯振声,王钰,等.装甲装备维修保障能力评估初探[J].兵工学报:坦克装甲车与发动机分册,2000(3):59-64.
[8]唐雪松,郭立红,陈长喜.基于AHP的威胁评估与排序模型研究[J].微计算机信息,2006,22(9):35-38.
[9]蒲俊,吉家锋,伊良忠.MATLAB 6.0数学手册[K].上海:浦东电子出版社,2002:47-48.
