湿空气掠过竖直壁面的凝结换热研究
2011-03-23李俊明王补宣
李 成,李俊明,王补宣
(清华大学 热科学与动力工程教育部重点实验室,北京 100084)
湿空气相变广泛存在于各种工业和民用设备中,石油化工、材料除湿、HVAC系统、冷却塔乏汽处理和锅炉烟气回收等领域.其中,湿空气凝结包括传热和传质同时发生的传递过程[1],如空调和化工用换热器[2]、除湿的显热和潜热分析[3-4]等一直被广泛关注.由于各种应用场合被处理的湿空气温度、含湿量以及壁面温度不同,凝结质量传递特点不同,但在换热器研究领域,采用计算及简化的方法[3-7]还没有统一性认识.
湿空气凝结是一种复杂的热量和质量传递过程.一般认为当湿空气遇到低于其露点温度的环境时,就会有水蒸气发生凝结.G.Comini和S.Savino[3]通过理论分析的方法讨论了水蒸气发生凝结的条件,认为由于气液界面表面张力的作用,需要很大的过冷度才能在空间发生凝结.根据Young-Laplace方程[4]也可以看出,由于凝结核很小,相界面的气、液两侧需要很大的压差才发生凝结.然而,由于凝结液滴和固体壁面之间的表面张力作用,凝结液滴会在壁面铺展,使得凝结核的曲率半径变大,在较小压差下凝结能够持续发生.因此,水蒸气的凝结过程可以分成如下2个过程[3],湿空气首先与冷壁面接触的温降过程,当温度降到露点温度以下时,壁面开始发生凝结.任能等[5]在平翅片换热器的数值研究中将凝结问题描述成水蒸气的“壁面反应”,忽略凝结液膜的影响,计算的传热系数实验的对比发现偏差为6%.数值计算 时,对凝结计算模型的处理常常假设为壁面膜状凝结.实际上,由于平板的表面并不满足均匀平整,各处的表面张力不同,完全的分层流动很难发生.
基于上述分析,在对湿空气流过竖直表面建立计算模型的基础上,分析忽略凝结液的合理性,比较水蒸气的3种凝结计算关联式并探讨它们的适用范围,讨论传质中影响对流传质的因素和对流传质在传质中的作用.
1 湿空气凝结特点
湿空气凝结是一种复杂的热量和质量传递过程.一般认为当湿空气遇到低于其露点温度的环境时,就会有水蒸气发生凝结.Comini和Savino[3]通过理论分析讨论了水蒸气发生凝结的条件,认为由于气液界面表面张力的作用,需要很大过冷度才能在空间发生凝结.
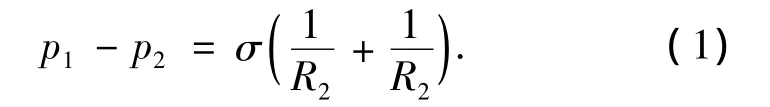
式中:p为压力,Pa;R为相界面的曲率半径,m;σ为表面张力,N·s-1.
从式(1)Young-Laplace方程[4]可以看出,由于凝结核很小,曲率半径较小,相界面气、液两侧需要很大压差才发生凝结.然而,由于凝结液滴和固体壁面之间的表面张力作用,凝结液滴会在壁面铺展,使得凝结核的曲率半径变大,需要较小压差凝结就会发生.因此,水蒸气的凝结过程可以分成如下2个过程[3]:湿空气首先与冷壁面接触的温降过程,当温度降到空气露点温度以下时,壁面上水蒸气开始凝结.任能等[5]在数值研究中把平翅片结构翅片管式换热器的凝结问题描述成水蒸气的“壁面反应”,忽略凝结液膜的影响,计算的传热系数实验结果比较发现偏差为6%.

式中:m为水蒸气凝结速率,kg·m-2·s-1;pv,a为水蒸气的分压力,Pa;pv,sat为水蒸气的饱和分压力,Pa.

式中:n为垂直壁面的法向方向,下角标i为相界面.

计算气液界面处的质量传递主要有3种方法:墙壁面[5-6]在夏季环境下凝结的计算关联式(2);采用水蒸气界面处扩散作用[7]的计算式(3);考虑浓度边界层对流作用 的质量流密度计算关联式(4).
数值计算[7-9]时,对湿空气凝结建立模型时,常将凝结液形态假设为壁面膜状凝结.实际上,由于平壁表面并不满足均匀平整,各处的表面张力不同,完全的分层流动很难发生,图1为实验观察的普通铝箔竖直表面的湿空气凝结,观察发现凝结液能很好的润湿壁面,而且有凝结液滴均匀分布在壁面上.

图1 湿空气在竖直表面的凝结Fig.1 Condensation of humid air on a vertical wall
可以看出,凝结过程不是珠状凝结,因为凝结液滴铺展的同时,会在表面张力作用下随机靠拢,并且在表面张力和重力的平衡被打破后局部下滑、脱落.Min等[10]对12种铜、铝表面的水蒸气凝结进行了实验观察,发现水蒸气在几种典型的翅片材料上凝结时,各种液滴滑落的后退接触角是决定凝结液以液滴形式滞留在平板表面的决定因素.
综上,膜状凝结并不能从本质上表征湿空气在竖直表面凝结换热规律,而目前对湿空气非膜状凝结的数值计算还比较困难,通过数值计算与实验对比发现[5],假设湿空气凝结液膜的厚度很小(一般小于0.127 mm[2]),热阻可以忽略不计.数值计算忽略凝结液的存在,不采用膜状凝结假设.
基于上述讨论分析,在对湿空气流过竖直冷壁面建立计算模型基础上,分析忽略凝结液的合理性,比较水蒸气的3种凝结计算关联式并探讨它们的适用范围,讨论传质中影响对流传质的因素和对流传质在传质中的作用.
2 计算模型及数值计算方法
如图2所示的二维的数值计算模型,空气以一定流速、温度和相对湿度流过竖直冷表面的二维、稳定层流流动.鉴于实际的凝结液形态复杂性和凝结液的热阻很小的特点[5,11],忽略凝结液的存在、气液界面处的流速滑移和温度阶越.

图2 计算区域及网格Fig.2 Numerical region and meshes
2.1 控制方程描述

式中:u为x方向速度分量,m·s-1;v为y方向速度分量,m·s-1.
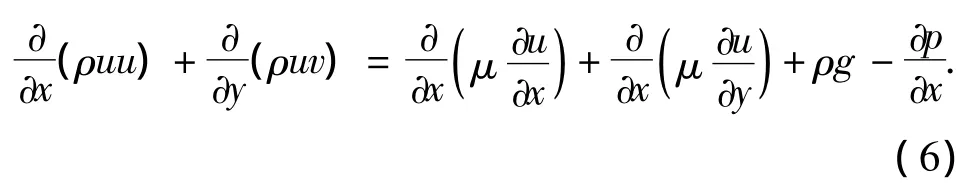
式中:g为重力加速度,m·s-2.

式中:cp为定压比,J·kg-1·K-1;k为湿空气的导热系数,W·m-2·s-1.

式中:w为湿空气中水蒸气的质量分数;D为止扩散系数,m2·s-1.
忽略凝结液的影响后,控制方程为湿空气的连续性方程(5)、动量方程(6)和(7)、能量方程(8)和组分输运方程(9).
2.2 边界条件
在入口处x=0.1 m和对称边界处y=0.05 m:

在出口处x=0.1 m:

在y=0处:
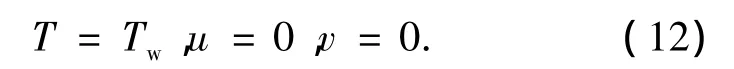
如图2所示,计算区域的宽度为y=0.05 m,长度x=0.1 m;入口和对称边界(10)为均匀恒定的速度、温度和浓度,湿空气流动方向平行于壁面.出口条件如式(11)所示,温度梯度和浓度梯度沿湿空气流动方向为零.壁面条件如式(12)所示,气液界面处为无滑移流速边界条件,冷壁面温度均匀恒定;水蒸气的凝结速率采用式(4)计算.
2.3 物性参数
密度ρ=353.0/T-141.86·x/T kg·m-3,动力粘度μ=1.804×10-5kg·m-1·s-1,扩散系数D= 2.45×10-5m2·s-1,普朗特数Pr=0.722,定压比热 cp=1.027 kJ·kg-1·K-1,导热系数 k= 2.566×10-2W·m-1· K-1,气 化 潜 热 Hv= 2 478 kJ·kg-1,施密特数Sc=0.605.
为便于和已有结论对比,除密度外,本计算过程中物性参数按文献[3]取得.
2.4 数值计算方法
计算区域及网格划分情况如图2所示,网格划分的原则按照越靠近冷壁面和入口越密集的非结构化网格,认为当网格疏密对冷壁面Nu数相对影响小于0.5%时的最稀疏网格为最佳.根据上述原则,对756、2 478、7 356、18 325和45 256单元数为对象,Nu结果表明当网格的单元数为7 356个时,网格数量加密对热流量的变化满足误差要求.计算采用的网格单元数为7 356个.数值计算借助商用CFD软件Fluent求解.
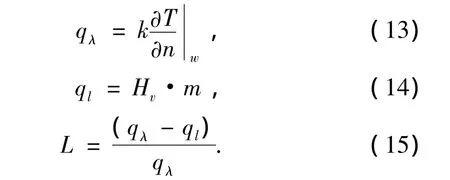
计算过程首先根据假设的初始条件和边界条件求解连续性方程和动量方程,然后依次求解温度场和浓度场;由于计算过程中水蒸气在冷壁面发生凝结,在处理方法上根据式(4)求得水蒸气的凝结速率,在Fluent中将其作冷壁面处的质量源,该边界的质量源受条件(14)的约束.下一次计算时,将质量源添加进去,作为下一步迭代求解的附加条件.当连续性方程、流速、温度和浓度的迭代残差都小于10-9时认为计算结果收敛.然后根据质量和能量守恒分别对湿空气进、出口和冷壁面处的质量和热量传递验证.
壁面处的总换热量可根据无滑移边界的冷壁面处傅里叶定律(13)求得,水蒸气凝结引起的潜热换热量根据式(14)进行计算,可得冷壁面对流热量与总热量之比,如式(15)所示.
3 计算结果分析
3.1 计算结果验证
3.1.1 入口温度和质量分数对L值影响的验证
图3所示为各种入口温度条件下L值随湿空气入口质量分数的变化关系,计算结果与Comini[3]推导的热、质传递类比模型(16)进行对比.从图3可以看出,数值计算结果与热、质传递类比模型(16)吻合较好,略高于的原因在于数值计算中忽略了凝结液膜,并且在凝结表面采用无滑移边界条件,使得热量传递速率偏低.数值计算结果与类比理论解相比的最大误差在1.2%以内.可以看出忽略凝结液膜对L值的影响不大.


图3 win和Tin对L值的影响Fig.3 Effect of winand Tinon L
3.1.2 水蒸气凝结量验证及对计算公式分析
根据式(2)~(4)和(17)计算得到水蒸气凝结量如图4所示,可见采用式(2)计算的水蒸气凝结量偏低,并且随着入口流速的增加而增大.Lucas等[6]将式(2)用于计算湿空气竖直墙表面凝结时,计算结果吻合较好,而任和谷[5]用计算强制对流凝结时,结果与实验误差相差6%,可见式(2)用于计算自然对流时较好,但不能很好预测强制对流下湿空气凝结速率.式(3)、(4)和(17)分别计算的结果比较接近,式(3)和(16)误差不到1.3%,式(4)和式(17)完全吻合,误差在1%以内.其中式(17)根据层流温度和浓度边界层理论得出的经典关系式.从图3和图4可见,第2章所建立的数值计算方法的热、质比与经典理论吻合较好,水蒸气凝结量与式(17)误差也较小,所以根据潜热换热量和热质类比可以推算,数值计算中对流换热量的计算结果也必然相差不大.


图4 uin对凝结速率的影响Fig.4 Effect of uinon condensation flux
3.1.3 入口流速对传质传递的验证
图5为L值随流速的变化,可以看出随入口流速的增加L略有增加,但变化很小,认为流速对显热和潜热之比的影响很小.而式(16)中显热和潜热之比与流速无关.在我们所研究范围内的流速从0.5 m·s-1到4.0 m·s-1的较大范围内变化时,L值仅增加了0.83%.数值计算结果与式(17)相一致,最大误差为1%.

图5 uin对L值的影响Fig.5 Effect of uinon L
3.2 L值x方向的发展特点
图6为湿空气流过竖直壁面时,从湿空气入口沿着x方向L值的变化特点.

图6 壁面上热质类比的特点Fig.6 Analogy of heat and mass transfer along the wall
从图中可以看出,在靠近入口处L值变化梯度很大,而在入口的尖端处浓度边界层和温度流速边界层的发展都不遵循边界层理论,此时入口附近L值变化较大.根据数值计算中Le等于0.838,当距入口一定位置后,沿壁面法向浓度边界层与温度边界层、壁面处温度梯度和浓度梯度满足相似关系.因此,显热和潜热的换热量比值趋于一定.从图6也可以看出,随着x距离增加,L值的变化很小,并趋于稳定.
3.3 影响界面处对流传质速率的因素
湿空气凝结的界面处,水蒸气的法向流速vn并不为0,因为水蒸气会穿过界面发生对流传质[7],对流传质凝结速率如式(18),相界面处法相流速vn具体推导过程请参考文献[7].对流传质量(18)和扩散传质量(3)之和为凝结过程的总传质量(4).相界面法相速度公式(19)可知,影响对流传质的因素是气液界面处的法向浓度梯度和凝结壁面的浓度大小.

3.3.1 入口流速对wn的影响
图7为vn随入口流速和壁面位置之间的变化关系.可以看出当温度一定时,冷壁面不同位置vn的大小不同,越靠近入口前端,法向流速vn越大,而随着与入口距离增加,vn先逐渐变小,然后趋于平稳.原因是在冷壁面前端的浓度边界层较薄,浓度梯度较大,对流流速也较大,随着距离冷壁面前端距离的增加,浓度边界层厚度逐渐增加,界面处的浓度梯度减小,由式(19)可知vn沿流动方向逐渐减小.而且从图7可以看出随着入口流速的增加vn增大.在入口流速较小时,vn随入口流速的增加而增大的较快,当流速增加到2.5 m·s-1时入口流速的变化对vn的影响很小.主要因为增加流速能使浓度边界层变薄、界面处浓度梯度变大.

图7 壁面上uin对vn的影响Fig.7 Effect of uinon vnvalues along the wall
3.3.2 入口质量浓度对vn的影响
图8为入口水蒸气的质量浓度对界面法向流速vn的影响.对比图7和图8可以看出,水蒸气的来流质量分数对vn的影响与入口风速对vn的影响有相似变化趋势.主要因为随着水蒸气来流质量浓度的增加,界面处的浓度梯度增大.沿着湿空气流动方向浓度边界层的发展逐渐变厚,界面处浓度梯度变小.

图8 壁面上win对vn的影响Fig.8 Effect of winon vnalong the wall
3.3.3 壁面温度对vn的影响
如式(19)所示,壁面温度对vn的影响表现在温度场对界面浓度梯度的影响和壁面处水蒸气的质量浓度.从图9可以看出vn随着壁面温度增加逐渐减小,而且壁面温度较高时,温度的变化对vn的影响较大.这主要因为壁面温度高时,壁面处水蒸气的质量分数大,从而对流传质的速度变大的较明显.

图9 壁面上Tw对vn的影响Fig.9 Effect of Twon vnalong the wall
3.4 对流传质分析
由3可知,壁面处水蒸气质量浓度对vn影响较大,而相界面处水蒸气的质量浓度直接受壁面温度的影响.图10为对流传质的占总传质量的分额随壁面温度的变化关系.可见,壁面温度是影响对流传质的主要因素之一.壁面温度越高,界面处水蒸气的质量分数越大,界面法向速度vn越大,对流传质的比例值越大.从图10可以看出,当壁面温度小于300 K时,对流传质量的比例占传质量的比例不到2.5%,随着壁面温度的增加,对流传质的比例呈指数增加,当温度增加到310 K时,对流传质比例约占5%,而当温度增加到325 K时,对流传质比例增加到8%左右,此时,如果忽略对流传质的影响必定会产生很大的误差.

图10 Tw对对流传质比例的影响Fig.10 Effect of Twon advective mass transfer fraction
此外,入口温度、浓度和流速对扩散传质和对流传质的影响,表现在浓度边界层发展产生的界面处浓度梯度的变化.在所研究的范围,它们对扩散传质和对流传质比值的影响很小,因此对L值的影响也很小,数值结果中没有详尽讨论这部分内容.
综上,式(3)只适用于壁面温度较低的湿空气凝结设备,如空调用蒸发器领域;而当壁面温度较高时,热、质传递类比[12]规律发生变化,如果忽略界面法向流速vn对传质的影响将产生较大的误差,此时式(3)不再适用,而应用综合考虑扩散和对流传质的式(4)进行计算,如锅炉的烟气尾气热回收和冷却塔等.
4 结论
借助商用CFD软件Fluent,在详细分析水蒸气凝结特点的基础上,对竖直平壁建立控制方程并确定边界条件,验证了计算网格的无关性;根据湿空气凝结特点和学者们在数值计算时选用的相应模型进行探讨和分析,得出如下结论:
1)由于湿空气的凝结液膜一般不大于0.127 mm,在所研究几何尺寸范围内,忽略凝结液滴的对流传质与理论公式相比误差不大于1%.
2)计算湿空气凝结时,式(2)~(4)适用范围不同.式(2)不适用于强制对流情况,式(3)适用在扩散传质为主要质量传递的领域,因此在计算低温壁面的湿空气凝结速率时较适用,当壁温较高时不再适用,此时对流传质作用不容忽略,而应采用公式(4)进行计算.
3)通过分析入口的温度、浓度和流速以及壁面温度对界面法向速度的影响,发现随着入口流速的增加vn逐渐增大,速度的变化对vn的影响逐渐减小;随着入口浓度的增加vn逐渐增加;随着壁面温度的增加vn逐渐减小,壁温越高vn越大.
4)分析对流传质的影响因素发现,冷壁面温度是影响对流传质在传质中比例的主要因素.当壁面的温度大于310 K时,忽略对流传质的对传质影响将引起超过5%的误差,并且随着冷壁面温度的增加,对流传质的作用越大,误差也会越大因此,在涉及湿空气凝结的不同工业领域,对流传质所起的作用不同.
[1]KRZYSTOF W,GRAZYNA B,MARTELMUS M B.Modeling of countercurrent partial condensers for light hydrocarbon streams containing hydrogen[J].Chemical Engineering and Processing,1998,37(5):389-403.
[2]THRELKELD J L.Thermal environmental engineering[M].Englewood Cliffs:Prentice-Hall,1970:263-267.
[3]COMINI G,SAVINO S.Latent and sensible heat transfer in air-cooling applications[J].International Journal of Numerical Methods for Heat and Fluid Flow,2007,17(6): 608-617.
[4]GHIAASIAAN S M.Two-phase flow,Boiling and condensation[M].New York:Cambridge University Press,2008: 39-41.
[5]任能,谷波.湿工况下平翅片传热传质实验与数值模拟[J].化工学报,2007,58(7):1626-1631.
REN Neng,GU Bo.Experimental study and numerical simulation of heat and mass transfer on plain fin in wet conditions[J].Journal of Chemical Industry and Engineering,2007,58(7):1626-1631.
[6]LUCAS F,ADELARD L,GRADE F.Study of moisture in buildings for hot humid climates[J].Energy and Buildings,2002,34(4):345-355.
[7]SRZIC V,SOLIMAN H M,ORMISTON S J.Analysis of laminar mixed-convection condensation on isothermal plates using the full boundary-layer equations:mixtures of a vapor and a lighter gas[J].International Journal of Heat and Mass Transfer,1999,42(4):685-695.
[8]HUANG C C,YAN W M,JANG J H.Laminar mixed convection heat and mass transfer in vertical rectangular ducts with film evaporation and condensation[J].International Journal of Heat and Mass Transfer,2005,48(9):1772-1784.
[9]SIOW E C,ORMISTON S J,SOLIMAN H M.Two-phase modeling of laminar film condensation from vapor-gas mixtures in declining parallel-plate channels[J].International Journal of Thermal Sciences,2007,46(5):456-466.
[10]MIN J C,WEBB R L.Condensate formation and drainage on typical fin materials[J],Experimental Thermal and Fluid Science,2001,25(3-4):101-111.
[11]VOLCHKOV E P,TEREKHOV V V,TEREKHOV V I.A numerical study of boundary-layer heat and mass transfer in a forced flow of humid air with surface steam condensation[J].International Journal of Heat and Mass Transfer,2004,47(67):1473-1481.
[12]SHANG D Y,ZHONG L C.Extensive study on laminar free film condensation from vapor-gas mixture[J].International Journal of Heat and Mass Transfer,2008,51(17/ 18):4300-4314.
