弹簧-质点模型中弹簧力计算问题

许 红,许浩然

(武汉理工大学大学物流工程学院,湖北 武汉 430063)

质点-弹簧模型是一个重要的物理模型.作为一个具有刚性系数、长度、不考虑其本身质量的抽象体,弹簧发生形变常会使与之相连物体的受力、加速度、速度、动能等物理量发生变化.借助于弹簧的变化来分析物体的变化渗透到中学物理教学的许多领域,对这类系统的分析常遵守牛顿运动定律、功能关系等,因常伴随着动态变化,使此类题型的难度较大.本文将以双质点-弹簧模型为例,就此类问题进行一定的分析和求解.

1 质点-弹簧模型

为了便于研究复杂的质点-弹簧模型,在传统单一质点-弹簧模型的基础上考虑双质点-弹簧模型.现对此双质点-弹簧模型中的各字母参数的意义做如下描述:m0为质点1的等效质量;m1为质点2的等效质量,该质点附着在质点1上;m2为质点3的等效质量;X为等效质量为m0+m1的位移;X2为等效质量为m2的位移;g为重力加速度;K为弹簧1的刚度系数;K2为弹簧2的刚度系数.

为便于求解,附加如下条件[1-2]:1)质点2附着在质点1上,二者并没有相对变形,设为刚性质点;2)弹簧1的刚度系数K相对较大,在整个系统运动过程中变形较小.

2 质点-弹簧模型中弹簧力计算

2.1 质点起升时弹簧力的计算

对质量分离体(m0+m1)和m2进行分析,计算模型如图1所示.

图1 弹簧-质点模型

由牛顿第二定律得等效质量(m0+m1)的微分方程

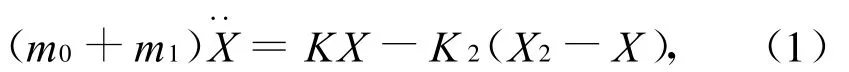
等效质量m2的微分方程

这里主要研究质点起升时弹簧的形变及其拉力,故弹簧形变引起的拉力P=KX,则由式(2)×(m0+m1)-式(1)×m2得到:

化为标准微分方程:

方程(4)的通解为

将式(6)代入方程(4)对比可知:

则方程(4)的通解为

当t=0时,(X1-X)0=m2g,(﹒X2-﹒X)0=0,代入式(1)求得:

综上,方程(4)的通解为

则此时弹簧的弹性力

2.2 质点起下降时弹簧力的计算

假设质点以稳定速度上升,这时弹簧系统承受质点的静力作用.假设阻力pT作用在质量m0+m1上,显然,这种情况下,其加速度方向和预张紧过程相反,其初始条件和预张紧型启动过程的一样.计算方法同2.1部分,该条件下弹簧的弹性力

3 结论

弹簧的弹力是由形变而决定大小和方向的,对于该习题的求解一般要从弹簧的形变分析入手,找出形变量和物体空间位置变化的几何关系,以此分析形变所对应的弹力大小和方向.此外,双质点-弹簧模型在实际生活中应用较为广泛,许多工程实例都可以转化为质点-弹簧模型.

[1]Zhang Zhengyan,Chen Dingfang,Feng Min.Dynamics model and dynamic simulation of overhead crane load swing systems based on the ADAMS[C]//The 9th International Conference on Computer-aided Industrial Design&Conceptual Design.2008:484-487.

[1]Xiao FengMin,Lu Han-bin,,Zhang Shi-qing,et al.Dynamics simulation analysis of bridge crane hoisting mechanism based on ADAMS[C]//ICMET2009.2009:93-98.