基于GMM微进给刀架的温度特性分析

陈天沛,余 震,李勇智,陈定方

(1武汉理工大学智能制造与控制研究所,湖北 武汉 430063;2武汉科技大学机械自动化学院,湖北 武汉 430081)

超磁致伸缩材料(GMM)是一种新型高效的磁能—机械能转换材料[1],利用超磁致伸缩材料在磁场变化时发生伸缩形变而制作的超磁致伸缩致动器,具有输出力大、位移分辨率高、响应快等诸多优点[2],已在精密加工、超精密加工领域显示出广阔的应用前景.然而超磁致伸缩驱动器在工作时,驱动线圈的发热、超磁致伸缩棒的磁致损耗等均可导致超磁致伸缩棒温度升高,而温度对超磁致伸缩材料的伸缩特性影响很大[3].因此,设计制作超磁致伸缩驱动器(Giant Magnetostrictive Actuator,GMA)时,必须考虑温升对驱动器输出精度的影响.本文在分析GMA发热源及温升对GMA输出精度的不利影响基础上,针对长时间工作条件下的某微进给平台中的GMA,分别在无水冷以及强制水冷两种条件下进行有限元瞬态热分析.根据有限元分析结果,进一步指导GMA参数设计.

1 温升对超磁致伸缩致动器的影响

1.1 超磁致致动器工作原理及热源

超磁致致动器的结构如图1所示.其工作原理为:当电磁线圈3内通入适当大小的电流时,将产生一个驱动磁场;在驱动磁场作用下,GMM棒6发生形变,推动输出轴7运动,产生输出位移和输出力,将电磁能转化为机械能.

超磁致致动器的发热源主要有电磁线圈通电后发热、涡流与动态工作中的磁滞效应等[4].

图1 磁致伸缩微致动器结构

1.2 温升对超磁致伸缩致动器的影响

超磁致伸缩致动器的核心部件GMM棒发热后会对其输出精度产生影响,主要表现为以下几个方面.

1)温升引起GMA各部件的热膨胀.线圈发热导致的温升将导致GMA系统内各部件尤其是GMM 棒的热变形.其热变形量

2)导致磁致伸缩系数不稳定.超磁致伸缩材料的磁致伸缩系数对温度很敏感.图2为在13.8 MPa预压力下温度对超磁致材料磁致伸缩率λ的影响[5].

由图2可知:温度在40℃以下时,磁致伸缩率λ随温度上升而迅速增大;温度在40℃～50℃之间,磁致伸缩率λ较为稳定;温度超过50℃时,磁致伸缩率λ随温度上升而缓慢减小.以图中磁场强度为2000 Oe为例,温度在 20℃和30℃时,其磁致伸缩率λ分别为1.1×10-3和1.3×10-3,由此导致相同磁场激励下GMA输出差异达20%.

3)引起壳体及其它部件热膨胀.电磁线圈工作产生的热量,不仅影响GMM棒,也会由棒表面及两个端面传向相接触的零件,导致壳体、输出轴及底座的热变形.

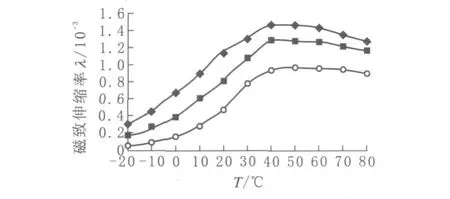
图2 温度对磁致伸缩系数的影响

2 基于ABAQUS超磁致致动器瞬态热分析

2.1 有限元建模及单元选取

一个完整的ABAQUS有限元分析过程包括以下三个基本步骤:前处理、分析计算及后处理.

要在ABAQUS软件环境下进行有限元分析,首先需要建立致动器的有限元模型.其过程主要包括:三维模型的建立、材料属性的赋予、零部件的装配以及网格划分.图3为在ABAQUS环境下本平台超磁致致动器的有限元模型.

图3 超磁致致动器的有限元模型

根据单元的轴对称性质,选取八结点线性传热六面体单元(DC3D8).该单元有8个节点,每个节点仅包含一个自由度,即温度.

2.2 热载荷及边界条件

热载荷是指热源单位体积的发热量,超磁致伸缩致动器所承受的热载荷主要为线圈的热载荷,计算公式为:

式中:Q为线圈的发热量,W;V为线圈的体积,m3.

对于线圈来说,发热量可以按照电阻发热的公式计算:式中:I为线圈中通入的电流,A;R为整个线圈的电阻,Ψ.

测得线圈电阻为 8.3 Ψ,通过电流为 1.8 A,计算得发热功率为26.892 W.根据式(2)计算得单位体积发热功率即热载荷约为95.58 kW/m3.

在分析时,热载荷q是以体载荷形式加载在线圈的模型上.由于主要的换热方式是超磁致伸缩致动器内部冷却水流动通过致动器时对流换热带走热量,同时致动器外部空气对流换热也会带走少部分热量,所以边界条件主要是考虑第三类边界条件,即空气与结构表面的自然对流换热以及恒温水与零部件之间的强制对流换热.此外,致动器的其他边界条件为:致动器初始温度为20°C,空气温度为室温 20°C,冷却水的温度设为恒温 19°C.

3 有限元分析结果及讨论

3.1 超磁致伸缩致动器无水冷的瞬态分析

当强制水冷装置不工作时,可以视为冷却水腔为空气的自然对流,在软件的Interaction模块中将Surface film condition中的Film Coefficient设为12.5.图4为利用ABAQUS进行有限元分析,得出的致动器工作0.5 h后整机的温度分布云图.

图4 无水冷时GMA温度云图

3.2 超磁致伸缩致动器强制水冷的瞬态分析

当强制水冷装置工作时,水冷腔内通入循环的恒温冷却水,腔内对流边界条件发生改变,在Interaction模块中将Surface film condition中Film Coefficient更改为400,其余参数相同.致动器工作0.5 h后,温度分布云图见图5.

图5 强制水冷时GM A温度云图

3.3 总结及讨论

从以上两组分析可以得出如下结论,强制恒温水冷可以有效地降低GMM棒的温升.两组GMA各部件的热分析结果如表1所示.

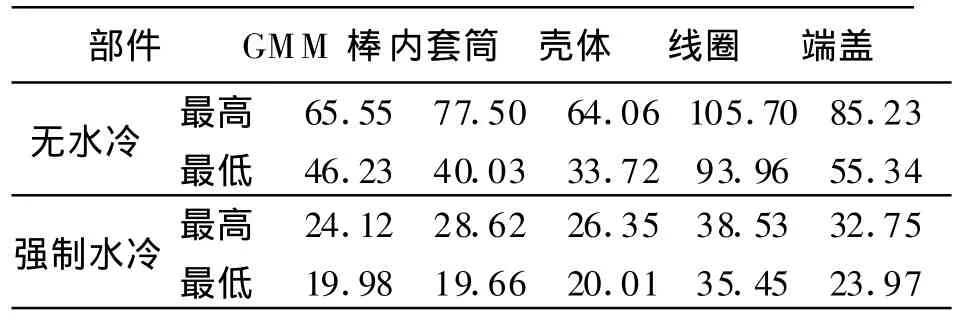
表1 两种工况下分析结果比较 ℃

在大功率、长时间工作场合,对于无水冷的超磁致伸缩致动器,GMM 棒最大温升为45.55°C,由式(1)可计算出GMM 棒热膨胀变形为 27.33 μ m.而所设计的驱动器输出为50 μ m.显然由GMM 棒温升导致的热膨胀将致使GMA输出精度大幅降低.此外,线圈的发热十分严重.而在相同工况下,带水冷装置的致动器,GMM棒温升只有4.12°C,GMM棒热变形为2.47 μ m,其热膨胀引起的变形降低了一个数量级,温控效果比较理想.

4 结束语

本文对超磁致驱动器在无水冷及强制水冷两种工况下进行有限元分析.分析结果表明,采用强制水冷可以有效地抑制致动器的温升.在大电流、长时间工作的场合中,超磁致伸缩致动器必须采取强制水冷的方式进行温控,以保证其输出精度和工作性能.

[1]Clark A E.Magnetostrictive Rare Earth-Fe2 Compounds[M].Amsterdam:North-Holland,1980.

[2]贾宇辉,谭久彬.基于超磁致伸缩材料的微位移驱动器特性研究[J].中国机械工程,1999,10(11)1213-1215.

[3]徐 杰,陈张健,邬义杰.超磁致伸缩驱动器热变形补偿及温控方法研究[J].设计与研究,2005(06):8-10,19.

[4]卢全国,陈定方,钟毓宁,等.超磁致伸缩致动器热变形影响及温控研究[J].中国机械工程,2007,18(1):16-19.

[5]Clark A E,Crowder D N.High Temperature Magnetostriction of TbFe2 and Tb.27 Dy.73 Fe2[J].IEEE Transactions on Magnetics,M AG.21,1985(5):1945-1947.