伺服运动系统控制参数在线调节算法研究
2011-03-23宋福民
方 强,宋福民
(深圳市大族数控科技有限公司,广东 深圳 518057)
伺服运动系统通常采用PID+前馈控制策略,具有鲁棒性强(对工况的适应能力强)、算法容易实现等优点,然而PID+前馈控制策略属于经典控制理论范畴,适合于线性控制系统,但是实际工程应用中往往受非线性、参数时变等不确定性因素的影响,导致控制效果不理想;此外由于参数整定直接受负载性能的影响,往往整定不良、性能欠佳,导致对运行工况(扰动、参数时变等)的适应性差。
伺服控制系统的基本结构如图1所示。
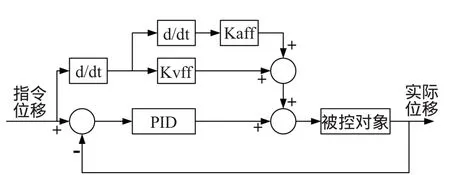
图1 伺服控制系统框图
伺服控制策略中,比例环节用于调节伺服运动系统的刚性,微分环节提供运动所需要的阻尼(改善系统动态性能),积分环节用于消除稳态误差,速度前馈环节用于减小由阻尼引起的跟随误差,加速度前馈环节用于减小由系统惯性带来的跟随误差。因此研究控制参数自适应控制算法对改善伺服运动系统性能具有重要意义。
首先提出了基于速度分段的控制参数整定原理和在线调节原理,再基于PMAC控制器开发控制参数在线调节算法程序,之后在实际PMAC伺服运动系统上验证了该算法的有效性。
1 控制参数分段整定算法
传统PID+前馈伺服控制算法,一旦控制参数整定完毕就被固定到控制器中,不能根据现场的变化进行适应性调整。通过对实际伺服运动系统跟随误差的测量发现当运动平台的速度和加速度发生改变时,跟随误差的波形随之变化,为此可以将运动平台的速度曲线划分为多个连续的小区间,然后分别对各个速度区间上的控制参数进行整定。
1.1 构建速度分段模型
伺服运动系统的轨迹规划方法通常有梯形曲线加减速和S曲线加减速两种。两种加减速曲线如图2所示。
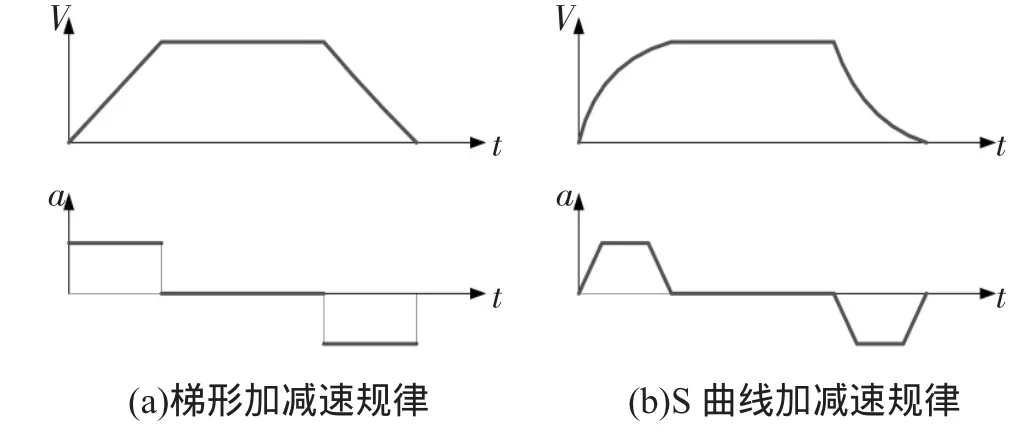
图2 伺服运动系统加减速曲线
从图2可以看出S曲线加减速规划相对于梯形曲线加减速规划,运动平台的速度变化平滑,减小了因加速度突变引起的冲击。以梯形指令速度曲线为例建立如图3所示的速度分段模型。
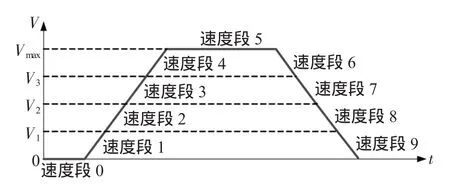
图3 速度分段模型
图中将指令速度曲线的静止段、匀速段划分为两个独立的速度段,将加速段和减速段分别划分为多个连续的速度段。考虑到反向运动,各个速度段具有如下特征:

说明:V和A分别为当前指令速度和指令加速度,V1、V2和V3为所划分的速度区间的端点速度(由用户对指令速度曲线进行划分后确定),Vmax为最大指令速度。
1.2 控制参数分段整定
在构建了速度分段模型后,可以通过采集各个速度段上的跟随误差数据,构建评价函数,经过多次试验整定出使评价函数值最小的控制参数。控制参数整定方法通常有人工整定和自整定两种方法,人工整定法依赖于调试人员的经验,具有一定的随意性、整定效率低、整定效果难以逼近最优,为此结合速度分段模型给出如下控制参数分段自整定方法,见图4。
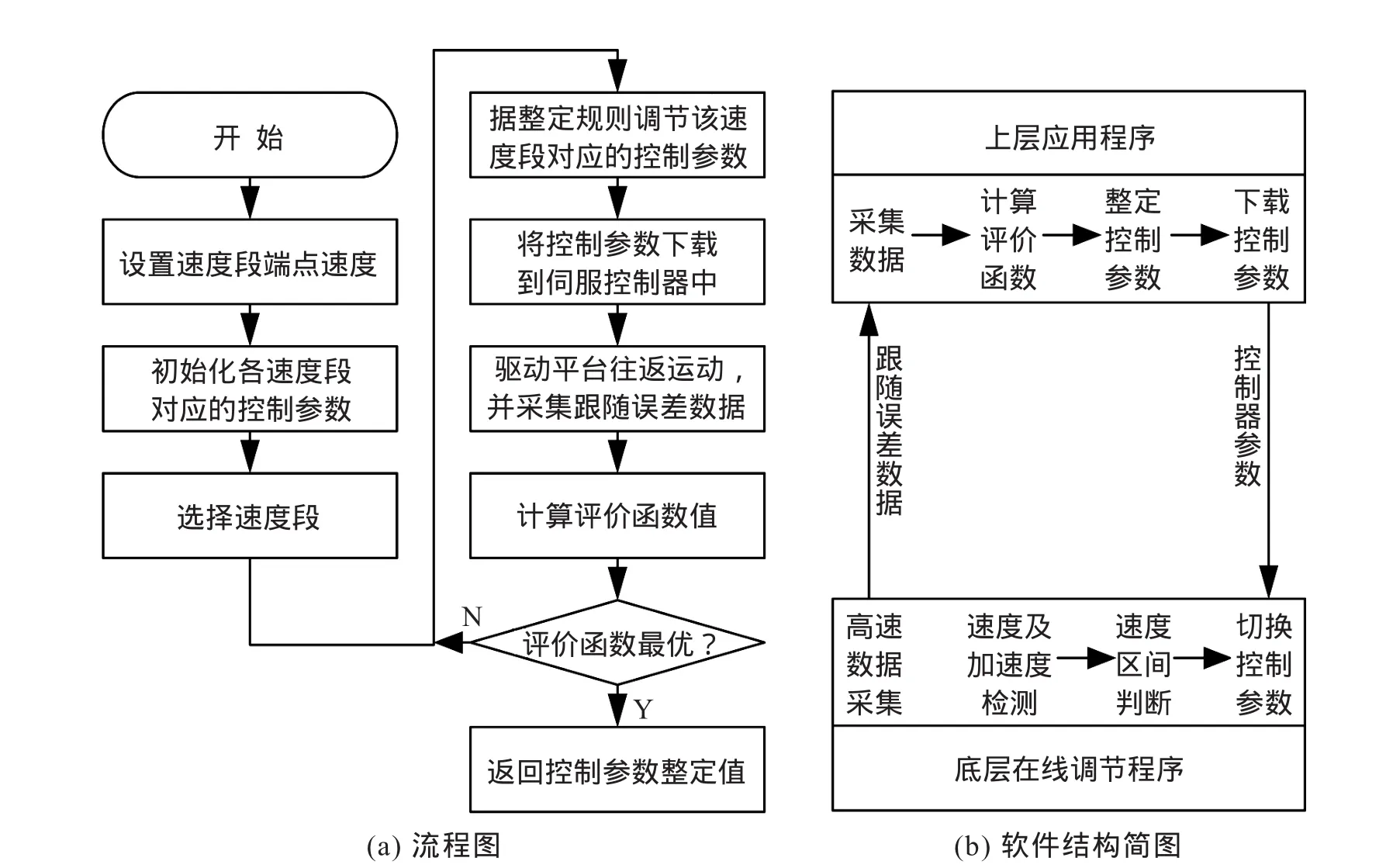
图4 控制参数分段自整定原理图
控制参数分段自整定不能由运动控制器的底层在线调节程序单独完成,否则受到数据采样、计算延迟等的影响会降低在线调节程序的实时性。在线调节程序只用于对指令速度和指令加速度进行在线监测,并根据速度分段模型切换控制参数,而控制参数的修改、跟随误差数据采集、控制参数寻优等功能需要由上层应用软件来完成。
控制参数分段自整定的关键在于研究合适的控制参数寻优算法,对于单个控制参数寻优算法很容易实现(通过单循环法搜索合适的控制参数,使得评价函数值最小),而对于多个控制参数的寻优,如果采用循环嵌套寻优法,则效率极低,且容易受循环步长影响。单纯形法是解决高维寻优的最优化方法,它不需要求导数,只要能够测量到系统的响应值就可以使用。
2 控制参数在线调节算法
控制参数在线调节就是根据速度分段模型,当指令速度落入相应的速度段,立即将控制器参数切换为该速度段上事先整定出的控制参数。由于速度段的区间较宽,避免了控制器参数的频繁切换,可以满足控制器在线调节程序实时性需要,见图5所示。
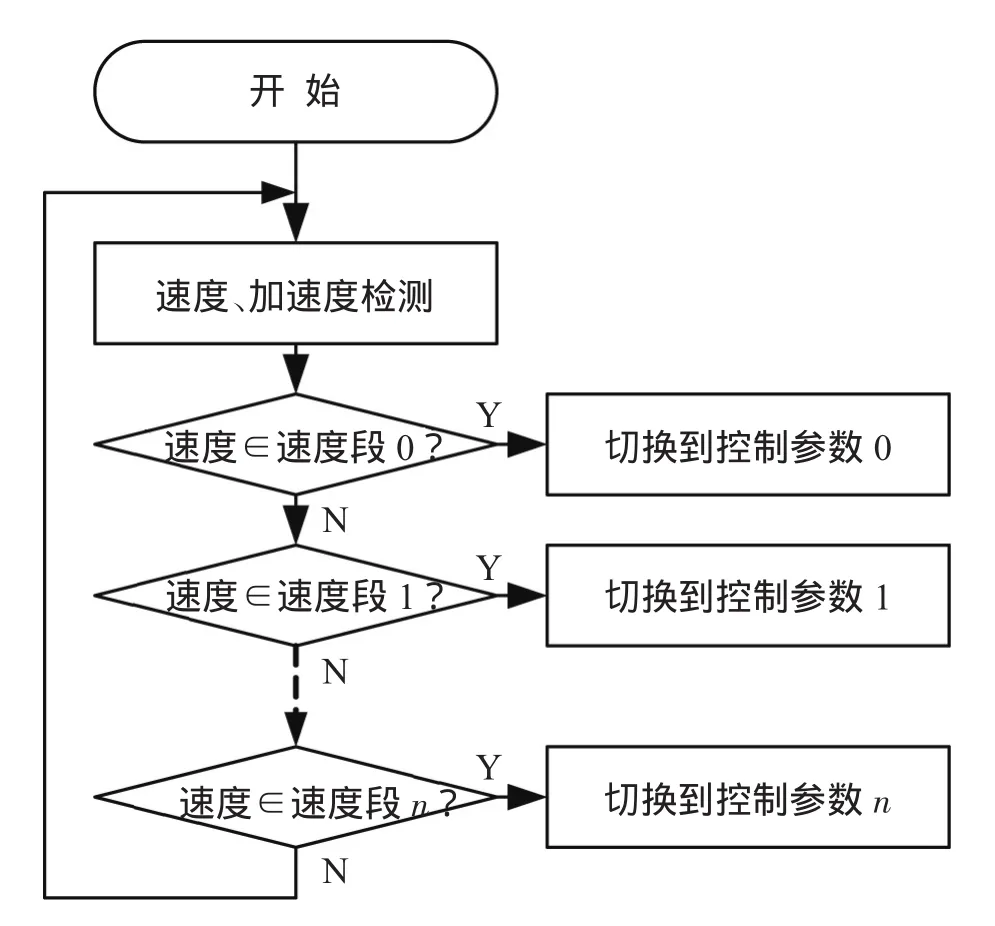
图5 控制参数在线调节流程图
3 算法实现
为了验证算法的有效性,以PMAC运动控制器为研究对象详细介绍算法的实现过程。PMAC控制器是Delta Tau公司生产的多轴运动控制器,能够对存储在它内部的程序进行单独运算,同时执行运动程序、PLC程序和伺服控制程序,而且可以自动对任务进行优先级判别,从而进行实时的多任务处理。
PMAC控制器参数的分段自整定与在线调节算法实现的基本思路是:利用PMAC控制器允许嵌入PLC程序的功能开发出用于速度分段和控制参数快速切换的PLC程序,基于PMAC控制器上的高速数据采集功能开发出上层应用程序,实现运动数据采集、评价函数计算、控制参数整定、控制参数下载等功能。
PLC程序实现如下功能:
(1)速度分段,即设定各个速度段的端点速度;
(2)指令速度、指令加速度在线监测;
(3)根据指令速度所处的速度区间实时切换控制参数。
上层应用程序实现如下功能:
(1)PMAC高速数据采集与解码;
(2)计算评价函数;
(3)控制参数(KP、KD、KAFF)整定(人工整定和自整定);
(4)下载控制参数到PMAC控制器中。
上层应用程序界面操作形式如图6、图7所示。
为了验证控制参数在线调节算法对改善系统动态性能的有效性,在PMAC控制器上嵌入控制参数在线调节PLC程序,结合上层应用程序整定出各个速度段上的加速度前馈增益值并测试出采用控制参数在线调节算法前后的跟踪误差曲线。
测试前先根据跟随误差变化情况建立速度分段模型(最大速度为160 cts/ms、最大加速度为1 cts/ms2),然后确定需要整定的控制参数的取值范围,最后对各个速度段上的控制参数进行整定(人工或自动整定)并下载到PMAC控制器中。测试曲线如图8所示。
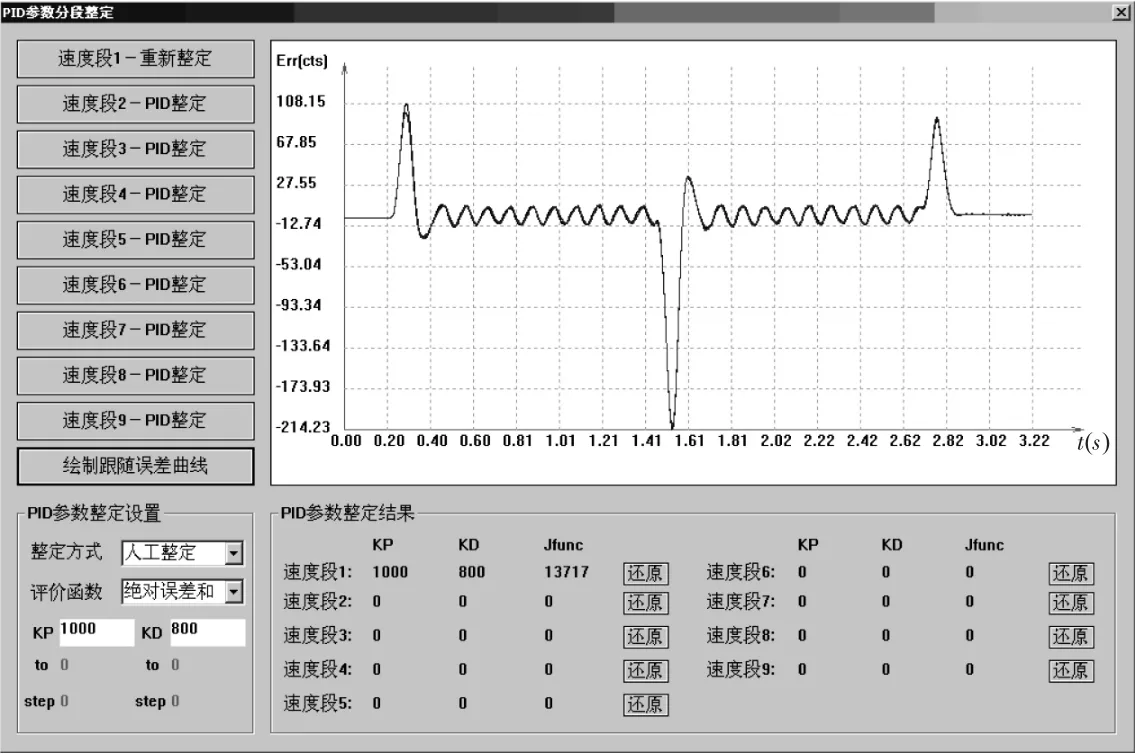
图6 PMAC控制器PID参数分段整定界面
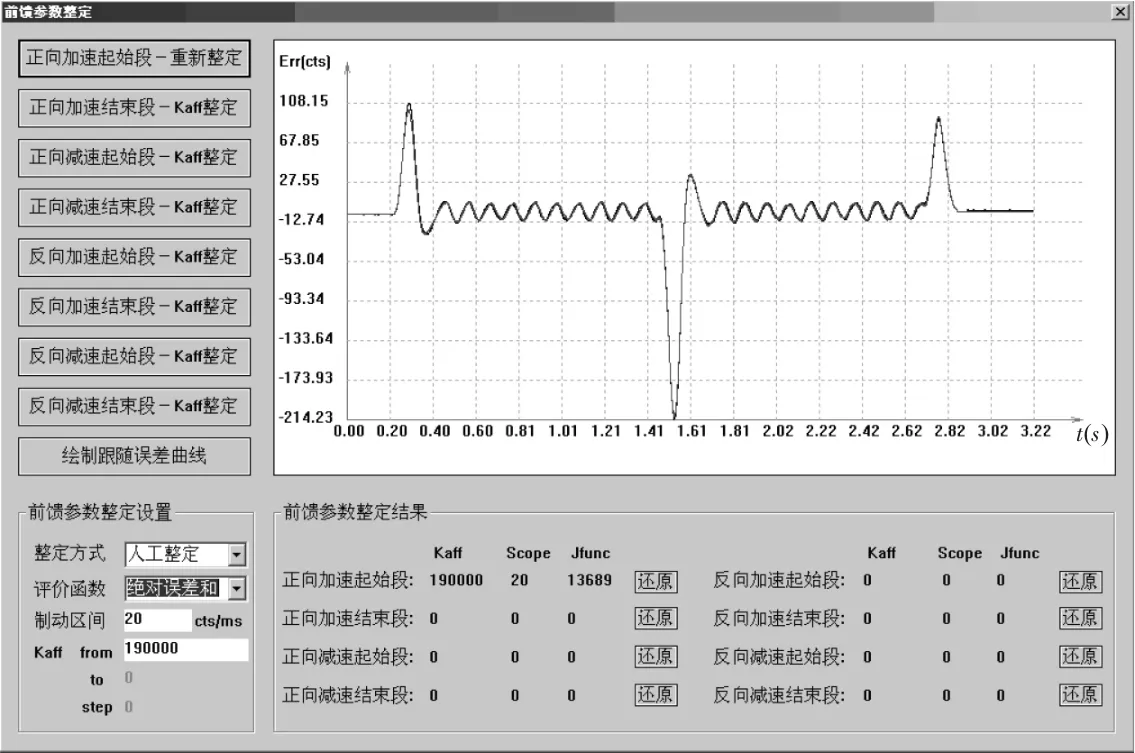
图7 PMAC控制器加速度前馈增益分段整定界面
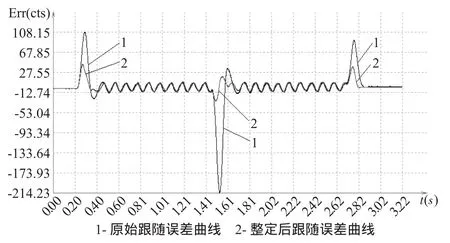
图8 系统定位运动实拍跟随误差曲线
4 结论
(1)伺服运动系统本身是一个惯性系统,加速度、驱动质量越大,惯性就越大,由此引起的跟随误差就越大,因此对加速度前馈增益进行在线调节,能明显改善系统的动态性能;
(2)受在线调节程序实时性的限制,控制参数分段自整定算法需要由底层实时控制程序和上层应用程序联合实现;
(3)控制参数整定,既可以对单个参数进行整定,也可以对多个参数联合整定,从而寻找出对改善伺服运动系统控制性能最有效的敏感参数;
(4)实现控制参数在线调节功能的前提是建立速度分段模型,因此划分合适的速度分段区间对改善伺服运动系统动态性能有明显影响;
(5)如果底层在线调节程序能够运行在最高优先级的伺服中断上(如TurboPMAC提供的开放伺服功能),则该算法能够应用到高速伺服运动系统中。
[1]杨更更,叶佩青,杨开明,等.基于PMAC的数控系统PID参数自适应调节[J].机械工程师2002(4):13-15.
[2]刘金琨.先进PID控制及其MATLAB仿真[M].北京:电子工业出版社,2003.
[3]陈玉霜,朱学峰,刘维之.简易单参数自适应PID控制研究[J].计算技术与自动化.2006,25(4):11-13.
[4]聂建华,李晟.基于前馈及自适应滤波的零跟踪误差伺服控制器[J].制造技术与机床,2007(9):109-112.
