基于复杂网络理论的时间序列分析

赵丽丽, 唐 镇, 王建勇, 王建波, 杨会杰

(1.上海理工大学管理学院,上海 200093;2.邢台学院物理系,邢台 054001)

物理理论是时间序列分析技术发展的一个基本源泉[1-3].物理学理论的每一个进步,往往首先被用于时间序列分析.混沌、分形、自组织临界、随机介质、少数者博弈理论等的发展,给时间序列分析注入了新的思想和技术手段,是非线性时间序列分析的理论和思想基础.复杂网络理论是近年来发展起来的统计物理的一个重要分支[4].一个复杂系统的诸多元素及其之间的关系,可以用复杂网络描述.网络的节点和边代表元素和它们之间的关系.复杂网络弱化元素之间的作用细节,而着重体现元素之间的相互作用关系的拓扑结构,从而凸显这种结构与复杂系统性质之间的关系.随着信息技术的发展,各个学科领域积累了海量的原始数据,从这些数据中提取复杂系统的信息,是当前的基本任务.复杂网络理论已经成为完成这一任务的最有希望的候选技术方法.实际上复杂网络理论已经成为很多学科发展的新视角和指导思想,如系统生物学[5].近年来一个活跃的研究课题是试图把复杂网络理论应用于时间序列分析,从复杂网络这一全新的视角出发,发展一套从时间序列映射到复杂网络的方法.期望能够提取到新的序列结构特征,从而深入认识复杂系统的结构和动力学机制.这些方法将应用于金融、生理医学、生物等序列分析中.

文献中已经建议了多种时间序列映射到复杂网络的方案,但是这些方法的有效性都是采用理论模型产生的标准序列验证的.当用于现实中的时间序列分析时,必须回答的问题包括:时间序列非定态对网络结构的影响、环境噪声和统计涨落对网络结构的影响及复杂网络能够提供哪些其它序列分析方法不能得到的性质.也就是复杂网络应用于序列分析的优势和局限性.笔者综述了当前时间序列复杂网络研究的进展,并对上述3个问题进行一些探索.

1 时间序列的复杂网络分析进展

文献[6-8]采用复杂网络理论对伪周期时间序列进行了分析.把序列的每一个周期片段映射成一个节点,如果两个周期片断的相空间距离或者相关系数满足一定条件,这两个序列片断对应的节点就相连,从而构建网络.对网络的统计性质,如度分布、平均路径长度、聚类系数等进行考察,发现不同动力学过程产生的序列,对应的网络拓扑结构表现出明显的差异——噪声周期信号生成随机网络;混沌时间序列生成具有小世界和无标度特性的网络.网络的统计性质可以反映和量化嵌入混沌吸引子的不稳定周期轨道的层次结构.

采用这种方法对时间序列进行分析,的确可以从宏观尺度挖掘到网络的一些信息,如度分布、平均路径长度等;但有的网络即使全局性信息相同,但仍存在显著的局部性差异,这就要求从微观尺度探测系统内部的结构特征.文献[8]研究了网络的不同子图出现的相对频率,用来刻画不同类型的连续性系统,找出隐藏在内部的信息差异,并据此为序列分类.事实证明,这种方法确实可以将混沌、超混沌和噪声等信号区分开来.

文献[9-13]从时间序列分析的相空间重构出发,把长度固定的时间序列片段映射为网络的节点,这些节点之间的关联系数作为判断这些节点之间是否连接的依据.当关联系数绝对值大于某一阈值的时候,认为两个节点连接.该文中提出了一个有效确定阈值的方法,也就是同时调相空间维数和阈值,使得在一个很宽的参数范围内,度分布服从的函数形式不变,并且拟合参数不再变化,该稳定区被认为反映了序列本身的一些固有的性质.这种方法应用于现实中的时间序列,发现能够很好地反映不同股票序列之间的差异.当然,这种方法也存在问题,要想准确地估计两个状态变量间的相关系数,通常需要足够大的嵌入维数,因此就会丢失序列上的局部信息,甚至会给系统带来伪相关.

文献[14-15]提出了一种基于流体动力学复杂网络的等价方法,并成功地应用于气液两相流中导电信号的非线性系统.文献[16]也采用相似的技术,考虑了多个序列之间的关系网络.把每个时间序列作为节点,而序列之间的关联系数作为连接与否的依据.

文献[17-18]提出了一种可见图的方法.时间序列的点映射成节点,如果两个节点之间的所有节点都落在这两个节点连线的下面,也就是两个节点“可见”,两者之间建立边连接.这种网络的优点是保持了原时间序列的大部分性质,周期序列、随机序列、分形序列分别转化为规则网络、随机网络和无标度网络.

可见图的一个重要的应用是估算分数布朗运动的休斯特指数(Hurst exponent).分数布朗运动的可见图的度分布满足幂律函数,理论推导知,幂律指数α是休斯特指数H的线性函数,α=3-2H.文献[19]考察了分数布朗运动和多重分形随机游走序列的可见图方法,独立地得出此结论.

可见图首先应用于汇率序列的分析[12].选取6个重要的汇率序列作为研究对象(CAD加元,EUR欧元,JPY日元,GBP英镑,NZD新西兰元和AUD澳元).结果表明,这些序列最后转化成了无标度和具有层次结构的网络,度分布的标度指数和H之间服从分数布朗运动的分析预测.将可见图方法与小波最大模方法算出的H结果进行对比,证明了可见图算法的可靠性.欧元和日元的汇率被广泛用来评估风险和估计风险投资中的趋势.这两种汇率序列的可见图的层次性比其它汇率序列的要弱得多,这说明可见图揭示出了汇率序列的非平凡性质.

可见图也用于心跳信号分析[20].研究发现,相应的网络都是无标度网络、具有很高的聚类系数、明显的层次结构和明显的同配混合性,尤其是可以用网络的同配系数识别充血性心力衰竭.文献[21]对此提出了质疑,指出序列长度(网络的规模)对同配混合模式的影响,认为同配系数不能作为划分健康者与病人的指标.

由于可见图构造规则的原因,可见图很难进行理论分析,为此文献[22]提出了可见图的子图——水平可见图.水平可见图的定义是在可见图基础上简化而来的.构建规则是序列数据点作为节点,如果两个节点的值大于它们之间的所有节点的值,在这两个节点之间建立一条边.该方法可以很容易地将混沌与随机序列区分开来,包括低维混沌、噪声低维混沌、高维混沌序列.与其它算法相比较,该算法的计算成本低,可以得到精确的解析解.但是,该方法是否可以量化混沌,还要考虑到表达混沌的一些通用指标(如李亚普诺夫指数、相关维数等),此问题有待于进一步深入研究.

综上所述,时间序列映射到复杂网络,采用复杂网络理论提取时间序列特征,已经开展了一些具有启发意义的方法和理论研究.对实际序列分析表明这一方向具有潜在的应用前景.但是,这些研究都是针对理论模型产生的标准序列进行的.当应用于现实序列的分析时,仍有许多基本的问题需要解决.现实时间序列是非平稳的,也不可避免地受到噪声的影响.理论上可以看作是平稳序列与趋势序列以及噪声信号的叠加.因此,必须回答的问题包括混合序列中各种成分竞争特点和复杂网络研究时间序列能够给出那些新的信息.笔者将以可见图方法为例,考虑具有不同修斯特指数的分数布朗运动的混合序列,探索这些成分之间的竞争特点.与小波分析方法比较,阐释可见图方法的优缺点,指出联合使用小波分析和可见图的必要性.进一步把可见图方法推广到二维地貌的描述,提出二维可见图(2D visibility graph)概念.在此基础上指出发展方向.

2 数布朗运动混合序列可见图

实际时间序列往往是多个时间序列的整合,如各种经济指数、股市综合指数等.如何理解这些时间序列的复杂网络性质,是一个基本的问题.为此研究了多个分数布朗运动叠加序列中多成分竞争问题[23],分析了时间序列竞争对可见图性质的影响.发现对于由两个不同指数分数布朗运动序列得到的混合序列,可见图的性质由具有较小 H指数的序列成分决定.这个结论可以推广到多成分混合序列.

首先产生两个标准化的fBm序列{y1i｜i=1,2,…,N}和{y2i｜i=1,2,…,N},对应的分形指数分别为H1和H2.一个混合序列可以表示为

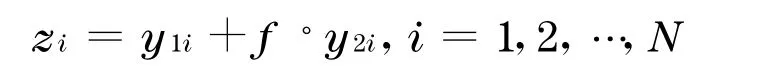
式中,f为调节序列中两个序列成分相对强度的参数.

一个多重的叠加序列可以表示为

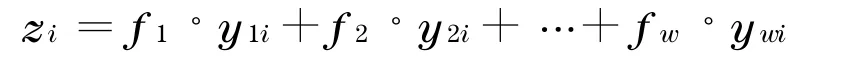
式中,w为组分的个数;

图1为两个分数布朗运动混合序列与原始序列的度分布p(k)函数与度k关系示意图.混合相对强度为1,H1和H2分别为0.2,0.5.原始序列和混合序列的可见图都为无标度网络,并且混合序列的无标度指数与H为0.2的序列的无标度指数相近.

图2为混合序列可见图度分布指数αm与混合成份的H1和H2的关系.发现混合序列的度分布都满足幂律,并且幂律指数与具有较小的H指数的分数布朗运动序列的指数相同.图3(见下页)为f对αm的影响,可以观察到大约f≥0.2的时候,较小H的序列成分在可见图中占主导地位.

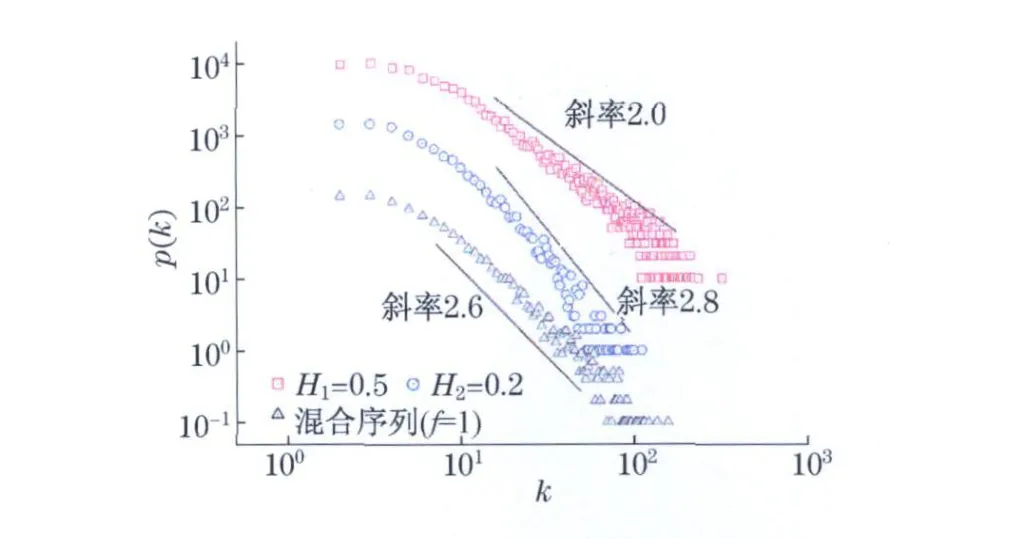
图1 混合序列可见图的p(k)与k的关系Fig.1 Degree distibution,p(k)for visibility graphs of nvxed series

图2 αm与混合成份H1和H2的关系Fig.2 Relation of αmversusH1ang H2

3 二维地貌可见图

现在的研究,主要是针对一维时间序列开展的.而实际上二维空间的数据分析,有着更加广泛的应用背景.在生物、物理、地理、大气等诸多领域,地貌(landscape)是一个重要的概念[24].如蛋白质折叠过程由二维空间上的势能曲面决定.而一个表面的粗糙度是认识力学、催化等作用的重要概念.因此,如何把复杂网络理论应用于地貌研究,有着重要的理论和应用价值.为此本文提出二维可见图(2D visibility graph)概念,作为应用的例子研究了分形表面的结构特征.

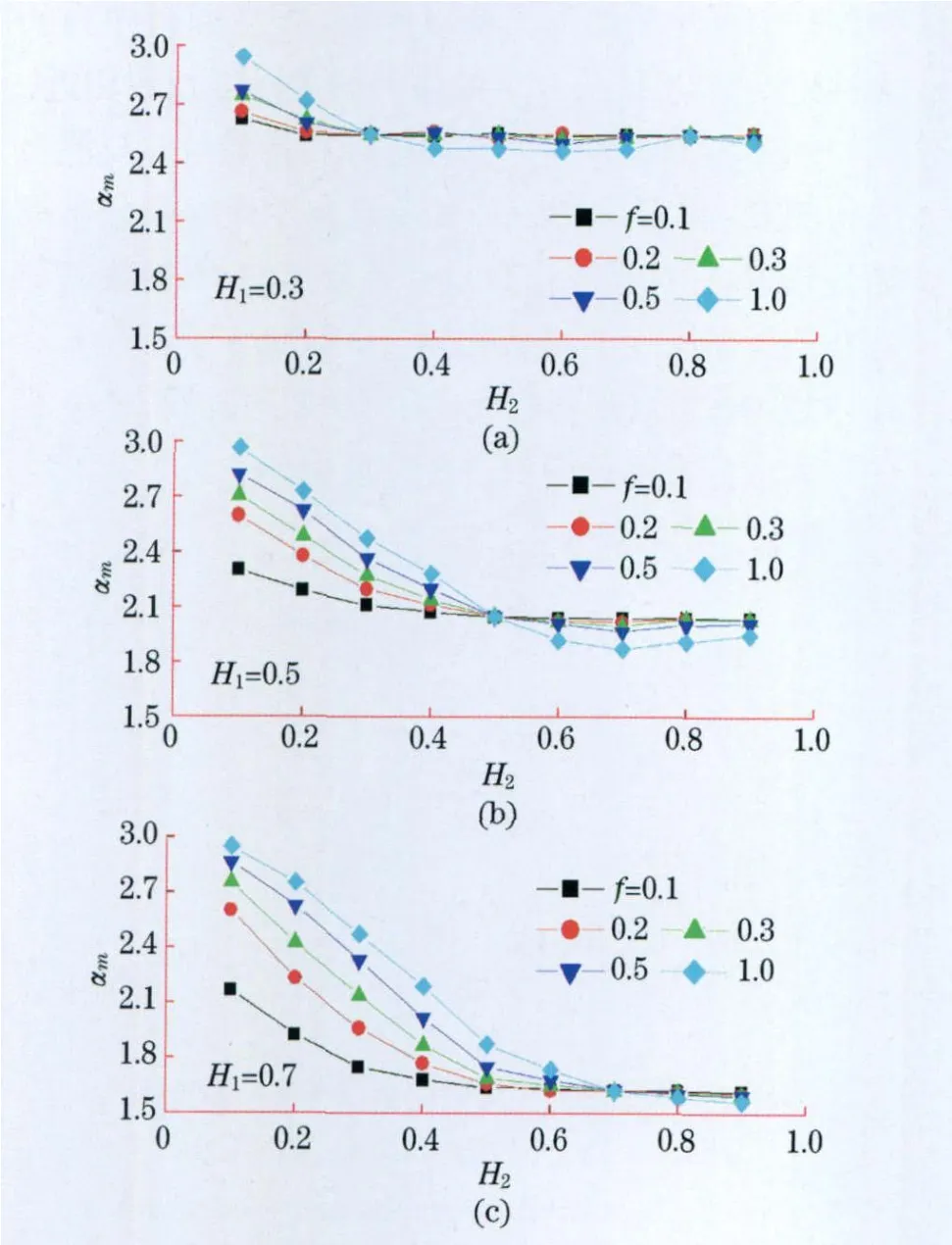
图3 f对αm的影响Fig.3 Impacf of f on αm

对于二维空间的数据,对其行、列分别应用可见图规则,构成二维可见图.二维规则分形粗糙表面可以由生成元逐次迭代生成,测度量是表面上的几何高度,即在二维表面上各点处的几何高度是按一定的生成规则分布的[25].

多分形用于二维粗糙表面的定量表征,简单分形维数仅可以对粗糙表面做整体上的表征,多重分形谱可以全面反映表面上几何高度的概率分布,但无法体现空间结构特征.利用复杂网络中度分布、群集系数、层次结构、社区结构等参量,不仅可以从统计角度对物体表面粗糙程度进行表征,还可以更清晰地反映表面的局部信息.

选择32×32和64×64尺度的生成元为P/P/ P/(1-3P)的二维规则粗糙表面.计算原始地貌和打乱顺序的地貌二维可见图的度分布见图4所示的二维可见图度分布指数α与第一生成元取值P的关系,层次结构图见图5所示的层次结构指数β与P的关系.

从图中可以看出,不同尺度下,同一类型的标度指数变化不大.原始地貌和打乱次序的地貌的可见图的节点度布服从幂律分布,并且原始地貌的幂律指数明显低于打乱顺序的地貌的幂律指数,说明二维可见图能提取到地貌结构相关的信息.从层次结构图来看,分形地貌的β更接近于1,因此其层次结构明显好于打乱顺序之后的网络.

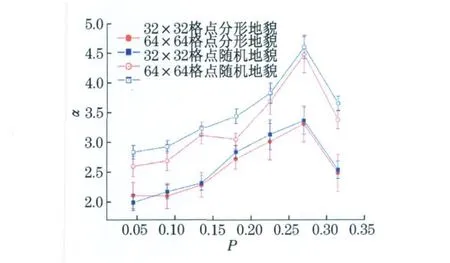
图4 α与P的关系Fig.4 Relation ofα versus p

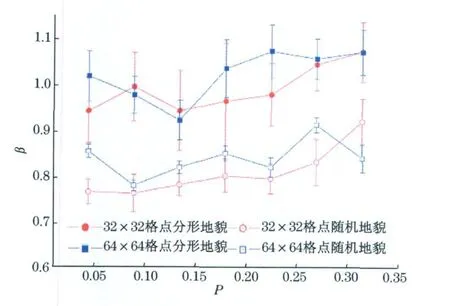
图5 β与P的关系Fig.5 Relation of β versus p

4 联合使用小波分析和可见图

作为一种新的时间序列分析工具,时间序列的复杂网络理论能否给出一些新的,其它方法不能揭示的时间序列特征和隐含的动力学性质,这是必须要回答的问题.

关于这一问题,本文比较了分数布朗运动的线性叠加序列和多分形序列的可见图的性质.发现对于这两种不同的时间序列,小波方法发现都具有多分形性质,不能有效识别之间的差异;而可见图的度分布,对于线性叠加序列小的 H成份占优势,仍呈现为无标度特征;多分形序列的可见图的度分布失去了无标度特征.因此,结合小波分析和可见图方法,才能更好地区分这两种时间序列.

考虑两个有不同的H值的单分形序列叠加后的竞争行为.图6为线性叠加分数布朗运动的多份形谱D(h)与分形维数h的关系,图6中给出了H分别为0.5和0.8的两个序列叠加(权重因子为1)得到的混合序列的多分形谱.这一叠加序列是一个多重分形序列,其分形强度Δ h=0.39.也就是说两个单分形序列叠加的序列已经不是单分形的序列了,而是具有一定分形强度的多重分形序列.H值为0.54.也就是混合序列的H更接近于H为0.5的序列成分.这也进一步验证了具有较小H值的成分主导混合序列性质的结论.

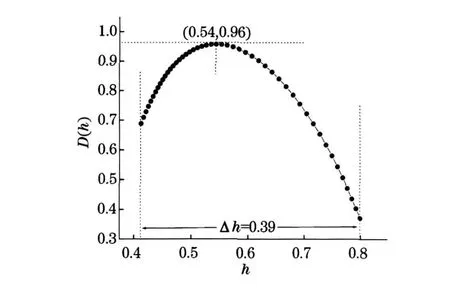
图6 D(h)与h的关系Fig.6 Multl-frolfal spectram,D(h)

现考虑二进制模型产生的多重分形时间序列xk=an(k-1)(1-a)nmax-n(k-1),k=1,2,…,N.其中0. 5＜a＜1,序列长度为N=2nmax,参数n(k)为把十进制数k转换成二进制并计算出其中1的个数,例如n(13)=3.

上述二进制模型给出的时间序列是多重分形序列.以a=0.75,序列长度为65 536为例,由图7所示的二进制模型产生的多分型序列可见图的p(k)与k关系可见,p(k)在双对数坐标下呈非线性.调整参数a从0.5到1,以0.05为间隔,得到的结果都呈现非幂率分布.

因此,小波分析不能区分单分形叠加得到的混合序列和模型产生的多分形序列.这是一个值得注意的问题,因为文献中经常采用多分形模型去模拟和再现现实中的具有多分形特征的时间序列.可见图能够区分这两种多分形序列,但是不能区分单分形和混合序列.因此联合运用小波分析和可见图分析才能较好地识别这两种完全不同性质的序列,给出可靠的关于序列形成机制的结论.

图7 多分形序列可见图p(k)与k关系Fig.7 Degree distibution p(k)for visibilify graphs of multi-fractal series

5 总 结

采用复杂网络理论分析时间序列,处于刚刚起步阶段.发展有效的时间序列映射到网络的方法是关键.从理论走向应用必须解决一系列的问题,这是进一步发展的方向.一个普遍存在的问题是噪声问题.复杂系统不可避免地会受到外界的噪声的影响;同时现实的时间序列都是有限长度的,基于有限个长度的时间序列的关联分析,会带来统计上的涨落.因此,噪声对结果的影响是必须解决的问题之一.

另一个是趋势的影响.时间序列一般来讲存在着宏观意义上的趋势,如人口数量在涨落的同时持续的增加、股票价格的总体上涨等.这些趋向的存在,是以统计理论为基础的序列关联所不允许的.在时间序列分析中,消除趋向带来的伪结果,一直是研究的核心内容之一.因此,时间序列的趋向对结果的影响以及如何消除这一影响是必须解决的问题之二.

第三个,也是核心的问题,发展起来的方法能否给出新的,其它方法不能给出的性质.这也是诸多方法的缺陷所在.

[1] MANTEGNA R N,STABLEY H E.Introduction to Economic Physics:Correlations&Complexity in Finance [M].Cambridge:Cambridge University Press,2000.

[2] SM ALL M.Applied Nonlinear Time Series Analysis: Applications in Physics[M].Singapore:World Scientific,2005.

[3] STANEY H E,PLEROU V,GABAIX X.A statistical physics view of financial fluctuations:Evidence for scaling and universality[J].Physica A,2008, 387:3967-3981.

[4] ALBERT R,BARABASI A L.Statistical mechanics of complex networks[J].Rev Mod Phys,2002,74: 47-97.

[5] ALON U.An Introduction to Systems Biology:Design Principles of Biological Circuits[M].Pennsylvania:Chapman&Hall/CRC,2006.

[6] ZHANG J,SAM LL M.Complex network from pseudoperiodic time series:Topology versus dynamics [J].Phys Rev Lett,2006,96:238701.

[7] ZHANG J,LUO X,NAKAMURA T,et al.Detecting temporal and spatial correlations in pseudo-periodic time series[J].Phys Rev E,2007,75:016218.

[8] XU X,ZHANG J,SMA LL M.Super-family phenomena and motif of networks induced from time series[J].Proc Natl Acad Sci,2008,105:19601 -19605.

[9] YANG Y,YANG H.Complex network-based time series analysis[J].PhysicaA,2008,387:1381 -1386.

[10] JIANG Z,YANG H,WANG J.Complexities of human promoter sequences[J].Physica A,2009,388: 1299-1302.

[11] WANG J,YANG H.Complex network-based analysis of air temperature data in China[J].M od Phys Lett B,2009,23:1781-1789.

[12] YANG Y,WANG J,YANG H,et al.Visibility graph approach to exchange rate series[J].Physica A,2009,388:4431-4437.

[13] DONNER R V,ZOU Y.Recurrence networks—a novel paradigm for nonlinear time series analysis[J]. New J Phys,2010,12:033025.

[14] GAO Z,JIN N.Flow-pattern identification and nonlinear dynamics of gas-liquid two-phase flow in complex networks [J].Phys Rev E,2009, 79:066303.

[15] GAO Z,JIN N.Community structure detection in complex networks with applicationstogas-liquid two-phase flow[J].LNICST,2009,5:1917-1928.

[16] LUO F.Constructing gene co-expression networks and predicting functions of unknown genes by random matrix theory[J].BMC Bioinformatics,2007,8:299.

[17] LACASA L,LUQUE B,LUQUE J,et al.From time series to complex networks:The visibility graph [J].Proc Natl Acad Sci,2008,105:4972-4975.

[18] LACASA L,LUQUE B,LUQUE J,et al.The visibility graph:A new method for estimatingthe hurst exponent of fractional Brownian motion[J].Europhys Lett,2009,86:30001.

[19] NI X,JIANG Z,ZHOU W.Degree distributions of the visibility graphs mapped from fractional Brownian motions and multi-fractal random walks[J].Phys Lett A,2009,373:3822-3826.

[20] SHAO Z.Network analysis of human heartbeat dynamics[J].Appl Phys Lett,2010,96:073703.

[21] ZHAO D,LI X.Comment on“Network analysis of human heartbeat dynamics”[J].Appl Phys Lett, 2010,96:266101.

[22] LUQUE B,LACASA L,BALLESTEROS F,et al. Horizontal visibility graphs:Exact results for random time series[J].Phys Rev E,2009,80:046103.

[23] 王建波.基于复杂网络理论的时间序列分析[D].上海:上海理工大学,2010.

[24] BAI Y.Protein Folding Protocols[M].New Jersey: Human Press,2008.

[25] 孙霞,吴自勤,黄畇.分形原理及其应用[M].合肥:中国科学技术大学出版社,2003:60-67.