浅议全站仪悬高测量的难点及改进方法

陈昌耀

(紫金矿业集团股份有限公司，福建上杭 364200)

1 前言

对于架空的线路或构筑物(如高耸的烟囱或者大型储料罐等)，当要求精确测量其悬高时，由于不能(或不方便)在悬高物体处设置反光棱镜，即使具有免棱镜功能的全站仪，其免棱镜测距的测程有时无法到达欲测的目标，这时一般采用间接测量的方法，通过间接测量方法得到悬高。这种方法，首先应设法测定架空目标在地面的铅垂投影点的点位，再由测站点观测目标及其投影点的垂直角，利用三角函数关系解算目标的悬高。通常情况下，一般全站仪均内置有悬高测量程序，可易测出悬高物体的悬高。但是，要确定架空目标在地面的铅垂投影点的点位显然并不容易。本文对悬高测量的做法和计算进行改进，可测出较为准确的悬高。

2 全站仪悬高测量的基本原理

在距离悬高物体不远的，地形起伏较小合适位置，进行设站，同时在悬高物体铅垂投影点的点位上置棱镜，可以利用全站仪内置悬高测量程序方便测出悬高物体的悬高。计算公式如下:

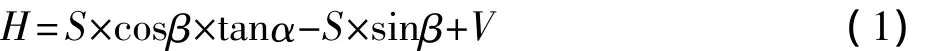
式中:H为悬高物体的悬高;S为全站仪至反射棱镜的斜距;α为目标点的竖直角;β为反射棱镜的竖直角;V为反射棱镜高。如图1所示。

图1 全站仪悬高测量示意图

从原理上看，利用全站仪可以很容易测出悬高物体的悬高，但是这是建立在已经确定置棱镜的地面点就是悬高目标的铅垂点。而实际上要准确确定这个铅垂点是非常困难的，主要是依靠人工目测确定。同时有些悬高物体的铅垂点无法置棱镜，比如高炉、烟囱、高架塔等。那么如何确定呢?根据文献［1］提供的两次设站可以较为精确测出所测的目标悬高的思路，可以采用两次设站方式进行确定。

3 解决方法

主要采用两次设站的方法，两次设站均要求和悬高物体，置棱镜点，观测仪器点在同一铅垂面上。

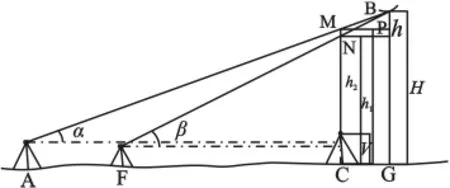
图2 两次设站测悬高示意图(一)

图3 两次设站测悬高示意图(二)

(1)将全站仪置于观测位置较好的地点A(见图2或者图3)，整平。同时将棱镜置于悬高物体B点下的C点，尽可能接近悬高物体的铅垂线，即尽量接近BG线。棱镜面对全站仪。

(2)调用全站仪悬高测量程序，输入棱镜高，对准棱镜进行测量，而后旋转望远镜照准悬高物体目标点，必须保证全站仪水平角不动。可以测出此时悬高物体的悬高h1。注意，该悬高不是真正的悬高物体的悬高h1。而是点M与点C之间的高度

(3)记录好全站仪此时的悬高和垂直角α(或天顶距)，然后利用全站仪水平角不动，旋转望远镜实地测出新的设站点F，注意新的设站点F必须在原设站点与置棱镜点的连线上。

(4)将全站仪置于新的设站点F，重复操作步骤(2)，注意要求置棱镜点在步骤(1)中是同一点，得出新的悬高物体的悬高h2。并记录好新的设站点的观测的悬高h2和垂直角β(或天顶距)。

(5)根据两次观测出的悬高和垂直角，通过三角形函数和定理关系计算出较为准确的悬高H。

因目测悬高物体点误差，造成形成如图2和如图3问题。为方便公式推导，因置棱镜点C与点G之间的高程忽略不计。

以图2为例，公式推导如下:根据图2可以看到，分别过M和N做水平线有，两次测出的悬高差h=h1－h2;

为点M与点N之间的高差。在三角形△MNB中，可以根据正弦定理:

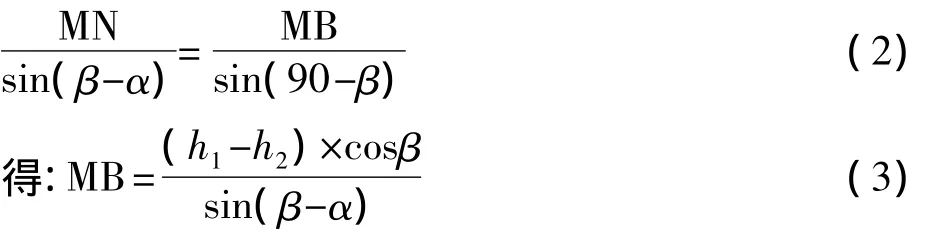
欲求的悬高H，则要利用h1和BP之和。在三角形△MBP中，由直角三角形的正弦函数，有:

将式(3)代入式(4)有:

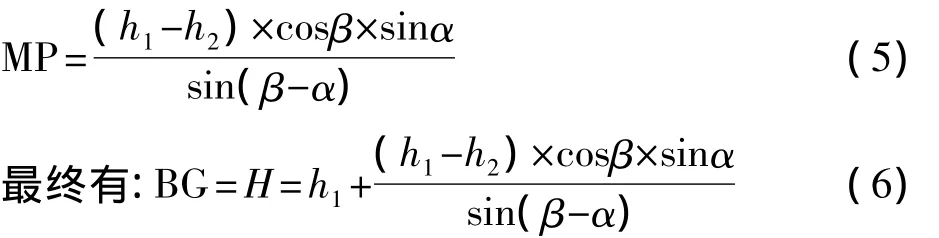
以上是根据图2推导出的公式，图3中的公式也是一样可以推导式(6)。由于式(6)简单明了，可以利用可编程计算器很快计算出最终悬高。

同时因全站仪可以直接测距，可以通过计算出的悬高H计算出FG平距，与实际测出的FC平距的差值。若点C与点G之间可以移动，则移动棱镜至点G，再次测出悬高，比较此时测出的悬高和计算出的悬高H，以便校核。

4 实例

选择一个不算太高的悬空物，没有选择较高的悬空物，主要是想用免棱镜全站仪校核数据。按照前操作步骤，测得h1=14.82 m，h2=14.80 m，α=8°02′21″，β=9°00'02″。根据式(6)可以计算出:

实际采用免棱镜测量时测得高差为15.01 m。考虑到实际测量的误差和立棱镜点与实际铅垂点之间误差，可以说误差相当小。

5 结论和注意事项

虽然通过此方法可以得出悬高物体的悬高，但是仍需注意以下几项方可取得较为精确的悬高置。

(1)尽可能选择设站点与悬高目标之间的垂直角不要太大和太小，太大和太小均不易精确瞄准悬高物体同一点。

(2)观测位置和置棱镜位置地势尽可能比较平缓，这样可以减少三角高程测量带来的误差影响。

(3)置棱镜点尽量逼近悬高物体的铅垂点，以便减小因置棱镜点与铅垂点之间的高差影响。

通过以上方法，我们知道可以较为准确的测出悬高物体的悬高。而操作是比较方便的。但是此方法是建立在设站点和置棱镜点及悬高物体点都是在一截面上而成的。对于不是同一截面，则不能利用这个方法。

［1］ 何国祥.对精确悬高测量方法的再探讨［J］.测绘通报，2006(6)

［2］ 张国良.矿山测量学［M］.徐州:中国矿业大学出版社，2001

［3］ 张正禄.工程测量学［M］.武汉:武汉大学出版社，2002

［4］ 王俊江.精确悬高测量方法的讨论［J］.新疆有色金属，2007(2)

［5］ 陆国胜，王学颖编著.测量学基础［M］.北京:测绘出版社，2006