基于Duffing振子的DSSS信号率线检测
2011-03-21金虎
金 虎
(解放军电子工程学院,合肥 230037)
1 引 言
直接序列扩频(简称DS)信号率线检测法是通过对DS信号进行非线性变换,使其在码元速率处出现一线谱分量(即率线),检测该线谱分量可以确定信号存在与否的一种扩频信号检测方法[1-3]。通常用非线性变换后的信号与不同频率的复正弦波相关,即离散傅里叶变换(DFT)来检测。检测的依据是信号在率线频率fb及(或)它的倍频kfb处是否存在离散的谱线,如果输出信号在 fb及(或)kfb频率处的幅度明显高于其邻域的幅度,则说明输出信号存在谱线,从而推断信号存在。当输入信噪比较低时,性能急剧下降,要以增加采样数据为代价。
实际上,频域内检测大小为码元速率的线谱是否存在反映到时域内就是检测频率大小为码元速率的正弦信号是否存在。本文根据混沌微弱信号检测理论,利用Duffing振子对周期小信号具有敏感性同时对噪声具有免疫力的特性来检测DSSS信号率线检测方法中非线性变换后的正弦信号。
2 基于Duffing振子的率线检测法
2.1 率线检测基本原理
率线检测中非线性变换通常是将信号预滤波,然后与其延迟相乘,即滤波-延时-相乘检测器(Prefilter-Delay-And-Multiply,PFDM)。率线检测器用于在fb=1/Tc及其谐波处产生线谱分量,要求在fb处产生的线谱分量最大,而其谐波处的谱分量尽可能地小。同时,为了便于区分线谱分量,要求在该线谱分量附近的其它谱分量也较小。
当信号的基带脉冲是矩形时,在高斯白噪声下,最优率线检测器输出端的归一化谱信噪比最大值为[1]

式中,a为二元随机变量的幅度,Tc是一个chip持续时间,E0/N0=a2Tc/N0为系统的输入信噪比。由式(1)可以看出,率线谱信噪比以k2的速度减小,所以检测率线时,只需检测率线基波线谱就可以了。
由于发送端所使用的滤波器以及码元速率未知,只能使用非最优的结构。一般的做法是令接收滤波器为频域矩形窗,即

率线基波分量谱信噪比为

改变带宽B、时延τ和率线频率fb,可以得到上述率线检测器对这些参数的稳健性。分析表明,当τ=1/B时,率线检测器对fb有很好的稳健性,在0.6B~1.4B范围内都有很好的检测性能。
2.2 基于Duffing振子的率线检测器
适合正弦信号的混沌检测模型为改进的Holmes型Duffing振子[4-5],其动力学方程为

式中,k为阻尼比;-x3+x5为非线性恢复力;γ cos(ω t)为周期策动力(参考信号),当 γ大于某一阈值γd,振子由混沌态进入大尺度周期态;fcos(ω t)+n(t)表示混有噪声的待测信号,f为待测信号幅值,n(t)为噪声。一般地,要求 γ远大于f,噪声的均值为零[6,7]。改变方程中的 ω值就可以适应不同的待测信号频率。
基于Duffing振子的DS信号率线检测原理框图如图1所示。带通滤波器输出信号与自身延迟相乘后的信号通过去直流(均值为零)后,作为Duffing振子的周期摄动力加入到Duffing振子中。通过Duffing振子的相态是否改变来达到检测DSSS信号的目的。
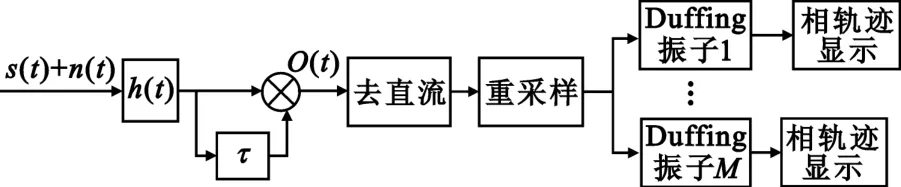
图1 基于Duffing振子的DSSS/BPSK信号率线检测框图Fig.1 The block diagram of DSSS/BPSK rate-line detection based on Duffing oscillator
设待测信号是DSSS/BPSK信号,其时域表达式为
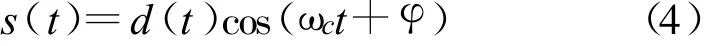
式中,d(t)是基带扩频信号,ωc是载频角频率,φ是载波相位。则其延迟相乘的输出为
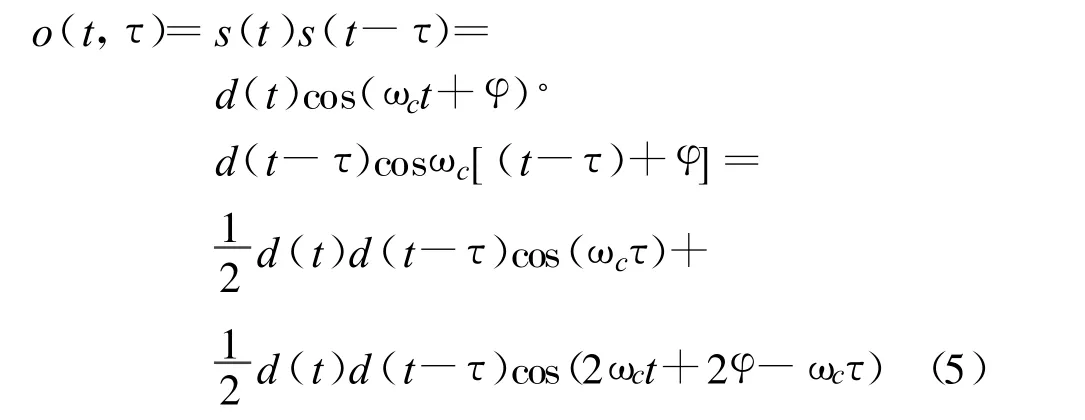
式中,第一项包含有率线基波 fb,其幅值大小为,受乘积因子 cos(ωcτ)的影响,在载频固定的情况下,幅值随延迟 τ呈正弦变化,使得幅值有可能为零,所以检测该项中的率线基波并不可靠;第二项单独写为(忽略系数1/2)

式中,z(t)表示所有其它信号及噪声;

从式(6)可以看出,延迟相乘后产生频率为2fc±fb的周期信号,这就是我们要检测的线谱。下面以检测2fc+fb的线谱为例进行分析仿真。
将式(3)中周期策动力的 ω设为2fc+fb,并调整Duffing振子的 γ值,使得Duffing振子处于临界混沌态,即使得 γ值略小于 γd。将 o(t,τ)去直流后的信号作为周期摄动力加入到Duffing振子中,代替式(3)中的 fcos(ω t)+n(t)。不失一般性,就以作为周期策动力和待测信号的相位差,从式(7)可以看出,这里相差不仅与载波相位有关,还与时延 τ有关。根据Duffing振子特性,可得振子进入大尺度周期态时相位差 的取值范围为[8]


在码率未知的情况下,要检测2fc+fb的线谱是否存在,就要对混沌测检系统的 ω在2π·[2fc+(0.6B~1.4B)]的范围内取不同的值进行搜索检测,或用一组不同 ω值的Duffing振子去覆盖感兴趣的频段。此时若设置参考信号的频率与待测信号的频率一致,理论上需要无穷个Duffing振子来覆盖感兴趣的频段;若采用一个Duffing振子,则 ω要改变无穷次,这在实际中是不可能实现的。
此时,我们可以利用Duffing振子的有规律间歇混沌现象来估计信号频率,这是Duffing振子参考信号频率与加入到Duffing振子的待测周期信号频率存在一定的偏差(设为Δω)而产生的一种现象,间歇混沌现象的循环周期为ΔT=2π/Δω。仿真和实验表明[9],当 Δω/ω ≥0.04时,有规则的间歇混沌被破坏。所以我们在用一组Duffing振子来检测周期信号时,要根据这个要求来设置每个Duffing振子的 ω值。
若Duffing振子的频率限制在1~10的范围内,一组振子的频率表示为 ω1,ω2,…,ωi,…,ωM,设各频率点成等比数列,公比为1.03[10],即:

式中,M=79。采用间歇混沌现象检测信号要求间歇混沌现象只能发生在相邻的两个Duffing振子上而其它的振子仍处于混沌态。如果公比小于1.03,有可能导致两个以上的振子进入间歇混沌态;如果公比大于1.03,间歇混沌现象有可能只会出现在一个振子上,且可能无规则。所以1.03是最合适的公比,从而得到Duffing振子的数目为79。
如果周期信号的频率不在1~10的范围之内,在检测前就要做一些预处理工作。假设以采样率v对信号进行采样,然后以采样率10nv(n=…-3,-2,-1,0,1,2,3,…)对采样数列重采样,这样只需调整n的值就可以使重采样信号的频率在1~10之间。但是在实际测量中,覆盖的频率范围可能比较广,即使进行预处理,也不能把频率范围完全控制在1~10之内,有两种解决方法。
(1)不进行预处理,在频率覆盖的范围内按照公比1.03分成若干个频率点,每个频率点用一个Duffnig振子去检测。这样的话,存在4个不好的方面:一是待测频率比较高时,每个Duffing振子的工作频率就比较高,会降低运行速度;二是需要的Duffing振子数目可能比较多;三是对于不同的频率范围Duffing振子的频率和数目都是变化的,不利于硬件或软件实现;四是估计精度会比较低。
(2)将工作的频率范围分成若干个小的范围,每个小范围通过处理都可以变化到1~10内,再用固定的含有79个Duffing振子的振子阵列对每个小频率范围进行检测,或者采用多个Duffing振子阵列对若干个小范围同时检测。这种方法的好处是:所用的Duffing振子的频率和数目是固定的,便于硬件或软件实现。
3 仿真及性能分析
为了减少仿真数据量,仿真时随机序列a(t)取码长为511的PN码,码率 Rc=4 bit/s,采样率 fs=1000 sample/s,载波角频率 ωc=16πrad/s,滤波器带宽 B=15 Hz,时延 τ=1/B=1/15 s。式(3)中,ω=2ωc+fb=40πrad/s,k=0.5,用 4阶 Runge-Kutta解微分方程,步长h=0.001(与采样间隔相等),应用双精度运算可得 γd=0.7332691,所以取 γ=0.7332690使Duffing振子处于临界混沌状态。若=0 rad时,仿真可得当率线检测器输入端信噪比SNR=-29.01dB时Duffing振子进入大尺度周期态。
图2显示的是Duffig振子输入端信号的时域波形和幅度谱,其中时域波形图中的白色部分是DSSS/BPSK信号,可见信号是淹没在强背景噪声中的。图3显示的是Duffing振子输出信号的时域波形和幅度谱。从图3中可以看出,频率为20 Hz的率线很好地从噪声中提取出来了。
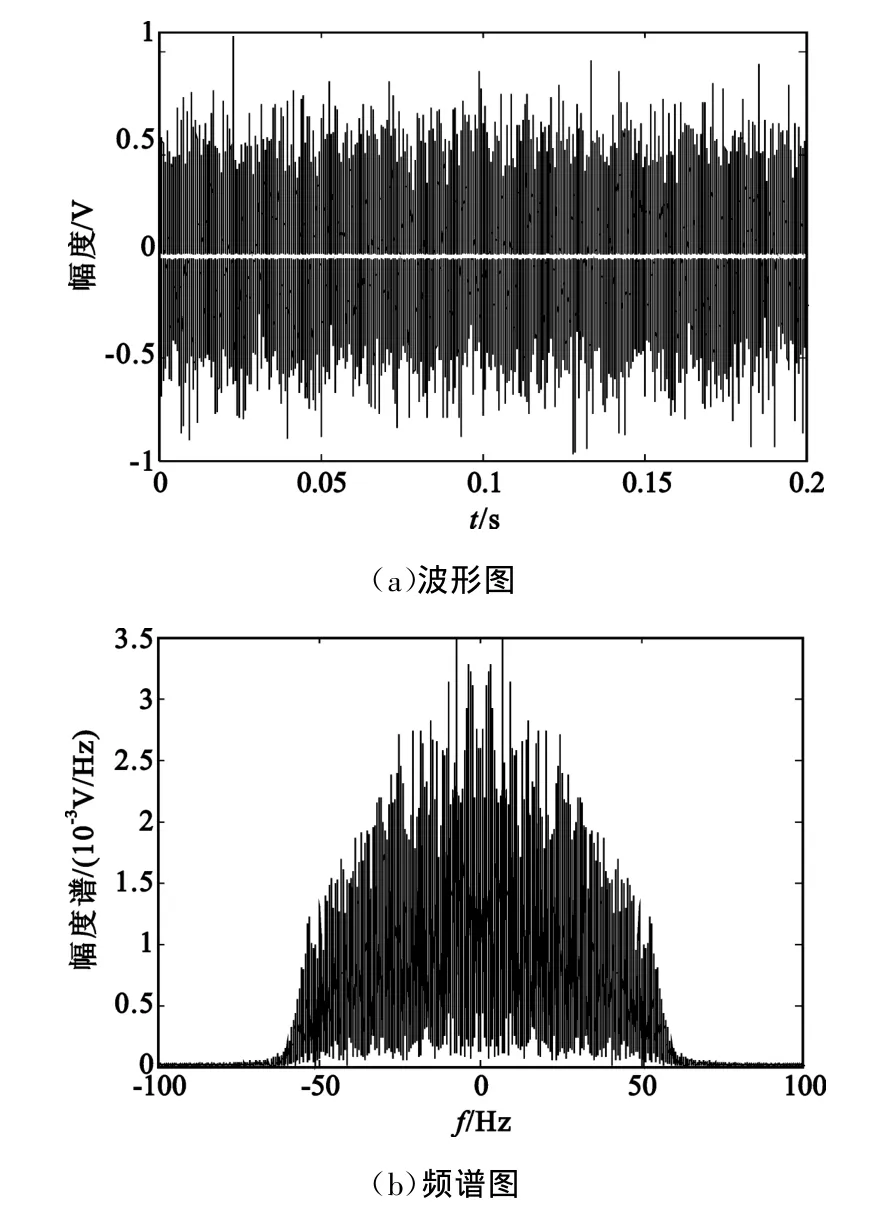
图2 率线检测器输入信号的波形和频谱图(SNR=-29.01dB)Fig.2 Wave and spectrum of the input of the rate-line detector(SNR=-29.01dB)

图3 基于Duffing振子的率线检波器输出信号的波形和频谱图(SNR=-29.01dB)Fig.3 Wave and spectrum of the output of the rate-line detector based on Duffing oscillator(SNR=-29.01dB)
表1显示的是不同相位差时可检测到DSSS/BPSK信号的最低信噪比,图4是其相应的关系曲线。从最小二乘的意义上获得该曲线的拟合方程为

式中,rSNR()表示不同 时最低可检测信噪比。拟合方程的误差为-2.288~2.345dB,拟合方程曲线如图4中虚线所示。从图中可看出,率线检测器最低可检测信噪比在整个可允许的相差范围内受相差的影响比较大,尤其当相差达到±5π/12时,检测性能就变得非常差了,为-5.95dB,此时,一般不能满足DSSS信号的检测要求了。

表1 在不同相位差下可检测到DSSS/BPSK信号时的最小信噪比Table 1 Minimum SNR of detectable DSSS/BPSK signal with different phase difference

图4 相位差与可检测DSSS/BPSK信号时最小信噪比关系曲线Fig.4 Relative curve between minimum SNR of detectable DSSS/BPSK signal and phase difference
4 小 结
充分利用Duffing振子对小信号的敏感性和对噪声的免疫性,把混沌微弱信号检测技术用于DSSS信号率线检测法中非线性变换后的正弦信号的检测。一般的噪声抑制技术检测DSSS信号最好的结果只能达到-18dB左右[11],仿真表明文中所提的检测方法有10dB的性能提高,更有利于强噪声背景下的DSSS信号的检测。
[1] Kuehls J F,Geraniotis E.Presence detection of binary phase shift keyed and direct sequence spread spectrum signals using a prefilter delay and multiply device[J].IEEE Journal on Selected Areas in Communications,1990,8(5):915-933.
[2] Wickert M A,Turcotte R L.Rate-line detection using higher-order spectra[C]//Proceedings of Military Communications Conference on Fusing Command,Control and Intelligence.San Diego,CA,USA:IEEE,1992:1221-1225.
[3] Truong T,Wickert M A.Performance of spectral line detection using integrated trispectrum[C]//Proceedings of Military Communications Conference.Boston,MA,USA:IEEE,1998:659-663.
[4] 李月,杨宝俊,石要武.色噪声背景下微弱正弦信号的混沌检测[J].物理学报,2003,52(3):526-530.LI Yue,YANG Bao-jun,SHI Yao-wu.Chaos-Based Weak Sine Wave Signal Detection Approach under Color Noise Background[J].Journal of Physics,2003,52(3):526-530.(in Chinese)
[5] 李月,杨宝俊.混沌振子检测引论[M].北京:电子工业出版社,2004:51-55.LI Yue,YANG Bao-jun.Introduction of Choas Oscillator Detection[M].Beijing:Publishing House of Electronic Industry,2004:51-55.(in Chinese)
[6] 王冠宇,陶国良,陈行,等.混沌振子在强噪声背景信号检测中的应用[J].仪器仪表学报,1997,18(2):209-212.WANG Guan-yu,TAO Guo-liang,CHEN Xing,et al.Application of Chaos Oscillator to Signal Detection under Strong Noise Background[J].Chinese Journal of Scientific Instrument,1997,18(2):209-212.(in Chinese)
[7] 李月,石要武,马海涛,等.淹没在色噪声背景下微弱方波信号的混沌检测方法[J].电子学报,2004,32(1):87-90.LI Yue,SHI Yao-wu,MA Hai-tao,et al.Chaotic Detection Method for Weak Square Wave Signal Submerged in Colored Noise[J].Acta Electronica Sinica,2004,32(1):87-90.(in Chinese)
[8] 金虎,王可人.基于Duffing振子的直接序列扩频信号检测及参数估计[J].系统工程与电子技术,2007,29(11):1823-1826.JIN Hu,WANG Ke-ren.Detection and parameters estimation of Direct Sequence Spread Spectrum Signals Based on Duffing Oscillator[J].Systems Engineering and Electronics,2007,29(11):1823-1826.(in Chinese)
[9] 张淑清,姜万录.小信号检测中间歇混沌运动的机理[J].传感技术学报,1998,23(4):37-41.ZHANG Shu-qing,JIANG Wan-lu.Intermittent Chaos Motion Mechanism in Small Signal Detection[J].Chinese Journal of Sensors and Actuators,1998,23(4):37-41.(inChinese)
[10] Guanyu Wang,DajunChen,Jianyu Lin,et al:The Application of Chaotic Oscillators to Weak Signal Detection[J].IEEE Transactions on Idustrial Electronics,1999,46(2):440-444.
[11] 冯富强,陈鹏举,武传华,等.低信噪比条件下D S信号的检测和参数估计[J].通信学报,2002,23(9):63-68.FENG Fu-qiang,CHEN Peng-ju,WU Chuan-hua,et al.The detection and parameter estimation of DS ignal in the lower SNR condition[J].Journal of China Institute of Communications,2002,23(9):63-68.(in Chinese)
