基于数控电感的PWM整流器网侧电流改善研究*

张岭，赵锦成，邵天章，马瑞平（军械工程学院电气工程系，河北石家庄050003）

随着对用电设备的谐波标准越来越严格，PWM整流器的应用日益广泛。在PWM整流器的控制中，目前研究最多、应用最广且性能较为优良的方法是在d-q同步旋转坐标系下的直接电流控制。为了实现电流的无静差调节，该方法采用坐标变换将三相交流量变换成旋转坐标系中的直流量进行控制，PI调节器积分环节的直流增益为无穷大，因此电流控制的稳态误差为零。在控制结构上，通常采用双闭环控制，即电压外环和电流内环控制。其中电压外环用于控制整流器的输出电压，电流内环实现网侧电流的波形和相位控制。

在通常的同步旋转坐标系的PI控制中，仅保证了期望的稳态性能，但不能保证在动态过程中电流的快速跟踪，因此提出了大量改进控制方案。参考文献[1]通过对影响电流动态响应速度因素进行分析，提出了利用动态过程中的无功电流来提高有功电流动态响应速度的方法。

本文对PWM整流器在d-q同步坐标系的数学模型及控制方法进行研究的基础上，基于PSCAD软件建立了其仿真模型，通过对交流侧电感的设计进行分析，提出利用数字电感器取代传统的电感线圈，使得电感参数在运行过程中可调，从而既可以实现电流的快速跟踪，又可以达到抑制谐波电流的目的。

1 PWM整流器在d-q坐标系的数学模型及控制方法

三相电压型PWM整流器的拓扑结构如图1所示。主电路采用IGBT与二极管反并联方式，Ls和Rs为电感的等效参数，C为直流滤波电容，RL为直流侧负载，uca、ucb、ucc为整流桥三相控制电压。通过坐标变换在同步旋转坐标系下PWM整流器的方程为[1-2]：

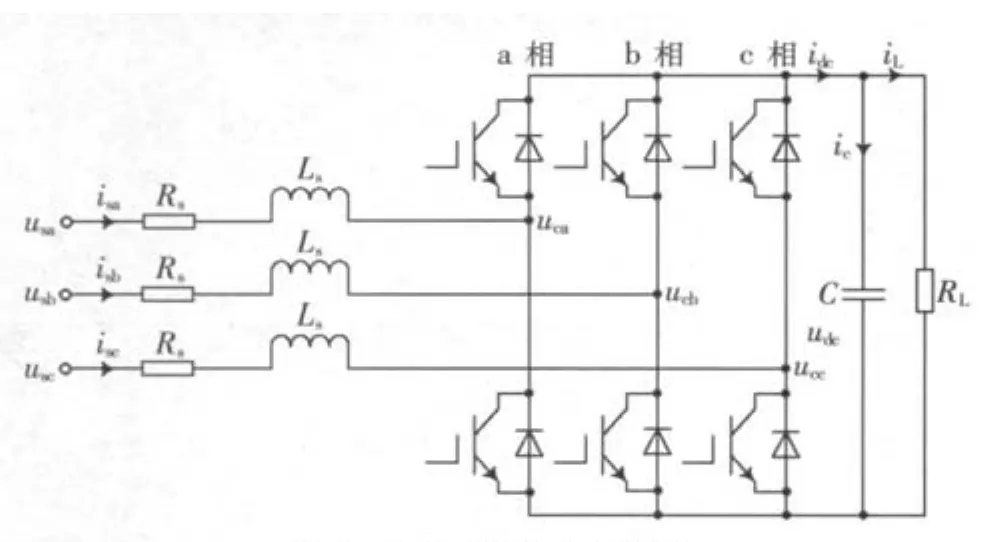
图1 电压型PWM主电路

式中，usl、isl、ucl(l=d，q)分别为d-q同步旋转坐标系下的电源电压、输入电流、桥中点控制电压。

若电源usa，usb，usc为三相对称电压，则在d-q同步旋转坐标系下的电压、电流均为直流量。通常将d轴定向于电网电压矢量同方向上，若三相对称电源相电压的最大值为Um，则：

将式(2)代入式(1)，在d-q坐标系下桥中点的控制电压为：

由式(3)、(4)可以看出，在d-q同步坐标系下，两相电流之间存在耦合，一相电流的变化将引起另一相电流的变化，因此一般的PI调节器很难达到理想的控制。

为提高电流控制的性能，使d、q轴电压ucd、ucq直接控制相应的电流isd、isq。从式(3)、式(4)可以看出，可采用检测到的实际电流补偿两相之间的耦合，以消除电流之间的相互影响，实现电流之间的解耦控制。

通过以上分析，并结合式(3)、式(4)，设计电流控制器的方程如下：

有功电流指令值i*sd与负载电流成正比，为电压调节器的输出。

当PWM整流器运行于单位功率因数整流状态时，无功功率为零，此时无功电流指令值i*sq应满足：

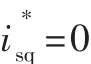
综上理论分析，利用Mannitoba HVDC研究中心的PSCAD/EMTDC工具，可以建立采用电压外环和电流内环的双闭环控制结构的PWM整流器仿真模型。

2 数字电感器原理及仿真实现

在电压型三相桥式PWM整流器中，交流侧电感的设计既要实现快速电流跟踪的指标，又要抑制谐波电流。以正弦波控制为例，当电流过零时，其电流变化率最大，为满足快速跟踪电流要求，此时电感应该足够小；而在正弦波电流峰值处，谐波电流脉动最严重，为满足抑制谐波电流的要求，此时电感应该足够大。随着新型数字化元器件的出现，使得电感的在线调整成为现实。

2.1 数字电感器原理

以往电感参数的确定是在满足有功、无功要求和电流波形品质指标的前提下，综合考虑电感的成本和体积，在满足性能要求的同时，使其数值尽量的小[3]。数字化元件采用带总线接口进行数控方式调节，可通过单片机或逻辑电路进行编程，实现了“把模拟器件放到总线上”的全新设计理念[4]。

目前MAXIM公司生产的MAX1474(6.4 pF～13.3 pF，增量0.22 pF)和Intersil公司生产的X90100(7.5 pF～14.5 pF，增量0.23 pF)两款数字电容器，可以在5 μs内快速调整。在低频情况下，可以使用高增益集成运算放大器来组成回转器，实现从电容到电感的映射，制作数字化模拟电感。

2.2 数字电感仿真设计

仿真实例取三相电压型PWM整流器，其功率为10 kW，三相交流输入电压的相电压有效值为230 V，主功率开关器件采用IGBT来实现。假设整流器效率为90%，由此可得输入功率：

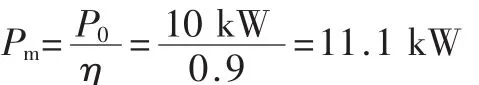
每相输入电流有效值为：

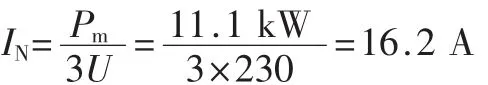
则网侧电流峰值为：

取设计值为25 A，选择功率管额定电流时，要充分考虑输入电流中含有的谐波成分。考虑2倍以上的安全系数，可选额定电流为60 A的功率管。

输出直流电压Udc应该大于三相线电压峰值，即为：

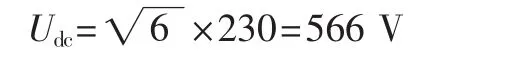
Udc取600 V，工作频率为20 kHz，最大电流imax按选择功率管的设计值选取，Δimax为电流波动的最大峰值，通常情况取Δimax=20%×imax。则电感值的计算如下[5]：

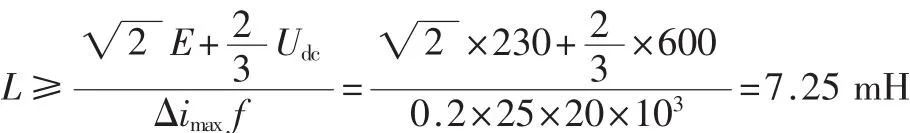
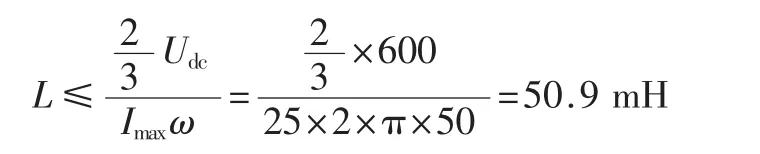
取可变电感参数变化范围分别为7.25 mH～50.09 mH和7.25 mH～14.01 mH，与取值为8 mH的不变参数电感进行对比分析。

为了便于对不变电感和数字电感的波形进行分析，仿真时间设置为10 s，前5 s电感保持定值为8 mH，5 s～10 s电感按照设置的要求变化。当电流过零点时，取最小值；当电流到达峰值时，取最大值。

3 仿真结果与分析

PSCAD软件仿真电源上升时间为0.05 s，取稳态时间在4.96 s～5.04 s范围内，电感变化前后的a相电流波形进行分析。

3.1 电感参数在7.25 mH～50.09 mH范围内变化

(1)取可调所有32个档位，a相电流波形如图2所示。

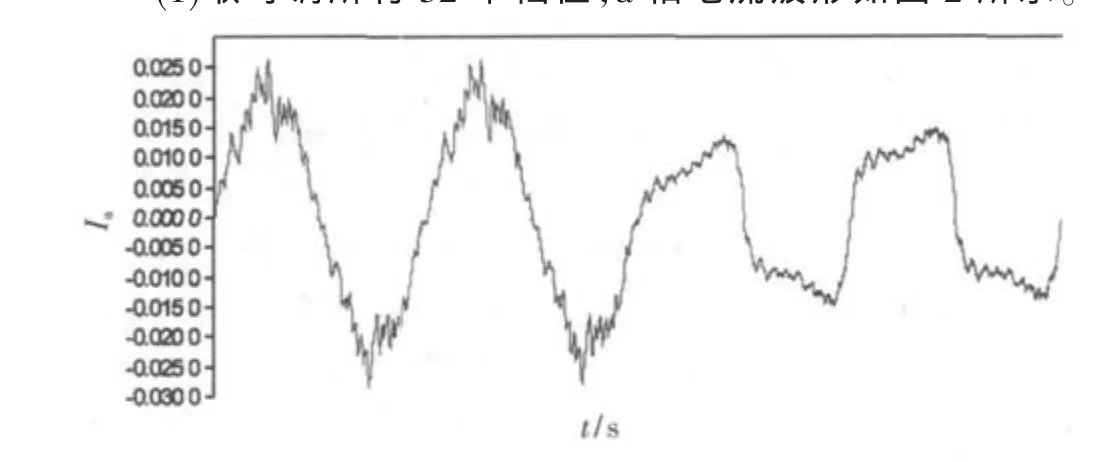
图2 电感变化前后a相电流波形(7.25 mH～50.09 mH，最小增量)

(2)取可调6个档位，a相电流波形如图3所示。

图3 电感变化前后a相电流波形(7.25 mH～50.09 mH，较大增量)

由图2、图3可见，电感参数的变化范围不宜过大，档位增量调整较小为好。

3.2 电感参数在7.25 mH～14.01 mH范围内变化

考虑到数字电容的变化范围并且按照电感取值尽可能小的原则，取可变电感参数变化范围为7.25 mH～14.01 mH，与取值为8 mH的不变参数电感进行对比分析。

(1)取可调所有32个档位，a相电流波形如图4所示。

由图4波形可见，峰值时的谐波电流明显减少。

(2)电感变化前后畸变因数分析。

输入电流畸变因数随时间的变化如图5所示。由图5可明显看出，在调整为可变参数电感后，输入电流峰值时的畸变因数明显小于固定参数电感。

(3)电感变化前后输入电流的快速响应分析。

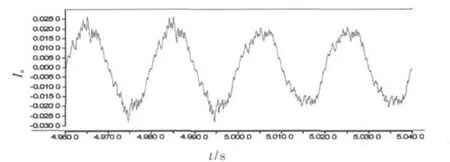
图4 电感变化前后a相电流波形(7.25 mH～14.01 mH，最小增量)

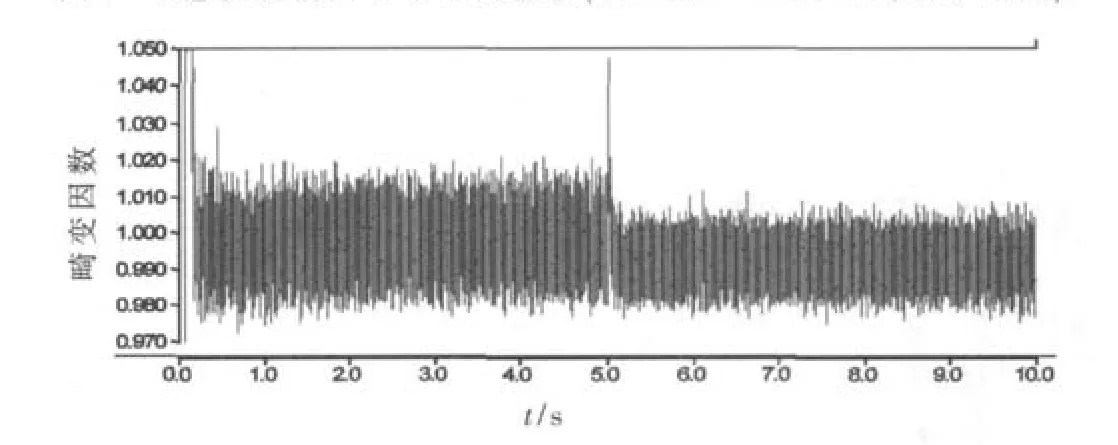
图5 输入电流总畸变率

对a相输入电流求导后列出部分过零点电流导数数据如表1所示。

表1 a相电流求导数据

由表中数据可见，电感参数可调后电流的快速跟踪性能得到了改善。

使用PSCAD软件，建立了基于同步旋转坐标系下的直接电流控制方法和双闭环控制结构的电压型PWM整流器的仿真模型。提出了利用数控电感替代传统的电感线圈，使得电感可在线调整来改善电流环的动、静态响应。仿真结果表明，采用新元件后，既可以较好地实现电流过零点的快速跟踪，又可以达到抑制电流峰值点时谐波电流的目的，在改善电能质量方面具有一定的实用价值。

[1]钟炎平，沈颂华.PWM整流器的一种快速电流控制方法[J].中国电机工程学报，2005，25(12)：52-56.

[2]BLASKO V，KAURA V.A new mathematical model and control of a three-phase ac-dc voltage source converter[J].IEEE Transactions on Power E1ectronics，1997，12(1)：l16-123．

[3]吴庆彪.基于dSPACE的PWM整流器的研究[D].上海：东华大学，2010.

[4]张岭，谷志锋，尹志勇.动态电压恢复器同步基准正弦电路设计实现[J].电子设计工程，2010(11)：33-36.

[5]Li Yuanzheng.储能系统中PWM整流器的研究[D].武汉：武汉理工大学，2009.