正态型指标的Bayes可靠性验证试验设计★

冯文哲，刘琦

（国防科学技术大学信息系统与管理学院，湖南 长沙 410073）

1 引言

装备的高可靠性是其完成任务的必要保障条件，而对装备的可靠性指标进行验证是装备研制的一项关键技术要求。在试验实施之前，进行试验设计是装备试验管理的一个重要环节。可靠性的统计验证试验方案设计就是在假设检验的基础上，通过对两类风险 （生产方风险和使用方风险）或性能水平需求进行分析，设计与权衡设计方案，用尽可能少的试验来获取足够有效的信息，对装备的可靠性做出统计推断[1]。随着装备设计制造技术的发展，现代武器装备研制、生产和试验的费用越来越高，怎样在充分利用已有各类信息的条件下，降低装备的现场试验费用，是试验管理者长期以来重点关注的问题。由于Bayes方法可以充分利用装备的各类验前信息、样本信息和总体信息，完成对装备可靠性的评估分析。因此，与经典的验证试验设计方法相比，可以节约样本量和试验时间，从而降低试验成本[2]，所以Bayes方法在装备试验评价中有着广泛的应用。

正态分布作为统计学中的一个重要分布族，在装备的可靠性分析中也有着大量的应用，并且有大量的学者在这方面进行了深入的研究。在正态分布的可靠性分析方面，Anna[3]通过对失效率服从正态分布的传送带进行了可靠性试验分析，给出了系统可靠性的计算方法；美国的Mil-Hdbk-338b[4]给出了寿命服从正态分布的产品的可靠性分析判断技术，并且以微波管和机械器件为例，进行了实例说明。Liu Changhong[5]对可靠性分布函数的确定进行了研究，以正态分布为例进行了详细的说明。刘琦[6]等对基于液体火箭发动机性能试验数据服从正态分布的情况，运用Bayes方法对正态分布天地试验条件下的环境因子进行了分析；在可靠性验证试验设计方面，W.S.Lin[7]对磨损量服从正态分布的切割工具的可靠性进行了试验设计及分析；Yang Luo[8]对结构参数服从正态分布的可靠性试验设计进行了研究；荣吉利[9]等针对性能参数服从正态分布的一类航天火工机构，参照 “应力-强度”模型，提出了一种强化试验的小子样可靠性验证方法；郑波[10]等对于不合格率服从正态分布的火工品，推导出了可靠性试验验证的样本量确定方法；张硕云[11]对简单假设情况下，可靠性参数服从正态分布的试验设计进行了研究，并且给出了满足两类风险要求的最小样本量求解方法，但是对于复杂假设的情况没有研究。

从现有的研究情况看，在小子样条件下，基于Bayes方法对于正态分布参数的假设检验，是基于损失函数，选择试验验后损失达到最小的假设，而对接受或者拒绝原假设时，弃真或者采伪的概率（即两类风险）关注得较少。从统计分析的角度来看，基于小概率事件原理[12]，在考虑两类风险的条件下，选择正确的检验假设，对于使用方和生产方而言都是比较有益的，而且在装备生产定型后，可以降低事故的发生比例。这比单纯采用损失函数来决定假设检验的结论更科学、合理。

本文结合装备试验鉴定的这一需求，针对可靠性参数服从正态分布的装备或产品，在复杂假设的情况下，基于Bayes理论，以验后两类风险为目标建立了可靠性验证试验设计的非线性约束规划模型，并基于0-1损失函数对两类风险的计算进行了推导。最后结合示例，对寿命服从正态分布的xx型号部件进行可靠性验证试验设计，给出了基于两类风险的可靠性统计试验方案的分析与求解过程。

2 样本量计算的非线性约束规划模型

在可靠性分析中，有些产品的寿命或者维修时间服从正态分布，记为N （μ，σ2）。对于可靠性分析，可转化为对期望μ的假设检验。记统计假设为：

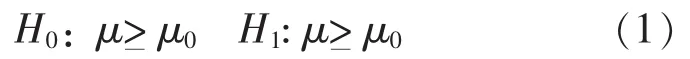
式 （1）中：μ0——研制合同中规定的可靠性要求，比如MTBF的最小值。

根据统计学理论[12]，在给定原假设和备择假设的条件下，试验中获得的样本量越大，统计推断的结果就越可信，对应的两类风险 （弃真、采伪风险）也越小。而任何试验都需要一定的经费支持，并且由于抽样检验存在的不确定性，会对今后的使用、设计生产等造成一定的影响，所以在进行试验设计时，可将试验经费、两类风险要求进行综合考虑，从而建立如下的损失模型。

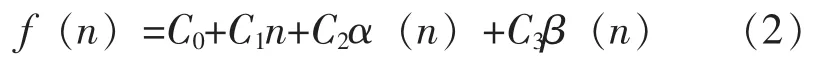
式 （2）中：C0——进行试验所需的初始试验费用，包括试验场地建设费用、人员培训费用、管理费用等；

C1——试验每台设备或者产品所需的费用，包括设备的购买费用、燃料消耗费用、试验与管理人员工资等；

n——产品现场试验所需的样本量；

α（n）——现场试验样本量为n时，运用Bayes方法进行假设检验，所造成的生产方的弃真风险；

β（n）——现场试验样本量为n时，运用Bayes方法进行假设检验，所造成的使用方的采伪风险；

C2——在H0正确的条件下，如果拒绝原假设H0，所造成的生产方的损失，包括产品的重新设计与生产延误、销售市场的萎缩等；

C3——在H0不成立的条件下，如果采纳原假设H0，所造成的使用方的损失，包括产品使用过程中的维护保障、任务延迟损失等。

上述模型只是考虑损失的一个简单的线性模型，在实际使用中，可根据实际情况考虑与两类风险、试验费用相关的各种损失，建立比较全面的损失模型。

通常情况下，在研制合同中，研制方和使用方会规定两类风险的最大值，即给定α0，β0，并要求由于产品的试验不可能无限制地进行下去，所以研制方和使用方通常会给定现场试验的最大次数N。为了保证将来产品使用的安全性、可靠性，并且通常要求现场试验次数大于等于某一给定的最小试验次数n0，从而给定现场试验次数的约束条件

装备试验设计的目的是在满足两类风险要求的前提下，使得试验损失达到最小。所以，可建立如下的非线性约束规划模型：

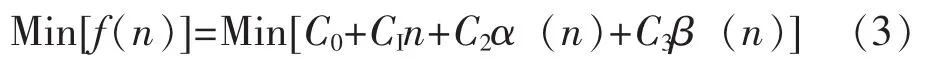
约束条件为：

利用Bayes方法，进行试验设计，就是结合装备的关于μ的验前信息，在满足式 （4）条件下，选择使式 （3）成立的最小的现场试验次数n。

3 基于 Bayes方法的 α （n）、 β （n）的计算

假设某产品的寿命服从正态分布N（μ，σ2），其中方差σ2已知，对参数μ作假设检验 （式1）。在Bayes分析中，通常是基于损失函数进行假设检验，选择使得验后损失达到最小的原假设或者备择假设。0-1损失函数是Bayes方法中应用较为广泛的一种损失函数，所以在此采用0-1损失函数[2]进行分析。设损失函数为：

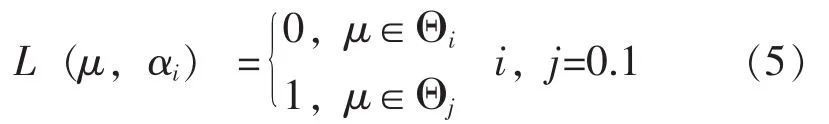
式（5）中：αi(i=0,1)——采纳假设Hi的行为；

μ——上述正态分布中的参数；

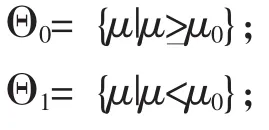
Θ=Θ0∪Θ1， Θ0∩Θ1=Φ， Θ 为参数空间， 取Θ=(-∞，∞)，Θ0，Θ1为Θ的一个分划。

设X=(x1,x2,…,xn)为对总体进行抽样所得到的样本，按照验后期望损失最小的原则可得Bayes决策不等式[13]为：

式 （6）中：acc H0——接纳原假设；

acc H1——接纳备择假设。

取 μ 的验前分布 π (μ) 为正态分布 N(θ,τ2)， 其中超参数θ,τ2已知，否则可通过验前分布确定的相关计算方法得到，如工程意义法、专家信息法等[2]计算得到。由样本X，可得似然函数为：

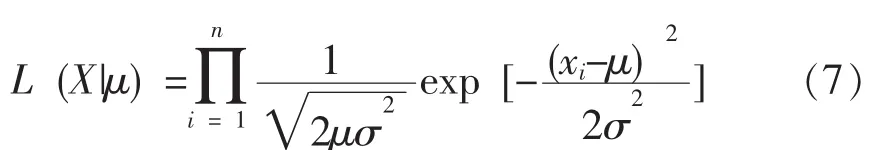
由Bayes公式，可得м的验后分布为：

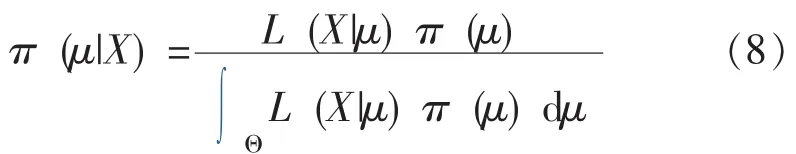
由于 N(θ,τ2)是 μ 的共轭分布[2]， 所以， π(μ|X) 仍为正态分布， 记为 N(θ1,)， 其中：

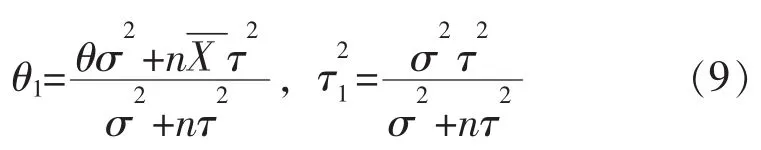
考虑到检验的假设式 （1），从而有

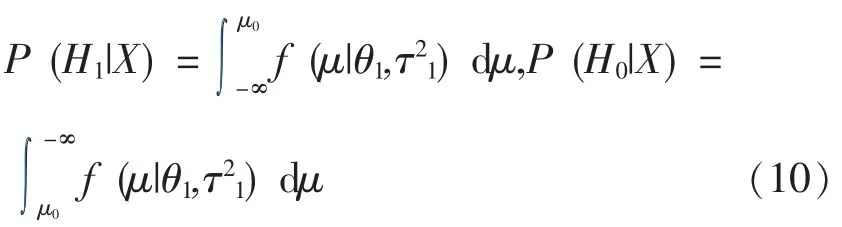
式 （10）中：f(μ|θ1,)——正态分布N(θ1,)的密度函数。

记A为：

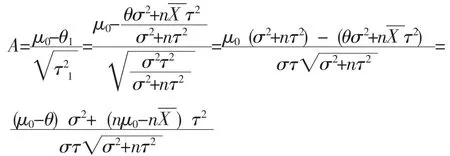
则 P(H1|X)=Φ (A)， P(H0|X)=1-Φ (A)。 其中，为标准正态分布的分布函数。

从而有

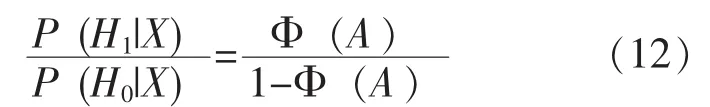
由于 A＝0 时， Φ （A） ＝1－Φ （A） ＝0.5。 联合式 （6）、 （12）， 可得如下的决策不等式：

从而可得拒绝原假设的拒绝域为：

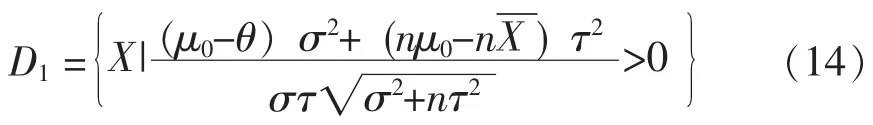
即

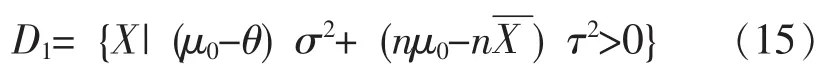
由式 （15），可得接受备择假设H1的抽样结果应满足：

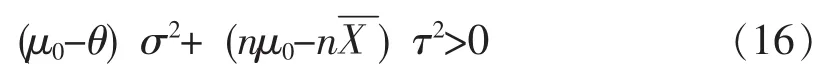
定义决策临界值为：

从而有：

进一步计算可得采纳原假设H0的区域D0为：

根据数理统计[12]的相关理论，可知样本均值服从正态分布N(μ,σ2/n)，在Bayes假设检验的情况下，犯两类错误的概率为：

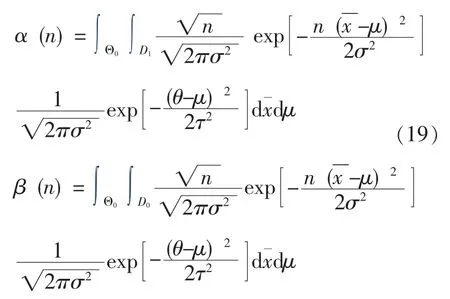
例 1 假定 θ=5001.2，τ2=5.7788， 即取 π (μ)为 N(5001.2，5.7788)， 并假定 σ2=64，μ0=5000。由式 （19）计算，可得不同样本量n条件下两类风险的具体取值，如图1所示。

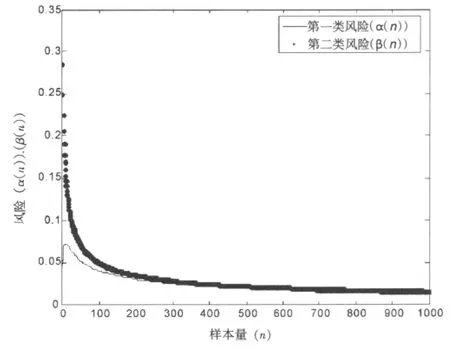
图1 样本量与两类风险的关系图

从图1可以看出，第二类风险随着样本量的增加而严格地递减，第一类风险在刚开始有上升趋势，这只是在极小样本时产生的波动问题，但是变化幅度并不大，随后也是严格地递减，这是符合实际情况的。

4 基于Matlab最优试验方案的求解

由于Matlab[14]具备强大的计算功能，能进行复杂的积分运算，因此在N不大的条件下，可采用Matlab进行枚举计算， 选择满足式 （3）、 （4）要求的最小的现场试验次数n。计算步骤如下：

a） Step 1 根据实际情况选择 C0， C1， C2， C3，α0， β0和 n0， N 的具体数值。

b）Step 2根据验前信息，包括历史试验数据、子系统信息、专家信息和仿真信息等确定μ验前分布，确定θ,τ2的具体数值。

c）Step 3选择n=N， 由式 （19） 计算 α （n），β （n） 并判断： 若 α （n）， β（n） 满足式 （4）， 则继续下面的步骤；否则，说明现有的信息和样本量还不能满足最低的检验条件，需修改约束条件 （4）或者收集更多的验前信息，修改验前分布，然后转Step 1。

d）Step 4定义损失的初始值CT=C0+C1N+C2α(N)+C3β (N)+1。

e） Step 5 取 n=n0。

f） Step 6 由式 （19） 计算 α （n）， β （n）， 若α （n）， β （n） 满足式 （4）， 则由式 （2） 计算 f（n）， 并判断： 若 f（n） ＜CT， 则记 nC=n为当前最优的试验次数，MC=μ0+(μ0-θ) σ2/(nCτ2) 为决策的临界值， 取 CT=f（nc），n=n+1， 继续进行 Step 6；若 α （n）， β （n） 不满足式 （4）， 则取 n： =n+1，继续进行Step 6。

通过上述的循环计算，即可得到最优的试验次数nC和决策的临界值MC。试验实施时，安排进行nC次试验。试验完毕后，计算样本均值，并进行判断，若样本的试验结果X∈D1则拒绝原假设，否则不能拒绝原假设。

4 示例分析

例2假设xx型号产品的寿命服从正态分布N(μ,64)，假设使用方要求该部件的寿命不能低于5000 h，如果规定的两类风险为α0=0.10，β0=0.15，试给出验证试验设计方案。

a）验前分布超参数的估计

在本项目研究中，对于正态分布中方差σ2已知的情况，取正态分布N(θ,τ2)为期望μ的共轭验前分布，其参数可采用工程意义法来确定。当具有多批验前试验数据时，也可采用下述方法来估计超参数。

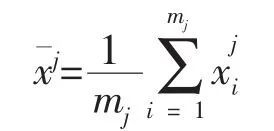
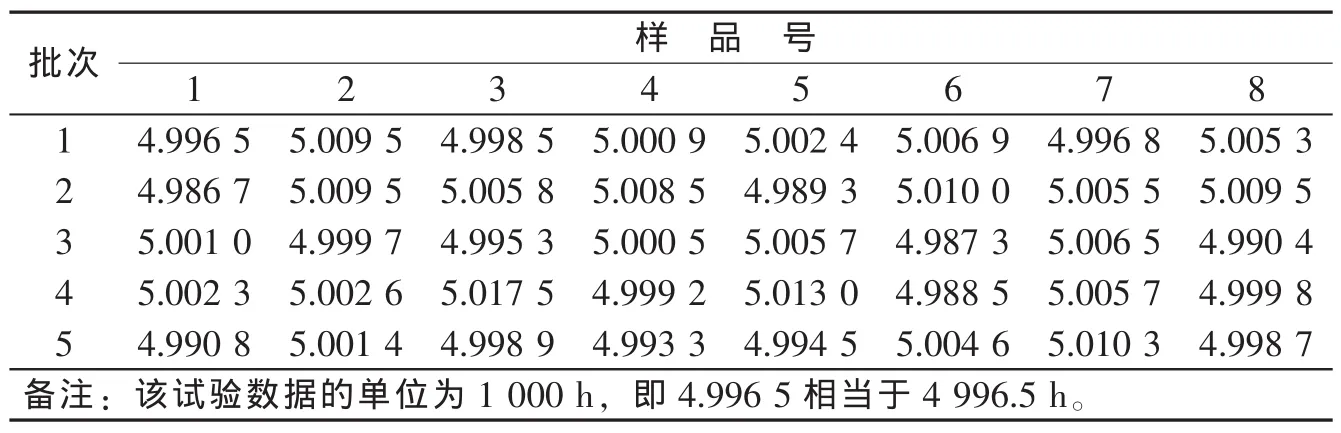
表1 XX产品多批次寿命数据表

超参数θ和τ2的估计为：

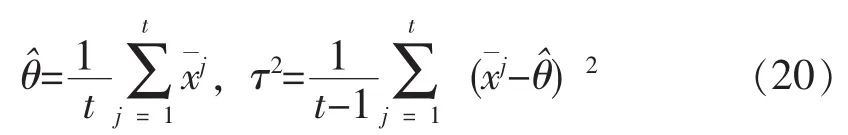
b）最小样本量的求解

根据题意对参数做出如下检验假设：

由式 （17），可得决策临界值为 M=5000-13.29/n，从而可得接受域和拒绝域分别为：

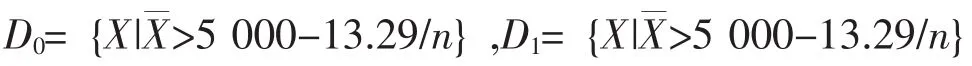
在本例中，若选择n0=1，N=1000，C0=100，C1=30， C2=40000， C3=30000， 则可得 nC=57， 此时MC=4999.7668，f(57)=5782.4954。此时实际的α(57)=0.0489，β(57)=0.0660。

损失随试验次数n的变化情况如图2所示。表3列出了不同现场试验次数下的两类风险与损失的计算结果。

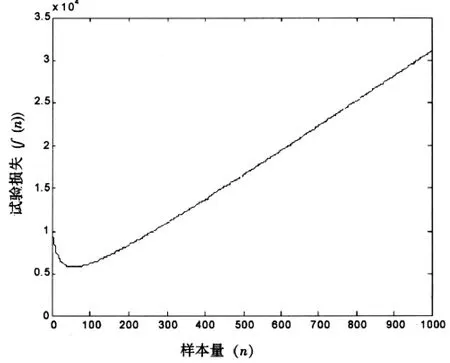
图2 样本量与损失的关系图

表2 验前均值的参数估计

当 n0=1， N=1000， C0=100， C1=30， C2=40000，C3=50000时,则可得 nC=72，此时 MC=4999.8154， f(72)=7023.5662。 α (72)=0.0458，β(72)=0.0587。 当n0=1，N=1000， C0=100， C1=1000 000，C2=1，C3=1时,则可得nC=10，此时实际的α(10)=0.0727，β(10)=0.1471。

分析上述计算结果可以看出，损失模型中的系数 (C0，C1，C2，C3)不一样时，同样的样本量所对应的损失是不一样的，所得出的最优样本量也不一样。这就说明，对于一个损失模型来说，系数的确定非常重要，当系数选取恰当时，可以准确地对试验方案进行评价，从而挑选出最优试验方案，为装备的验收鉴定提供决策依据。因此，在进行试验设计时，应通过充分、全面的市场调研与分析，给出各系数一精确取值，从而确保得到优化的试验设计方案。

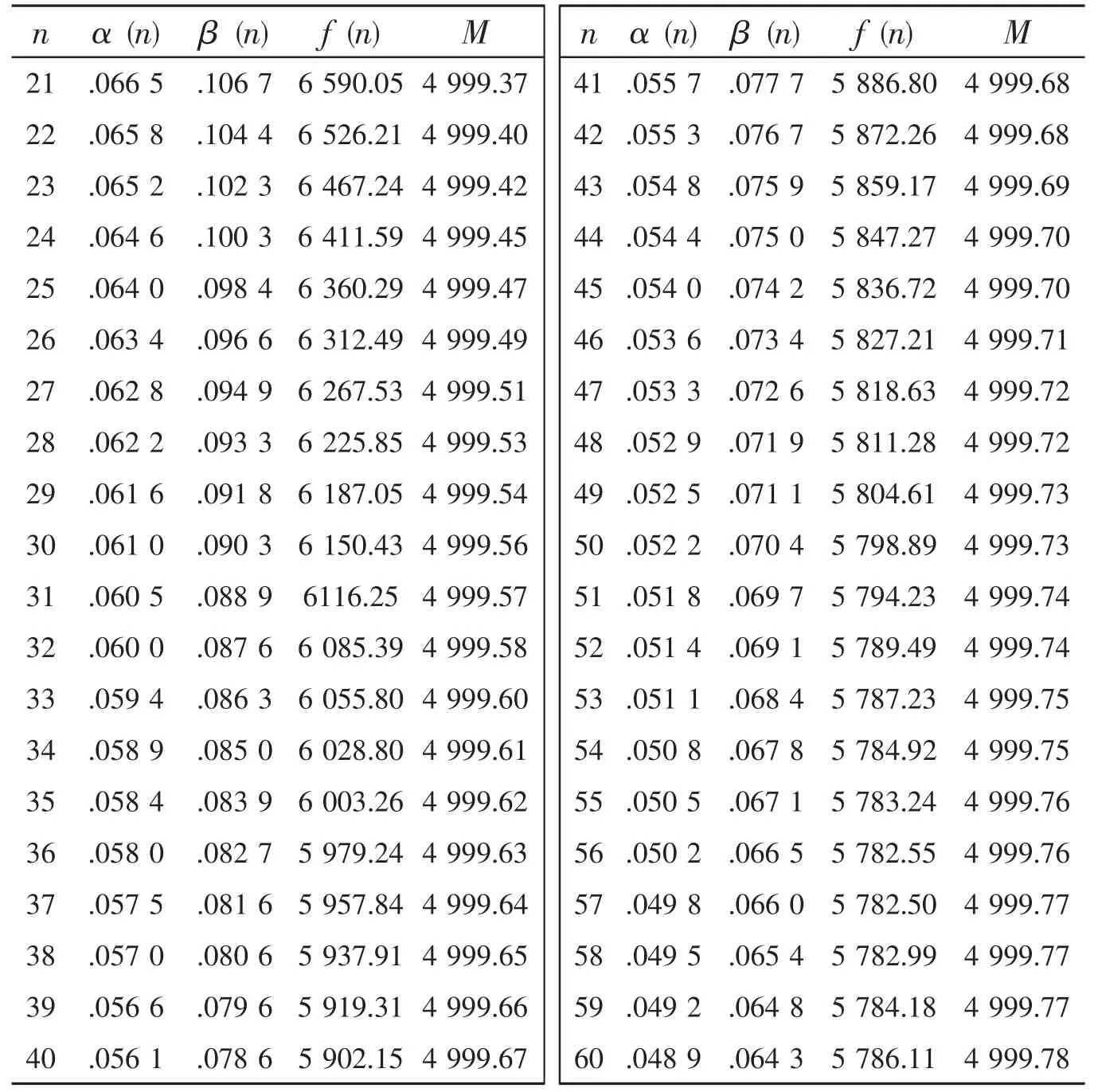
表3 不同现场试验次数下的两类风险与损失

6 结束语

本文根据Bayes理论，在两类风险的要求下，对装备战技指标服从正态分布条件下的可靠性的验证试验设计进行了研究，建立了满足两类风险的最小样本量的非线性约束模型；基于0-1损失函数，按照验后风险最小的原则，推导出了两类风险的计算公式，并基于Matlab给出了最小样本量的计算步骤。这种方法的运用很好地解决了正态分布参数基于两类风险的可靠性验证试验设计问题，但在具体的应用过程中可在如下方面进行进一步的研究：

a）对于具体的可靠性验证试验，如何根据待试验的装备、现有的试验条件以及该装备在未来作战中担负的职能等因素来确定试验的初始费用、单个样本的试验成本以及由于试验所带来的决策风险而导致的期望损失，从而确定模型中的系数C0，C1， C2， C3。

b）本文仅对可靠性指标服从正态分布的情况进行了研究，当装备的可靠性指标服从二项分布、指数分布或者其它分布类型时，可以按照本文的研究方法，对其可靠性验证试验方案进行设计。

c）为了便于计算，本文选用0-1损失函数对问题进行讨论。0-1损失函数的假设比较简单，在具体的应用中，可以根据实际情况来选择合适的损失函数，构建更加准确的损失模型，从而找到最优的试验方案。

[1] Patrick D.T.O'connor.实用可靠性工程 [M].北京：电子工业出版社,2005.

[2] 武小悦,刘琦.装备试验与评价[M].北京：国防工业出版社,2008.

[3] Anna Pavlisková.Reliability and continuous regeneration model[J].Acta Montanistica Slovaca Roník,2006， (2):119-121.

[4] MIl-HDBK-338b-1998，Electronic reliability design handbook[S].

[5] LIUChang-hong,LIUXin-tian,Wang Ren-liang.The analysis of the distribution of the failure statistical data hydrogen-adjacent pipelines[J].Manufacturing Science and Engineering,2010,(2):909-912.

[6] 刘琦,冯静,周经伦.火箭发动机性能可靠性的Bayes分析 [J].中国空间科学技术,2003,(6)：46-51.

[7] LIN W S.The reliability analysis of cutting tools in the HSM processes[J].Archives of Materials Science and Engineering,2008,30(2)：97-100.

[8]LUO Yang,LIANG.Robert.Incorporating set-up into reliability-based design of driven piles in clay[J].Canadian Geotechnical Journal,2006,43(9)：946-955.

[9] 荣吉利,张涛.航天火工机构可靠性的强化试验验证方法[J].宇航学报,2009,30(6)：2426-2430.

[10] 郑波,柳维旗,许和贵.一种确定火工品贮存可靠性试验样本量的方法 [J].火工品,2005,(2)：28-30.

[11] 张硕云,武小悦,刘琦.基于两类风险的正态分布Bayesian试验样本量 [J].航空计算技术,2008,38(5):11-17.

[12] 武小悦,刘琦.应用统计学 [M].长沙：国防科技大学出版社,2009.

[13] 张金槐,刘琦,冯静.Bayesian试验分析方法 [M].长沙:国防科技大学出版社,2007.

[14] 张志涌.精通MATLAB 6.5版 [M].北京：北京航空航天大学出版社,2003.