牛顿求解第一宇宙速度思想的启示
2011-03-20窦文浩
窦文浩
(广州市第二中学 广东 广州 510530)
在讲解“万有引力定律”的内容时,计算星球的第一宇宙速度是一个重点.计算的方法通常是由万有引力提供向心力,根据匀速圆周运动的规律求解.而牛顿在求解星球的第一宇宙速度的时候,用了巧妙的比例和几何方法,体现了微分的思想;同时,是对“月 -地检验”思考的结果.在中学物理教材中,都会提到牛顿的“月-地检验”,而在教学中没有能很好地阐述这一思想的光辉之处.很好地理解牛顿的原始思想,对认识万有引力以及牛顿第一定律具有很大启示意义.同时,在求解高中常常涉及的万有引力习题时,也能开拓新的思路.
1 常规方法求解星体的第一宇宙速度
【例1】求解一质量为M,半径为R的球形星体的第一宇宙速度.
解析:如图1所示,设卫星质量为m,绕星球做匀速圆周运动,轨道半径为r,则有
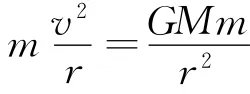
解得

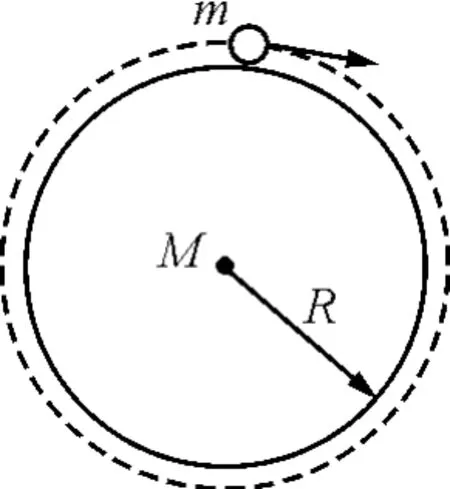
图1
根据第一宇宙速度的意义知,v应当是卫星绕球形星体做匀速圆周运动刚好不落地时的速度,则r=R,于是

2 牛顿的思想求解第一宇宙速度[1]
【例2】在地球上,一个物体做平抛运动时,至少需要多大的初速度才不会落回地面?
解析:首先要假定地球是一个半径为R的球体,如图2.假设在A点平抛一物体,平抛运动竖直方向的分运动是自由落体运动.当水平方向位移为x,即半个弦长DB,而竖直方向恰好下落s,即AD高度;平抛的物体恰好不碰到地面,此平抛的初速度即为第一宇宙速度.如下求解此速度.
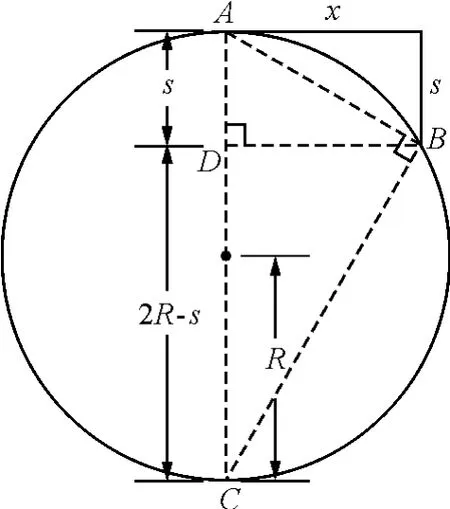
图2
取1 s的时间,则物体的运动即为严格的平抛运动,而各数量关系依然如图2所示,则由几何关系知△ADB∽ △BDC ,故有

在地球表面,1 s内物体自由下落的高度约为5 m,即s=5 m;2R是地球的直径,远远大于s,故
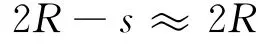
所以
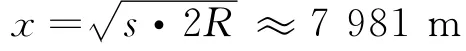
所以平抛的初速度(即第一宇宙速度)
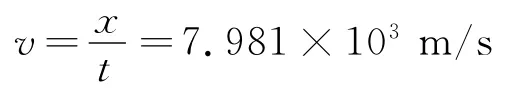
牛顿利用其发现的“牛顿第一运动定律”推断,若月球不受外力,则其将沿轨道的切线运动下去,而它却下落了(只是没有落到地球上),轨迹是一段圆弧,类似平抛的轨迹.那么反过来,在地球上一物体的平抛,如果速度恰当(足够大),则其轨迹将如月球的轨迹一样,是一个圆,这个恰当的速度就是第一宇宙速度.这就是牛顿“月-地检验”的思考.上述的解题步骤正是依据这一思想.当然,在1 s内月球“下落”的高度与地球表面平抛物体“下落”的高度是不同的,但成比例,比例关系正是满足牛顿所总结出的平方反比定律.
点评:
(1)牛顿的方法看似比常规方法复杂,却体现了最一般的推理过程:利用牛顿第一定律,揭示了圆周运动所蕴涵的力的作用特点—— 指向有心力的力心.
(2)在计算的处理中,利用微分近似代替的思想,将看似两种不同的运动即平抛运动与圆周运动统一起来,化曲为直.同时,略去无穷小量,体现了微分近似代替思想的精髓.
(3)用最简单的规律,加上巧妙的数学处理手段,是物理竞赛中常常应用的方法,正是物理所要培养的思维品质.
3 牛顿的方法在常规教学中的体现
3. 1 平抛运动的实质
如图3[2]所示,从地球上某一高塔处平抛一小球,初速度分别为v1,v2,v3和v4,则其运动的轨迹分别为1,2,3和4;这些轨迹都是以地球的质心为一个焦点的椭圆.
(1)轨迹1,2是假定地球物质全部集中在质心处时才可能的轨迹.实际情况中,抛体不可能完整地进行这一椭圆运动,这一轨迹与地球表面的交点就是落地点.可见,物体平抛运动的轨迹实质上是此椭圆轨迹的一部分.
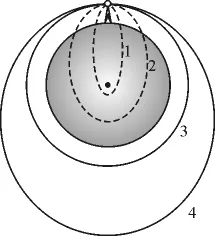
图3
(2)轨迹3是一个圆轨迹,可以看做是两焦点重合的一个椭圆,它是轨迹2向轨迹4过渡时即地球质心作为下焦点向作为上焦点过渡时,焦点在地球质心重合的情况.塔高相比地球的尺度,是可以忽略的,故轨迹3的半径就是地球半径,v3就是第一宇宙速度.
3. 2 牛顿思想的应用
【例3】如图4所示,两颗地球卫星运行轨道分别为1和2,两轨道在P点相切,则在切点处,1号卫星和2号卫星的速度大小关系如何?
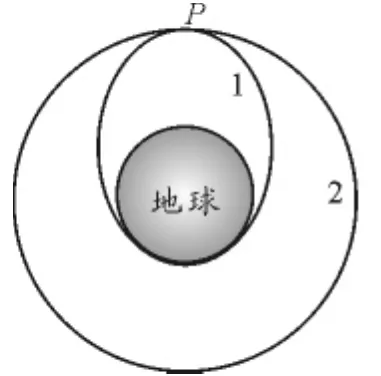
图4
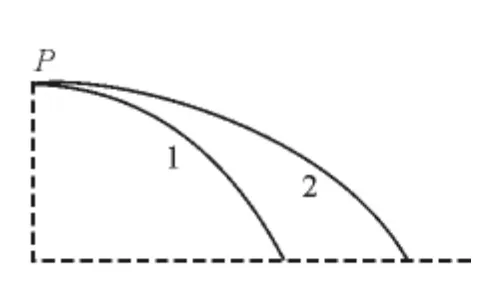
图5
解析:可以把P点附近的轨迹放大,如图5所示.根据牛顿的思想,则图5所示的两条轨迹即为两平抛运动的轨迹(当然,这里的重力加速度g不再是地球表面的值).那么,根据平抛运动的规律,在同一高度抛出的两物体,初速度越大的,水平射程越大;可以得知,在P点2号卫星的速度大于1号卫星的速度.
1 (美)费恩曼.费恩曼物理学讲义(第一卷).上海:上海科学技术出版社,2005.70
2 (美)休D·杨,罗杰 A·费里德曼.西尔斯物理学(上册).北京:机械工业出版社,2008.367
