基于APDL语言的网架结构优化设计
2011-03-17孟文清程倩张亚鹏
孟文清,程倩,张亚鹏
(河北工程大学土木工程学院,河北邯郸056038)
网架结构是平面呈平板状,由杆件按照一定的规律布置,通过节点连接而成的一种空间杆系结构,已被广泛应用在大型公共建筑、工业厂房、大型机库、特种结构、装饰网架、扩建增层等不同领域中。在保证结构安全的条件下,如何最大限度地减轻结构的重量,减少结构的工程造价是当前网架结构优化设计的研究热点[1-4]。目前对空间网架结构的优化通常采取以下两个途径:一是在结构类型和几何外型已定的条件下对截面尺寸的优化,如:李新坤采用遗传算法对网架结构的杆件截面积优化进行了比较[4];蔡建良利用差商法以杆件截面积为离散变量对网架结构进行静力和动力优化[5];二是对于结构参数如网格数、网架高度等进行的优化,王福成、冯瑛等分别利用遗传算法对网架高度进行了研究,结果表明在不同类型、不同跨度下,网架最优高度对结构重量也有不同程度的影响[6-7]。
然而由于网架结构涉及的参数较多,特别是参数间的量级或量纲不同,所以针对网架高度与杆件截面尺寸的综合优化鲜见于文献。本文将网架高度按照建筑模数进行离散化,利用APDL语言编制以一维搜索算法和改进应力比法为设计准则的优化程序,对网架结构进行同一量纲下的多变量综合优化设计。
1 基本原理
结合一维搜索算法与改进的应力比法进行离散变量的优化设计。
一维搜索算法的基本思想是把设计变量按离散集的升序排列,同时在保证目标函数是设计变量的单调递增函数,以及约束函数是设计变量的单调递减函数的前提下(一般空间结构容易满足),依次将设计变量的离散集的第一个截面代入约束条件,若约束条件不满足,则检查下一个截面,直到所有的约束条件满足为止[8]。
由于应力比法是一种基于连续变量的方法,因此需要对应力比法进行改进使其适用于离散变量的优化,称之为改进应力比法。应力比法是对结构进行整体分析后得到其应力分布,为使各杆件材料能够得到充分发挥,将结构分为若干部分,通过修改各部分设计变量,进行分步优化,经过重新拼合得到新的结构,从而完成一次优化循环,经过这样不断的优化循环直至满足要求为止[9]。
2 工程概况
某加油站屋盖采用平面尺寸为24m×30m的斜放四角锥网架,网格数为8×10,网格尺寸为2.121m×2.121m,屋面板为太空网架板,两面坡排水,屋面坡度3%。杆件材料选用Q235钢管,节点采用螺栓球节点,网架俯视图见图1。
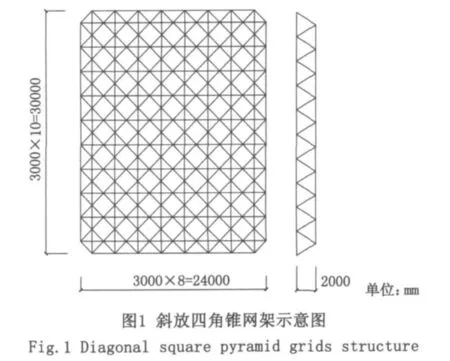
3 数学模型
网架高度、杆件截面等因素对结构的静力特性及耗钢量都有较大影响;另外,网架平面尺寸一定后,网架高度的大小不仅直接影响腹杆与弦杆的夹角,还影响杆件的内力与腹杆的经济性。由此分析可知,考虑工程具体建筑功能及其他条件要求,建立的优化数学模型:
其中,W—每平米用钢量,kg/m2;ρ—材料的质量密度,kg/m3;l—杆件长度;θ—腹杆与下弦平面所成的角度;A—杆件截面积;i—上、下弦杆件编号; j—斜杆杆件编号。
⑵设计变量:以网架高度 Z以及杆件截面A为设计变量X=[Z,A]
⑶约束条件:
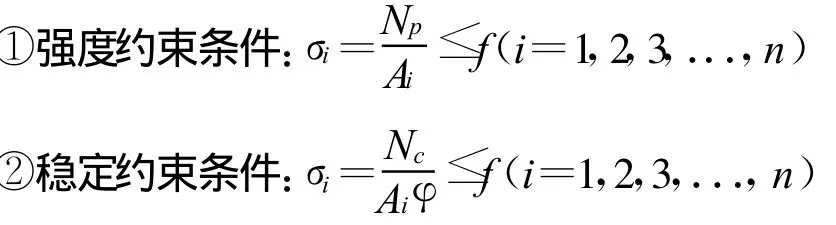
其中,Np—杆件的拉力;Nc—杆件的压力; λ—长细比;φ—轴心受压杆件的稳定系数,按照钢结构设计规范选取。

③刚度约束条件:λi≤[λ](i=1,2,3,..., n),其中:[λ]为容许长细比,压杆[λ]=180,拉杆[λ]=250。
其中:Di—第i根杆的应力比;fy—抗拉强度; Dmin,Dmax—应力比的上,下限。
⑥高度约束:根据《网架结构设计手册》[11]中所规定的网架跨高比范围选取,Zi∈[Z1,Z2,…, Zm](i=1,2,3,...,m)。
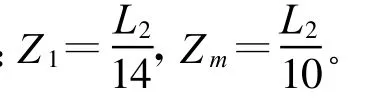
⑦杆件截面约束:杆件截面面积 A是离散型变量,在给定的规格化截面中选取且钢管规格不宜小于φ 48×2。
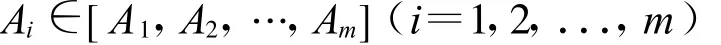
其中,Ai—第i个杆件的截面积;[A1,A2,…, Am]—给定的杆件截面积的集合,且Area(φ 48×2)≤Ai。
4 离散优化
网架高度按照一定的步长变化使其符合建筑模数,与杆件截面同时作为离散设计变量进行优化。本文采用一维搜索算法和改进应力比法对网架结构进行优化。为方便后面的杆件截面优化,在建立模型之前先建立一个钢管截面的规格表(表1),该表通过四个一维数组来实现,分别包括钢管的内径、外径、回转半径和截面面积。钢管表中的钢管面积应该遵循单向递增的原则[12]。
4.1 构建网架结构模型
建模时使用有限元软件ANSYS10.0,考虑网架节点只传递轴力,所以杆件单元类型选择三维杆Link8单元,这种单元可以模拟弹性材料的拉伸、压缩,因而可以模拟网架结构杆件。上弦周边节点铰接。利用APDL语言的循环语句建立网架模型[13]。
4.2 初始条件与基本参数选取
该工程网架的初始设计高度Z=1.715m,弹性模量E=2.1×105N/mm2,泊松比ρ=0.3。
4.3 施加荷载并进行静力分析
该工程实际施加荷载为均布荷载,由于荷载的方向竖直向下无法施加单元荷载,本文采用简化方法将其转化为施加在节点上的集中荷载,即将均布荷载转化为线荷载,再将线荷载转化为集中荷载[12]。本工程屋面恒载取0.85kN/m2,活荷载取0.5kN/m2,雪荷载取0.4kN/m2,取两者较大值,即0.5kN/m2。
荷载施加结束后,进行杆件的内力分析。
4.4 后处理
在计算内力的基础上,根据前面所述的数学模型的要求,提取各杆件内力,求得各杆应力比、长细比,通过使用循环语句来判断是否满足约束条件进而对网架进行校核。
4.5 迭代循环
网架结构为超静定结构,当网架跨度与网格尺寸确定时,高度、杆件截面积与杆件内力有关,经过迭代循环后才能得到优化结果。本文利用EDELE命令删除杆件单元,NUMCMP命令压缩各杆件单元,进入前处理后,重新建立 Zi+1=Zi+ 0.1的网架模型,投入下一次循环迭代。
4.6 输出优化结果
使用APDL语言中*VWRITE命令将各高度下,杆件应力比数组中的数据按照指定格式写入数据文件中,用*CFOPEN命令打开,再按照指定的数据格式输出应力比结果及杆件总质量[14]。
4.7 优化结果分析
按照上述过程进行网架结构优化,计算结果见表2。图1表明,将高度对结构耗钢量也具有较明显的影响。原设计方案数据见表2。本文提供的优化方法较原设计节省钢材约为14.17%,最大应力比为0.9781,最大位移为74.05mm,满足规范要求。方案1是对原结构仅进行杆件截面优化结果见表2,优化效果约为4.1%低于本文提供的优化方法。因此该方法优化效果较明显,具有一定的优越性与可行性。
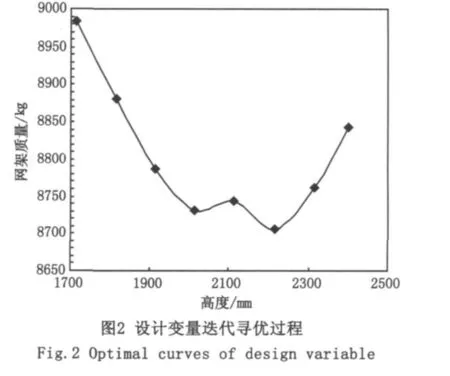
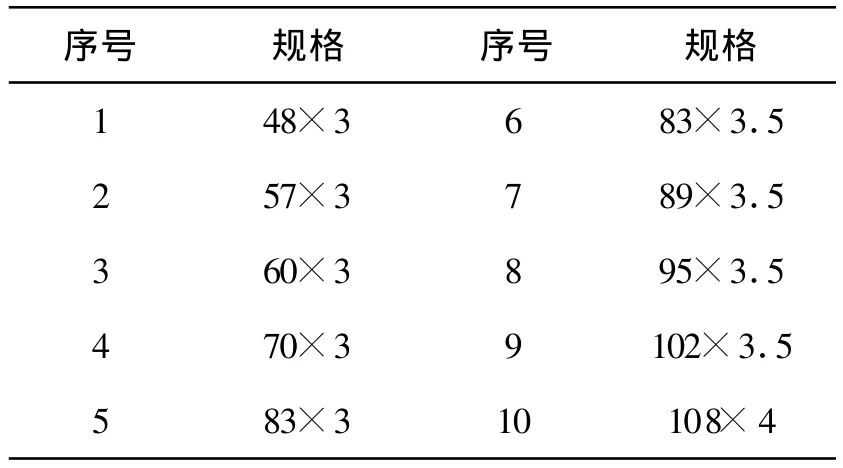
表1 选用钢管规格表Tab.1 Use steel specifications
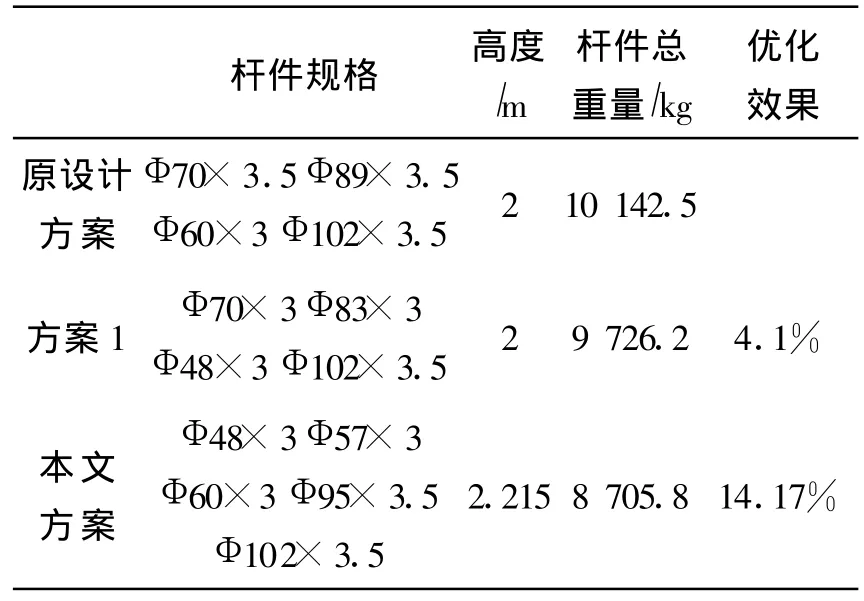
表2 各优化设计结果比较Tab.2 Optimization results and comparison
由于空间网架结构的最大特点是节点和杆件很有规律,因此利用APDL语言的循环命令可以方便的实现网架模型的建立、施加荷载、提取参数等过程;利用循环判断语句[12]则可以快速的实现约束条件判断等优化循环过程,并且使用这种参数化语言更易于对结构模型的修改和维护,省去繁琐的建模、加荷等过程,极大地提高了工作效率。通过使用APDL语言的*VWRITE命令读入整个优化文件并进行优化分析的方式,使分析任务更加简单有效。
5 结论
APDL语言可以大大减少修改模型和重分析的工作量,实现了基于离散变量的优化。优化后节省钢材约为14.17%,可为同类工程优化设计提供参考。
[1]张春玉,赵延林,陈勇.混合变量遗传算法在预应力网架结构中的应用[J].黑龙江科技学院学报,2009, 19(4):306-309.
[2]张春玉,韩雪,姜封国.基于系统可靠度的预应力空间网格结构优化[J].黑龙江科技学院学报,2009,19 (5):377-379.
[3]谈若明,肖建春,韩志刚.空间网格结构的多参数优化设计[J].空间结构,2009,15(2):58-61.
[4]李新坤.遗传算法及其在网架结构优化中的应用研究[D].西安:西安理工大学,2010.
[5]蔡建良.基于离散变量网架结构优化设计研究[D].镇江:江苏大学,2006.
[6]王福成.遗传算法的网架结构优化研究[D].大庆:大庆石油学院,2007.
[7]冯瑛.网架结构优化设计分析[D].西安:西安建筑科技大学,2008.
[8]孙焕纯,柴山,王跃方.离散变量结构优化设计[M].大连:大连理工大学出版社,1995.
[9]牟在根,侯晓武,宁平华,等.ANSYS环境下基于离散变量的网架结构优化设计[J].北京科技大学学报, 2006,28(5):417-421.
[10]GB50017-2003,钢结构设计规范[S].
[11]《网架结构设计手册》编辑委员会.网架结构设计手册[M].北京:中国建筑工业出版社,1998.
[12]刘文静,李黎,杨德喜,等.ANSYS环境下的网壳结构优化设计[J].空间结构,2008,14(2):39-41.
[13]陈志华,刘红波,周婷,等.空间结构APDL参数化计算与分析[M].北京:中国水利水电出版社,2009.
[14]邢海东,徐国杉,郝际平,等.基于ANSYS二次开发的网架结构优化设计[J].空间结构,2007,13(2):41 -43.
