框剪结构动力时程分析的精细积分法
2011-03-17胡启平王颖
胡启平,王颖
(河北工程大学土木工程学院,河北邯郸056038)
近年来,随着建筑的高度不断增加,建筑结构在地震作用下的变形越来越大。目前,国内外许多学者普遍采用动力时程分析法对高层建筑结构的地震响应进行研究[1-3],然而在求解过程中,一方面采用有限单元法计算单元刚度矩阵时,通常会产生较大的累计误差;另外在求解结构的动力方程时,采用只具有一阶或二阶精度的传统Newmark-β和Wilson-θ法,往往导致计算结果精度较低,尤其是在高频阶段。对此,钟万勰等[4-6]提出了哈密顿对偶体系及求解动力方程的精细积分法,并得到地震反应下的高精度数值解。在此基础上,本文采用哈密顿体系中的区段混合能矩阵推导结构的层单元刚度矩阵,利用有限元刚度集成法形成总刚矩阵,并采用初值问题的精细积分法求解结构地震作用下的动力方程,以进一步提高得到的地震响应数值解的计算精度。
1 基本假定
框剪结构是以框架和剪力墙两种类型的抗侧力单元组成的结构体系,在高层建筑结构中应用非常广泛。框剪结构一般看作是平面结构,将同一方向布置的所有框架合并成综合框架,所有剪力墙合并成综合剪力墙。框剪结构中的综合框架和综合剪力墙通过楼板协同工作,共同抵抗水平力。假定框剪结构由综合框架和综合剪力墙两个抗侧力单元构成,每个抗侧力单元都具有弯曲和剪切变形,可看成竖放的铁摩辛柯梁,楼板是刚性的,楼板的作用沿高度连续化[7-8]。
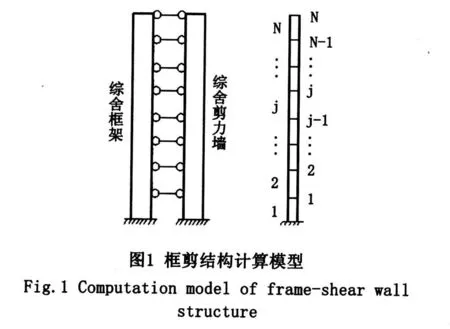
计算模型如图1所示,共有综合框架和综合剪力墙2个抗侧力单元,其抗弯刚度分别为D1= E1I1和D2=E2I2,抗推刚度为 C1和C2,综合框架和综合剪力墙的截面转角为θ1和θ2,侧移为v1和v2,由于刚性楼板的作用,综合框架和综合剪力墙协同工作,v1=v2=v。抗侧力结构上作用的总的水平外载集度为q=q1+q2。
2 框剪结构协同分析的哈密顿体系
框剪结构协同分析[6]时的拉格朗日函数为
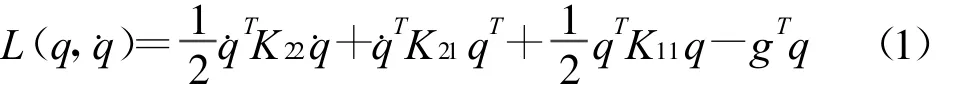
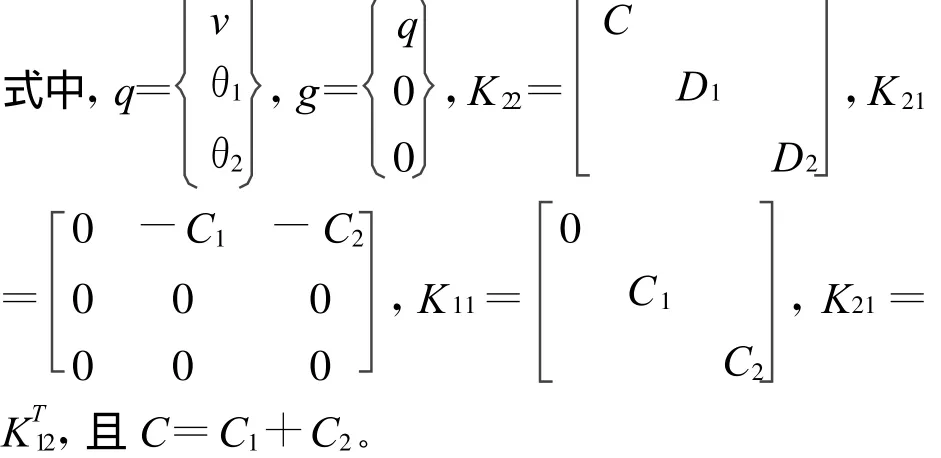
通过引入q的对偶变量p=K22﹒q+K21q,可导出哈密顿函数[9-10]:
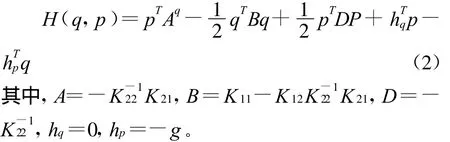
3 框剪结构的刚度矩阵
框剪结构被看作顶部自由,底部固定的并联悬臂铁摩辛柯梁模型[8],结构的单元刚度矩阵利用两端边值问题精细积分法中区段混合能矩阵F,G,Q来表示[6]。
将结构沿高度按楼层分为若干单元(区段),通过精细积分法中区段混合能矩阵与哈密顿常数矩阵A,B,D的关系,得到第j个单元(区段)的混合能矩阵Fj,Gj,Qj。
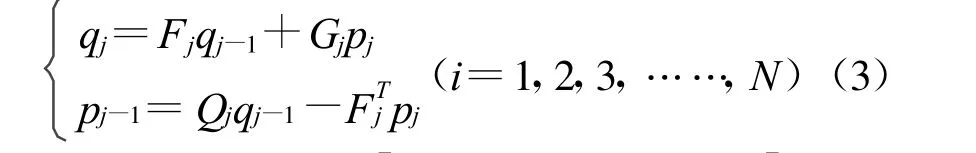
通过混合能矩阵与节点位移和力的关系,可得到每层楼(结构单元)的刚度矩阵
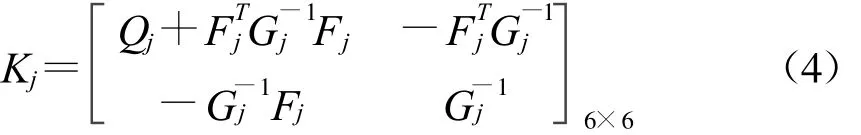
利用有限元刚度集成法形成总刚矩阵,并引入顶部自由,底部固定的边界条件,则结构整体刚度矩阵为K=
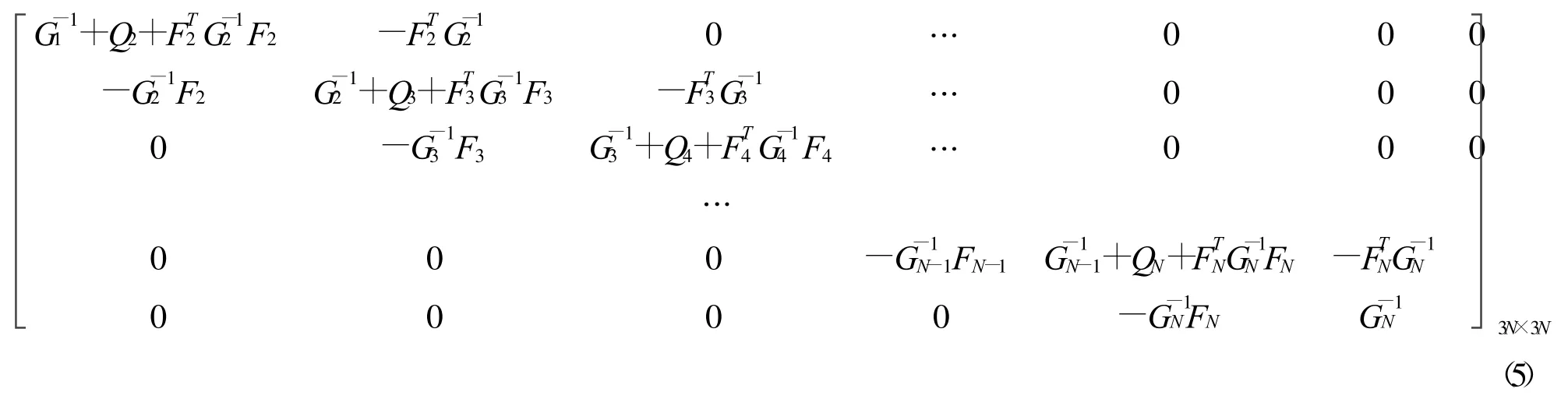
4 质量及阻尼矩阵
建立结构的动力方程,必须考虑结构的质量分布及阻尼。
4.1 质量矩阵
本文采用多质点体系模型,将结构的质量集中于楼层处,其特点是质量矩阵与位移向量相对应且是对角矩阵,每一层有3个自由度。则
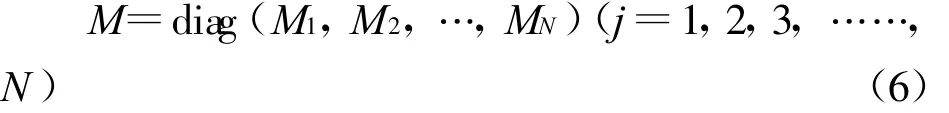
其中,Mj=diag(ρ Ajhj,ρ INjhj,ρ Ifjhj);ρ—结构材料密度;N—结构总层数。
4.2 阻尼矩阵
计算中采用瑞雷(Rayleigh)阻尼,结构阻尼矩阵的计算公式为

5 数值计算
利用初值问题的精细积分法进行框剪结构的地震反应分析,由以上分析可得框剪结构的动力方程
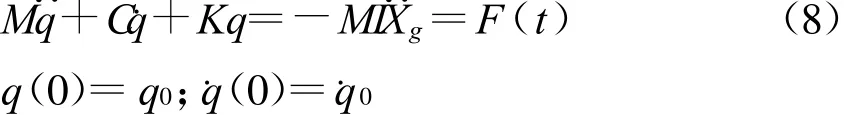
将上式进行降阶处理,转化为

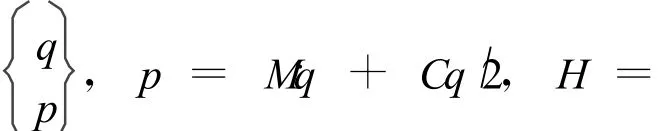
若将荷载作用时间分成时间步长为地震波时间步长η的若干时间间隔,则式 (9)的解可表示为
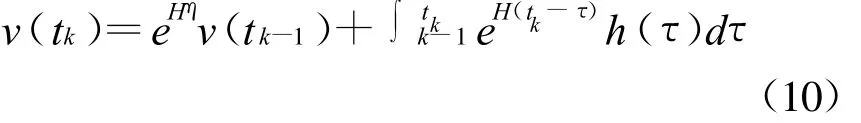
上面具体的降阶转化及式(10)中指数矩阵和特解的计算参见文献[12-14],将初值v(t0)代入,采用迭代法可依次求出每时刻tk对应的未知量。
6 算例验证
某一框剪结构平面图如图2所示:层高均为3m,共19层,总高度为57m,1~5层柱取700mm× 700mm,剪力墙厚度300mm,混凝土强度等级为C35;6-12层柱取600mm×600mm,剪力墙厚取250mm,混凝土强度等级为C30;13~19层柱取500mm×500mm,剪力墙厚200mm,混凝土强度等级为C25;梁截面分别为250mm×500mm,300mm× 600mm,混凝土强度等级为 C25;楼层板厚为120mm,混凝土强度等级为C20;结构的材料密度取为2.5×103kg/m3。
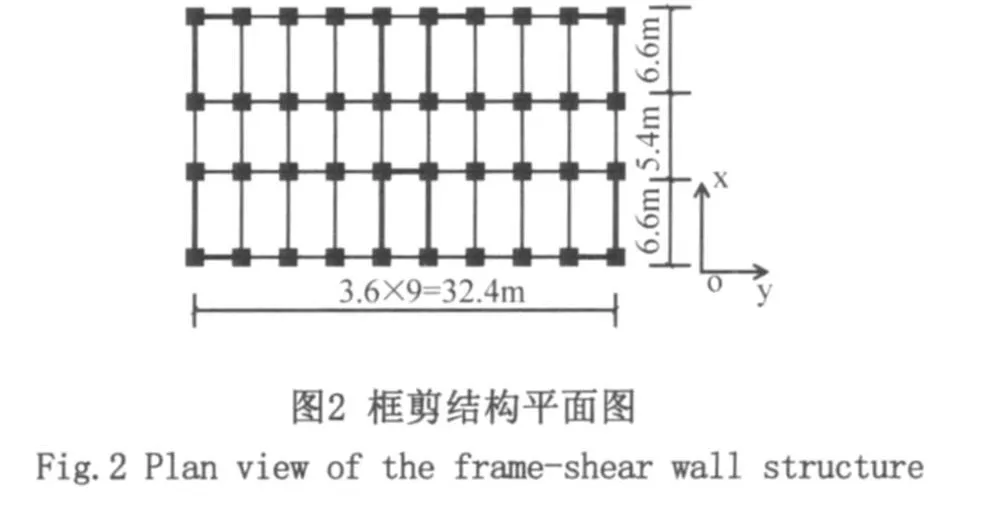
对上述框剪结构进行动力时程分析。地震波采用美国加利福尼亚州EI-Centro地震记录,峰值为341.7cm/s2,在本例中,地震波沿x方向作用于结构上,持续时间0~8s,时间步长为 Δ t=0.02s,在常遇烈度7度下,选定加速度峰值为35cm/s2。
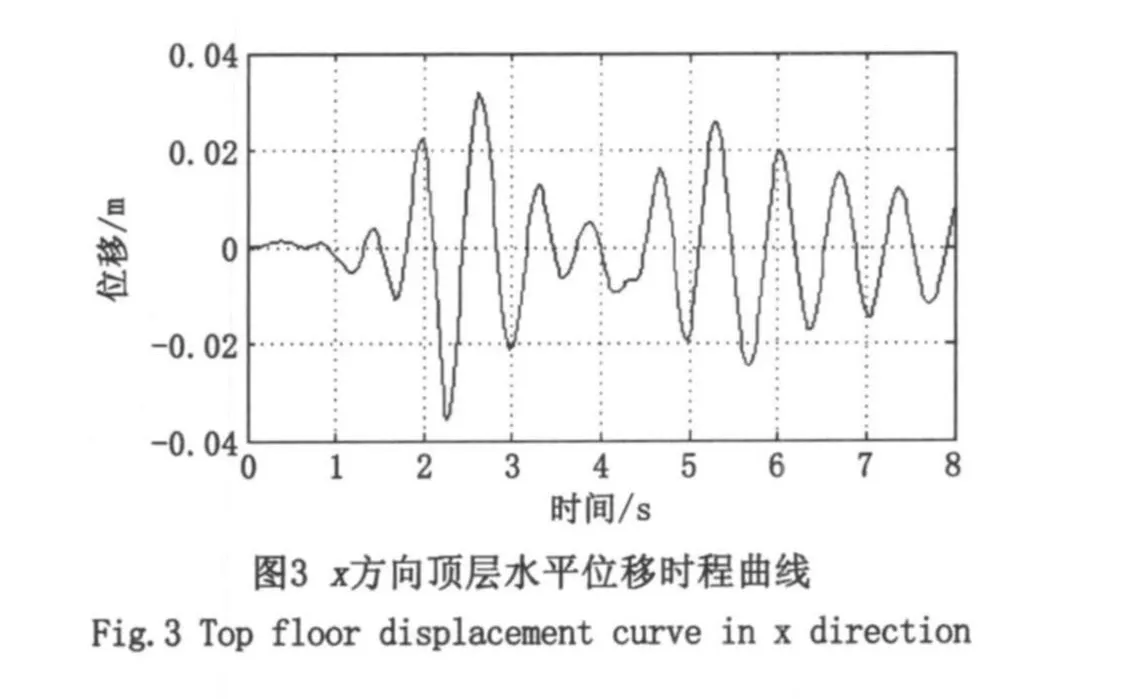
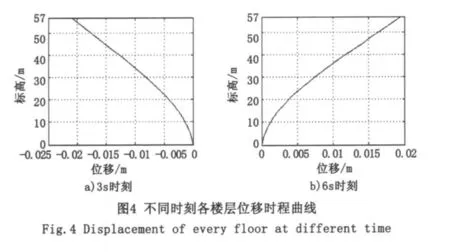
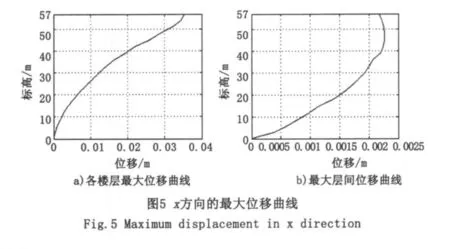
利用本文编制的MATLAB语言程序对上述框剪结构进行动力时程分析。在多遇地震作用下,顶层时程位移最大值为35.47mm,发生在2.26s,结构位移在平衡位置附近上下变化(图3);图4是任意选择的两个时刻各楼层的位移时程曲线,结构位移变化符合结构的地震动时刻反应情况;图5中a图表明结构的整体位移曲线呈现弯剪型,符合框剪结构的变形特点;而从b图可得出结构的层间最大位移角为1/1 329,满足现行规范中规定的高度不大于150m的框架-剪力墙高层建筑结构弹性层间位移角限值(1/800)的要求,且结构没有出现明显的薄弱层,表明整个结构是处在弹性工作的状态。
7 结论
1)运用两端边值问题精细积分法中的区段混合能概念推导结构的单元刚度矩阵,避免了传统有限单元法中误差积累的现象,得到的结果更符合实际。
2)初值问题的精细积分法,比传统的Newarkβ,Wilson-θ离散积分法得到的结果精度更高。
[1]CLOUGH R W,BENUSKA K L,WILLSON E L.Inelastic earthquake response of tall building[C].Proceedings of the Third World Conference on Earthquake Engineering,New Zealand:[s.n.],1965.
[2]汪梦浦,沈蒲生.钢筋混凝土高层结构非线性地震反应分析现状[J].世界地震工程,1998,14(2):1-8.
[3]沈小璞,肖卓.高层建筑结构动力时程响应的状态空间迭代法[J].建筑结构学报,1998,26(2):67-69.
[4]钟万勰.结构动力方程的精细时程积分法[J].大连理工大学学报,1994,34(2):131-136.
[5]汪梦浦,周锡元.结构动力方程的更新精细积分法[J].力学学报,2004,36(2):191-195.
[6]钟万勰.应用力学对偶体系[M].北京:科学出版社, 2002.
[7]侯瑞珀.基于并联剪弯梁模型的高层建筑结构协同分析[D].邯郸:河北工程大学,2006.
[8]高洪俊,王羡农,闫亚光.框剪结构协同分析的状态空间法[J].西安科技大学学报,2007,27(4):573-574.
[9]钟万勰.应用力学的辛数学方法[M].北京:高等教育出版社,2006.
[10]胡启平,李张苗,侯瑞珀.铁摩辛柯梁弯曲问题的对偶求解体系[J].河北工程大学学报(自然科学版), 2006,23(3):1-4.
[11]包世华.高层建筑结构计算[M].北京:高等教育出版社,1991.
[12]汪梦浦,周锡元.结构动力方程的高斯精细时程积分法[J].工程力学,2004,21(4):13-16.
[13]胡启平,刘鹏,吕铭.考虑部分楼板变形时框-剪结构的协同分析[J].河北工程大学学报(自然科学版),2009,26(3):4-7.
[14]胡启平,孙良鑫,高洪俊.铁摩辛柯梁弯曲问题的精细积分法[J].工业建筑,2007,37(s1):268-270.
