雷诺应力与流场旋度的关联分析

陈庆义,汤勇,高音

(大连海洋大学海洋工程学院,辽宁大连116023)

雷诺应力与流场旋度的关联分析

陈庆义,汤勇,高音

(大连海洋大学海洋工程学院,辽宁大连116023)

基于雷诺时均方程导出了含有雷诺应力的涡量微分方程。对于充分发展湍流流动在高雷诺数弱非定常条件下,从平衡角度分析雷诺应力与时均流场涡量及速度的关系,得出雷诺应力与时均流场的涡量和速度的耦合作用是相关联的,反映流场结构的涡量的演化能够间接表示湍流动能的输运和耗散过程。在标准κ-ε模型中,对其本构方程加入涡量张量和变形速度张量使其非线性化后,改善了对正应力的计算,并能预示二次流的存在。

雷诺应力;κ-ε模型;涡量;本构方程

湍流在数学上处理起来十分困难的主要原因是,即使在边界条件非常简单的流动中,运动的长度尺度和时间尺度变化范围都很宽。湍流不仅是一种有涡流动,而且不同尺度旋涡之间的相互作用并不相同[1]。旋涡相互作用的理论主要有Bossinesq-Parandtl-Taylor等的涡黏性假说。涡黏性模型实际上是一个旋涡尺度大小分得很开的相互作用模型,而涡黏性概念构成了已有湍流模型的基础,这些湍流模型都离不开经验或半经验假定。目前,两个应用比较广泛的模型是混合长度模型和κ-ε模型。用定义变量中一个长度尺度和一个时间尺度较成功地说明了许多湍流流动的主要特征已属不易,而标准κ-ε模型是典型的两方程模型,并被广泛应用于工程实际中。为了提高标准κ-ε模型在一些无界限流动、强旋转流动和管道的充分发展流动中的预测能力,出现了一些修正的κ-ε模型,如典型的(RNG)κ-ε模型和Realizable κ-ε模型[2]。这些模型的主要特点是,在湍流动能κ及其耗散率ε的输运方程中考虑了涡量的作用,改进了κ-ε模型对湍流应力各向异性的计算[3]。尽管很多专家认为,雷诺应力方程模型(RSM)是能发展成具有真正通用性的经典湍流模型,但在非线性模型领域中的最新进展也使两方程模型的研究逐步深入和完善。在这类模型中,将雷诺应力的本构方程加入速度梯度乘积的非线性项,以改变雷诺应力与流场速度梯度的线性关系。现有的研究中,一般是假定一种雷诺应力本构方程的非线性形式,用数值模拟典型流动来检验其有效性,并修改参数值,但关于加入哪种非线性项在理论上更加合理尚未见报道。为此,作者在对非线性项选择的基础上进行了理论研究,对于不可压缩流体,从雷诺方程平衡的角度分析了雷诺应力与时均流场涡量的关联性。

1 两个漩涡运动积分恒等式

引理 设函数L(A)满足

L(A+B)=L(A)+L(B),

L(λA)=λL(A),

则在表面为S的空间区域E上,推广的Gauss公式

对于速度为V、旋度为Ω的流场,将引理应用于L(▽)=(Ω·▽)V时,▽前的Ω并不满足常量的条件,但Ω满足条件▽·Ω=0,上式仍成立。下面给出直角坐标系下的证明。

同理,对于不可压缩流体,▽·V=0,有

此二式为纯运动学形式,对于理想流体和黏性流体都是正确的。

2 基于雷诺时均方程的涡量方程

应用雷诺条件对Navier-stokes运动方程施行时间平均计算。对于不可压流体,雷诺方程为

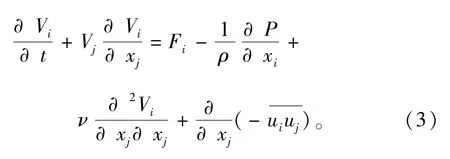
式中:ν为运动粘度;ρ为流体密度。雷诺应力的出现仅仅是因为把速度场分成了平均运动和脉动两部分,这并不代表任何新的物理机制。以τij代表雷诺应力张量,将式(3)改写成矢量形式:

对式(4)两端进行▽×(·)运算,对于有势质量力,考虑到

得到基于雷诺方程并含有雷诺应力张量的涡量动量方程为

或

3 雷诺应力与流场旋度的关联

3.1 雷诺应力散度表达式的分析

选择平均流动的特征速度U、特征长度L和特征时间T,得到式(5)的无因次形式为

式中:St(St=L/TU)为平均流场的Strouhal数, Re(Re=UL/ν)为Reynolds数,若定义特征时间T =L/U,则St=1。为了不引起歧义,上式中各变量未做改写,均表示无因次量。

大漩涡的特征速度θ和特征长度l分别用单位质量流体脉动动能κ和单位质量流体脉动动能的耗散率ε的量纲分析表达式来定义,即θ=和l=/ε是与平均流动的速度U和长度L同量级的。在高Re下,用这些大涡的尺度与运动黏性组成的大涡雷诺数(θl/ν)也是一个大的数值,所以这些大涡受惯性效应支配而黏性效应可以忽略。脉动的作用相对于黏性作用占主导地位。有关实验表明,采用涡黏性概念的话,湍流涡黏性系数是分子黏性系数μ的几万倍[5],1/ReΔΩ项体现了分子黏性的效应,相对于涡黏性作用是小量。湍流本质上是非定常的,对于充分发展的湍流时均流场,Kolmogorov(1941)的普遍均衡理论表明,较小的漩涡从大漩涡接收能量的速率,非常接近于最小漩涡动能耗散为热的速率,这样,整个湍流场就可以在这种极端条件下维持时均流动的相对稳定性。如拟序结构猝发后,能在小的时间尺度下看成时均流动是准定常的。因此,在式(6)中略去项和

因此,必存在一标量势函数Π满足

或

依据散度的物理意义,▽·τij为一矢量,表示τij在3个正交方向上相对于体积的变化。▽Π实际上是无旋的质量力(如重力)和压力梯度的作用。对于整个流场而言,雷诺应力的正应力的各向异性及切应力的对称性表明,▽·τij不可能是无旋的(在个别时刻可能存在▽·τij是无旋的点),所以从平衡的角度分析,模型化τij时,不必考虑无旋的质量力和压力梯度,只考虑流场的时均运动量,如式(7)中显含旋度Ω。因此,在模型化τij时,考虑流场旋度是合理的。

3.2 涡量和速度的耦合演化关系

采用欧拉观点在表面为S的空间区域E上写出对应的积分方程

这里应用了式(1)和式(2),式(8)左端的物理意义不明确,也很复杂,但总体上可看成是仅与雷诺应力有关的一阶张量在控制体E内的总和。对于式(8)中的(Ω·▽)V,在直角坐标系下作如下分析:

其中:l沿Ω方向;α、β、γ分别为▽Vx、▽Vy、▽Vz与l的夹角。由此看出,(Ω·▽)V表示速度沿Ω方向的变化,所以

图1 速度沿涡量方向的变化Fig.1 The velocity change in the direction of vorticity

图2 涡量沿速度方向的变化Fig.2 The vorticity change in the direction of velocity

从运动学角度看,涡量和速度是相互作用并且耦合在一起的。一方面,涡线的拉伸、压缩及扭曲使速度发生变化;另一方面,速度的改变也会引起涡量的变化。平均流对大涡所做的拉伸功提供了维持湍流的能量,尽管小漩涡本身受稍大漩涡强烈的拉伸作用,而直接受平均流的作用要小得多。由于

动能是从大漩涡向越来越小的漩涡传下去,所以小尺度漩涡的能量从根本上还是来自于平均流。这样,用体现平均流场结构的特征量,即涡量和速度来近似表征各种尺度漩涡能量的输运和耗散是可能的。

4 雷诺应力本构方程的非线性项分析

在理论上,建立物质的本构关系时,力学中一条重要的本构公理,即客观性公理,可表述为:物质的性质不随观察者的变化而变化,也就是说,本构关系对于刚性运动的参考系具有不变性[6]。

因为实际湍流不可能与初始条件和边界条件无关,所以要确定一个不随边界形状改变的类似于分子黏性应力的表达式来代表雷诺应力是不可能的,就是说得不到不随边界条件变化的雷诺应力通用表达式[6]。但有些湍流或湍流的某些区域,初始条件和边界条件只在流场中特征时间和特征长度同数量级范围内有影响,超过这些范围的点,其雷诺应力的结构完全由某一时刻以前历史上流场中点的平均速度值确定[6]。所以,人们从未放弃对某些类型的湍流,或湍流的某些区域列出雷诺应力本构关系的想法。

不可压流体雷诺应力的线性本构方程式如下:

式中:μt为涡粘系数,用k将无因次化,设

则张量bij是对称的,并且其迹为零。

依据上述客观性公理,在bij的表达式中可能出现的对称且迹为零的二次非线性项有

式中:{}表示张量的迹。

很多湍流流动存在二次流,在直方管充分发展湍流流动中是存在的[7]。笔者在文献[8]中曾构造本构方程

对直方管和直圆管充分发展湍流流动进行计算,结果表明:系数A在3个正应力均未出现,说明线性项ASij对正应力无贡献;同时,非线性项B(ωimωmj-1/3{ωbmωmk}δij)能体现正应力的各向异性,并预示二次流的存在。

文献[9]中采用

经系统参数辨识后,对扩比为1.125的后台阶流动、绕方块的二维分离流动和二维U型管道内的流动进行数值模拟计算,与相应实验结果比较,数值结果均优于标准κ-ε模型。

文献[10]中采用

对直方管充分发展湍流流动进行计算,结果也表明,线性项ASij对正应力无贡献,非线性项B(ωimωmj-1/3{ωbmωmk}δij)和C(SimSmj-1/3{SbmSmk}δij)能体现正应力的各向异性,并预示二次流的存在。

以上计算结果的改进可以理解为,相对于标准κ-ε模型,将本构方程加入了流场旋度因素并将其非线性化。这方面的研究目前缺乏不同非线性模型间的比较性分析,有很多工作需要进行,其主要障碍是有关湍流的高精度实验难以进行。

5 结论

根据以上分析,可得出以下几点初步结论:

1)在高Re下充分发展的实际湍流中,拟序结构现象提示可以在弱非定常和无黏性条件下,从平衡角度分析雷诺应力与时均流场结构不随边界条件变化的本构关系。

2)时均流场的涡量与速度的演化是耦合在一

起的,以欧拉观点的任意一有限区域内的雷诺应力的演变(即湍流动能的输运和耗散)均体现在控制体内或其控制面上涡量及速度的耦合演化上。

3)将本构方程加入了流场旋度因素并将其非线性化后,能改进对正应力的计算,并能预示二次流的存在,而对于某些特殊流动应用线性本构方程是做不到的。

[1] 吴德铭,郜冶.实用计算流体力学基础[M].哈尔滨:哈尔滨工程大学出版社,2006:342-360.

[2] 王福军.计算流体动力学分析[M].北京:清华大学出版社, 2004:124.

[3] Hoffman J,Johnson C.A new approach to computationl turbulence modeling[J].Comput Methods Appl Mech Engrg,2006,195:2865 -2880.

[4] 吴望一.流体力学[M].北京:北京大学出版社,1983:31,193, 207-209.

[5] 李心铭.流体动力学[M].青岛:青岛海洋大学出版社,1996: 388.

[6] 梁在潮,陆晶.湍流雷诺应力的本构关系[J].水动力学研究与进展,2000,15A(1):8-16.

[7] Park T S,Sung H J,Suzuki K.Development of a nonlinear nearwall turbulence model for turbulent flow and heat transfer[J].Int J Heat Fluid Flow,2003,24:29-40.

[8] 陈庆义,卓永强.含有涡量张量的非线性雷诺应力本构方程[J].大连水产学院学报,2008,23(6):466-470.

[9] 钱炜祺,蔡金狮.一种新的非线性κ-ε两方程湍流模型[J].空气动力学报,1999,17(4):392-397.

[10] 陈义良.湍流计算模型[M].北京:中国科学技术大学出版社,1991:183.

The relationship analysis of Reynolds stress and vorticity

CHEN Qing-yi,TANG Yong,GAO Yin
(School of Marine Engineering,Dalian Ocean University,Dalian 116023,China)

Based on the time-averaged Reynolds equation a vorticity differential equation with Reynolds stress contained is derived.For the full development turbulence,under condition that the flow is weakly variational with relatively large Reynolds number,the relation of Reynolds stress and the time-averaged vorticity or velocity is analyzed from an angle of equilibrium.It concluded that Reynolds stress is relative to the coupling action of vorticity or velocity and the deduction of vorticity reflecting flow field structure can indirectly express the process of turbulent kinetic energy transport and its rate of dissipation.The non-lineated κ-ε model being added deformation tensor and vorticity tensor has improved the calculation of Reynolds normal stresses,and is capable of predicting the existence of second flow.

Reynolds stress;κ-ε model;vorticity;constitutive equation

2095-1388(2011)01-0083-05

O35

A

2010-12-06

国家自然科学基金资助项目(10774021);大连海洋大学校列项目(SY 2007017)

陈庆义(1964-),男,博士生,副教授。E-mail:dlhhjys@163.com