基于正弦图的计算机断层图像配准

孙晶晶 杨 民 刘静华 吴文晋

(北京航空航天大学 机械工程及自动化学院,北京 100191)

基于正弦图的计算机断层图像配准

孙晶晶 杨 民 刘静华 吴文晋

(北京航空航天大学 机械工程及自动化学院,北京 100191)

为了解决工业 X射线无损检测中图像配准的问题,以计算机断层(CT,Computerized Tomography)图像中物体的位置变化与采集的投影数据之间的理论关系为基础,提出了基于正弦图的 CT图像配准算法.该算法结合实际的投影采集系统对投影信号进行预处理,并利用投影信号的相关性寻找物体的位置变化,可以解决二维平行束和扇束投影采集方式下物体二维刚性变换的配准问题.由于提出的算法是在重建之前的投影域内进行,因此相比传统的图像域内的配准算法适用性更高,尤其当投影数据不足、质量不高、噪声较大、重建图像有严重的伪影时,该方法更加有效可靠.对某一封装零件的配准结果证明了算法的可行性.

计算机断层成像;图像配准;投影

计算机断层(CT,Computerized Tomography)图像的配准首先是在 20世纪 90年代初由医学图像处理发展起来的一个重要分支,目的是将两幅图像中具有解剖意义的诊断点和手术感兴趣的点进行匹配,以达到对病灶精确手术的目的[1-2].工业 CT应用中,也需要将测试件和标准件进行对比,以进行自动缺陷判别和多余物判别.但是由于测试件和标准件在没有标准夹具的情况下,扫描时的放置位置很难保证完全相同,从而造成待配准图像与模板图像(即标准试件的断层图像)之间产生位置上的差异,因此准确的图像配准是正确判别的基础.传统的图像配准算法[3-8]大多是基于图像域的配准,对图像质量的依赖性强.然而工业 CT检测的对象为密度较大的金属件,重建的图像存在较为严重的环形伪影、条状伪影以及噪声,这些因素会极大影响基于图像域的配准算法中极值的寻找,从而得到错误的配准结果.

为了解决上述问题,本文首先分析了 CT图像中物体的位置变化与采集的投影数据之间的理论关系[9],给出了基于正弦图的 CT图像配准算法;然后结合实际投影采集系统,分析了投影采集中常见的中心偏移以及采集条件变化问题对该算法的影响,并提出了解决方案.

本文提出的基于正弦图的 CT图像配准算法可以对二维平行束和扇束投影采集方式下两次扫描物体的相对位置变化做出准确估计,解决物体二维刚性变换的配准问题[10-11].由于本文提出的算法是在重建之前的投影域内进行的,因此相比传统的图像域内的配准适用性更高,对于投影数据不完全、散射硬化现象严重、扫描系统存在偏差的情况时也同样适用.

1 理论分析

平行束下的投影采集方式如图 1所示,扫描过程为:探测器和射线源不动,扫描台绕中心旋转,探测器采集扫描台上的物体断层在不同旋转角(这里称为投影角)下的投影数据.探测器在每个投影角下采集的投影信息为一维数据,将 360°范围内的所有投影角下的一维投影数据依次排列起来,便构成二维数据,称为正弦图.

正弦图坐标系为(s,θ),θ为当前的投影角,s为投影到旋转中心的距离,如图 2所示.经过空间某一点 (xr,yr)的投影 R[f](θr,sr)如式(1)所示[9]:

其中,δ()为 Dirac函数;u(xr,yr)为线性衰减系数 ;(θr,sr)为投影的坐标 ;θr为投影角度;sr为投影在探测器上的横向距离.

由于 CT扫描中,物体位置的变化多是在垂直于旋转轴的平面(xy平面)内,因此本文只讨论物体在 xy平面内的二维刚体运动和投影变化之间的关系.物体的二维刚性运动是通过基本的平移和旋转变换组合而成的,每一个变换都可以表示成为矩阵的形式,刚性变换则可以表示为一系列矩阵的乘积.点(xr,yr)在 xy平面内绕旋转轴 z轴转动 α角,并在 xy平面内沿方向角 β移动距离

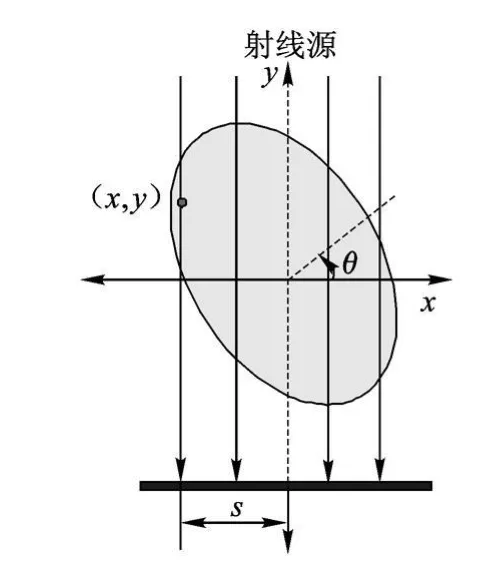
图1 平行束下的投影采集方式

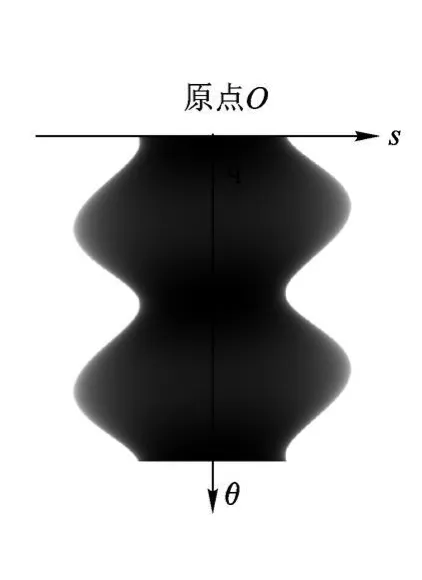
图2 正弦图及其坐标系

旋转矩阵 Rz(α)和平移矩阵 T(r,β)分别为r,坐标变为(xf,yf),相应的矩阵变换为

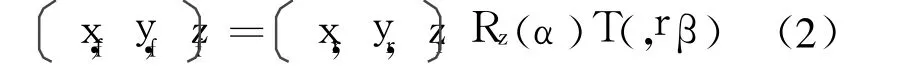
因此坐标(xr,yr)与(xf,yf)间的关系为

此时在平行束投影采集方式下,经过点(xf,yf)的投影 R[f](θf,sf)如式 (6)所示:

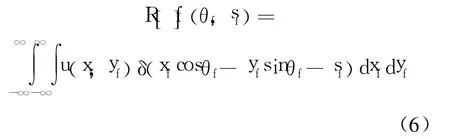
其中,u(xf,yf)表示线性衰减系数;(θf,sf)表示投影的坐标;θf表示投影角度;sf表示投影在探测器上的横向距离.

由式(1)、式 (5)、式 (6)推导可得

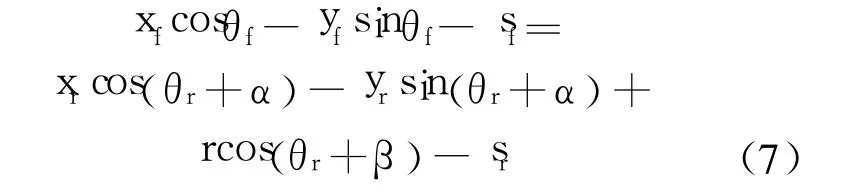
由式(7)可以总结出空间中某点(xr,yr)的投影R[f](θr,sr)和它在 xy平面内进行二维刚体变换后的点(xf,yf)的投影 R[f](θf,sf)存在着式(8)所示的关系:

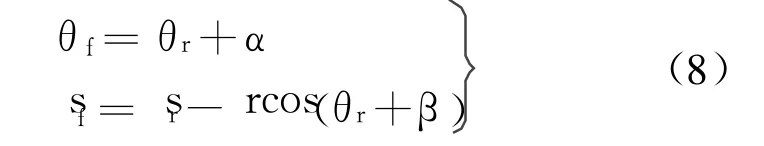
式(8)说明两幅投影的灰度曲线是一样的,只不过在 θ坐标上相差了刚性旋转变换的角度α,并且 s轴坐标之差是与平移变换的幅值、方向角有关的正弦函数.因此通过对正弦图的投影信号进行信号的自相关以及互相关分析,找到两幅正弦图信号中相关的部分,就可以得到物体二维刚性变换的参数,这也是本文基于正弦图的 CT图像配准算法的基本思路.

2 基于正弦图的配准算法

由于实际计算机断层扫描系统中存在着旋转中心偏移,采集电流、电压不稳定的情况,因此在实际采集的投影中应用信号相关运算还需要进行以下的修正:

1)CT图像的重建坐标系是以旋转中心为坐标原点的,因此如果两次采集时,系统的旋转中心存在偏移,就意味着两个重建坐标系是不同的,因此不能直接进行正弦图的配准,而是应该首先对旋转中心偏移进行校正,将两个重建坐标系放在同一个坐标原点上,才能进行后续的基于正弦图的配准;

2)由于在两次采集的过程中,射线源的电流、电压和探测器的吸收系数不能保证完全相同,因此采集到的投影虽然形状不变,但是在幅值上会有变化,为了更好地分析正弦图中信号的相似性,需要先对正弦图进行归一化处理,以背景为 0值,在[0,255]之间对正弦图进行归一化,可以大大提高相关性分析的准确性.

设工件在位置 1时采集的投影为 Pr,旋转中心偏移量为 mr,在位置 2时采集的投影为 Pf,旋转中心偏移量为 mf,两次采集的步进角均为 Δθ,每次采集投影的幅数 M=360/Δθ.本文提出的基于正弦图的 CT图像配准算法具体描述如下.

1)预处理.首先利用投影 Pr和 Pf求取各自的旋转中心偏移量 mr和,然后按照 Pr(i,j)=Pr(i,j-mr)和 Pf(i,j)=Pf(i,j-mf)进行旋转中心偏移的校正,然后将扇束扫描结构下的投影重排为平行束扫描结构下的投影,最后对正弦图进行归一化处理.

2)正弦图的相关运算分析.利用第 1节所述的待检测物在平行束投影中做刚体运动时,投影数据与位置变化之间的关系,可以首先采用自相关运算处理平行束的正弦图得到平移不变函数序列,然后利用物体旋转相当于正弦图起始位置变化的原理,利用互相关信息找到待检测正弦图和模板正弦图的对应角度,然后再次利用自相关计算找到各个角度下的投影平移距离,这样就得到了待检测物体的位置变化参数.其实现流程图如图 3所示.

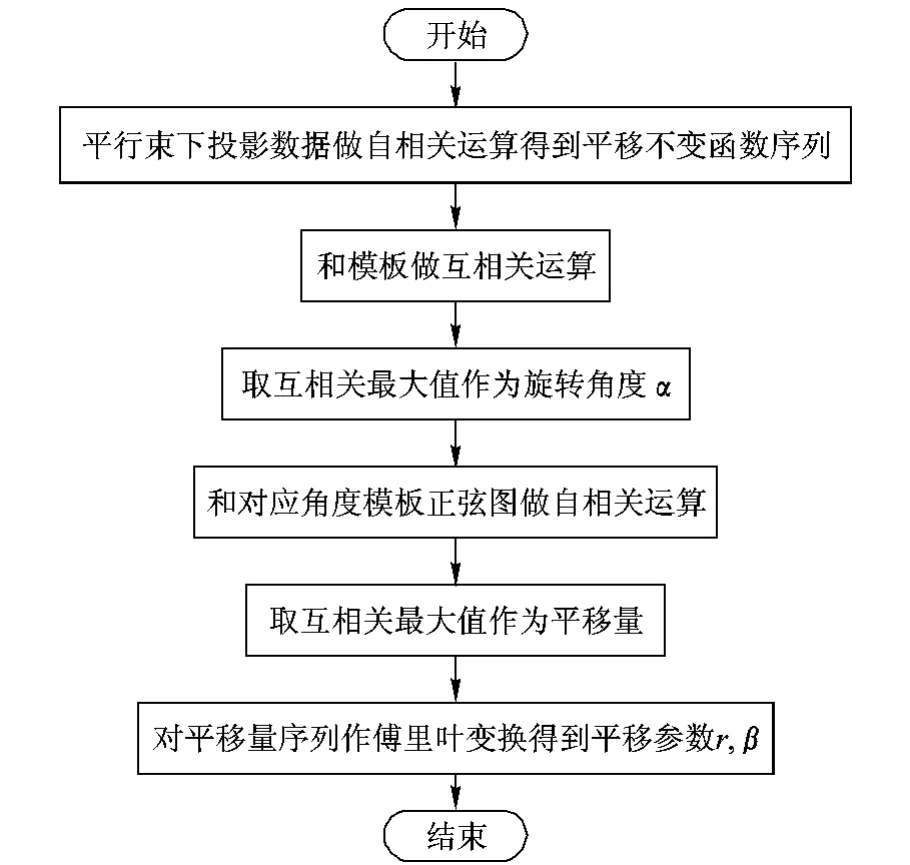
图3 正弦图的相关运算流程图

3 实验结果

本文对图 4所示的某一封装零件进行计算机断层扫描以判断该封装零件中是否存在多余物.该零件是密封的,内部结构不可见,因此实验中同时提供了一个确定不含任何多余物的标准件作为参考模板,将测试件的断层图像与标准件的同层断层图像相减,判断测试件中是否存在多余物.

图4 测试件与标准件的实物图

采集标准件和测试件的相同断层处(图 4中黑色直线所示)的 720幅投影数据,射线源到探测器的距离为 1100mm,采集到的正弦图如图 5、图 6所示.采用 R L滤波重建,重建图像如图 7、图 8所示.事实上测试件这一层并不存在多余物,图 7、图 8的特征理论上应该是一致的.但是由于测试件与标准件都是密封的,并不清楚其内部结构,再加上没有专用夹具,两次扫描两个工件在转台上的放置方位没有办法保持完全一致,因此图7和图 8中图像的特征出现了位置变化.

采用传统的 Fourier-Mellin配准算法对测试件的断层图像(图 8)和模版的断层图像(图 7)进行配准,配准后的图像如图 9所示.配准后图像的残差高达 76.6%,从图 9中也可以看出相同的特征并没有得到匹配.这是由于封闭件内存在着弹簧、电线等密度较大的物质,散射、硬化现象严重,在断层图像中存在严重的伪影,Fourier-Mellin算法估计参数时,难以准确地收敛到全局极值,所以配准的结果并不准确.

图5 标准件在断层处采集的正弦图

图6 测试件在断层处采集的正弦图

图7 标准件的断层图像

图8 测试件的断层图像

采用本文提出的基于正弦图的配准方法进行配准后的图像如图 10所示,配准后的残差只有7.87%,从图 10中也可以看出相同的特征很好地匹配在了一起.采用两种方法计算所得的变换参数如表 1所示.

图9 采用Fourier-Mellin算法配准后的图像

图10 采用本文提出的算法配准后的图像

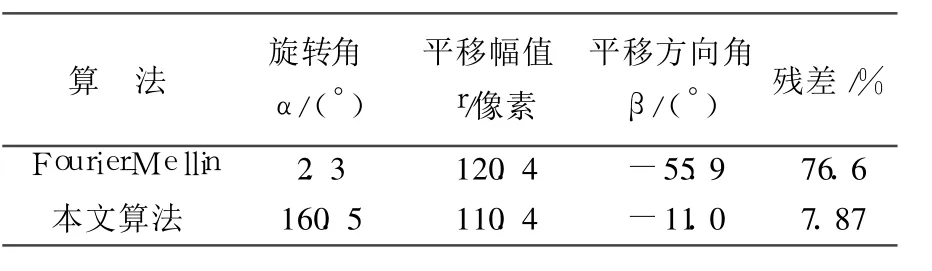
表 1 两种配准算法计算的变换参数

表 1可见,本文提出的基于正弦图的 CT图像配准方法,由于是在投影域内进行的,因此即使重建图像中存在严重的伪影,基于图像域的传统配准算法已经失效的情况下,也能估计出较为准确的变换参数,使特征得到较好的匹配.

4 结 论

通过理论分析与实验验证,本文提出的基于正弦图的 CT图像配准方法具有以下特点:

1)当重建图像中存在严重的伪影时,基于图像的配准算法已经失效,该算法依然取得了较好的配准效果,配准后图像残差仅为 7.87%;

2)本文提出的算法是利用平移后的自相关序列的残差最小来寻找旋转角度的,精度以投影采集的步进角为单位,如果在精度要求较高的情况下,可以通过对投影进行内插减小这一误差.

References)

[1]Maintz JB A,Viergeveramax A.A survey of medical image registration[J].Medical Image Analysis,1998,2(1):1-36

[2]Mark J,Peter B,Michael B,et al.Improved optimization for the robust and accurate linear registration and motion correction of brain images[J].Neuro Image,2002,17(2):825-841

[3]Guo Xiaoxin,Xu Zhiwen.An application of Fourier-Mellin transform in image registration[C]//Proceedings of the Fifth International Conference on Computer and Information Technology.Washington DC:IEEE Computer Society,2005:619-623

[4]Yang Z,Cohen F S.Image registration and object recognition using affine invariants and convex hulls[J].IEEE Transition on Image Processing,1999(8):934-946

[5]Foroosh H,Zerubia JB,Berthod M.Extension of phase correlation to subpixel registration[J].IEEE Transition on Image Processing,2002(11):188-200

[6]Alhichri H S,Kamel M.Virtual circ les:A new set of feature for fast image registration[J].Pattern Recognition Letters,2003(4):1181-1190

[7]陈灵娜,盛利元,陈俊熹.CT图像配准算法的研究与实现[J].医疗设备信息,2004,19(8):32-35 Chen Lingna,Sheng Liyuan,Chen Junxi.Research on CT image registration algorithm and its implementation[J].Information on Medical Equipment,2004,19(8):32-35(in Chinese)

[8]Reddy B S,Chatterji B N.An FFT-based technique for translation,rotation,and scale-invariant image registration[J].IEEE Transition on Image Processing,1996,5(8):1266-1271

[9]MaoWeihua,Li Tianfang,Wink Nicole.CT image registration in sinogram space[J].Medical Physics,2007,34(9):3596-3602

[10]Cain S C,Hayat M M,Armstrong E E.Projection-based image registration in the presence of fixed-pattern noise[J].IEEE Transitions on Image Processing,2001(10):1860-1872

[11]Lanzavecchia S,Tosoni L,Bellon P L.Fast sinogram computation and sonogram-based alignment of images[J].Oxford Journals,1996(12):531-537

[12]李保磊,傅健,黄巧珍,等.基于正弦图的工业 CT系统转台旋转中心的自动确定方法[J].航空学报,2009,30(7):1341-1345 Li Baolei,Fu Jian,Huang Qiaozhen,et al.Method for automatic determination of center of rotation in industrial computed tomography systemsbased on sinogram[J].Acta Aeronautica EtAstronautica Sinica,2009,30(7):1341-1345(in Chinese)

(编 辑:文丽芳)

Computerized tomography image registration based on sinogram

Sun Jingjing Yang Min Liu Jinghua Wu Wenjin

(School of Mechanical Engineering and Automation,Beijing University of Aeronautics and Astronautics,Beijing 100191,China)

In order to resolve the image registration problem in X-ray nondestructive testing,a new computerized tomography image registration algorithm based the mathematical relationship between the parts displacement and the change of the projection data was proposed.The algorithm preprocesses the projection data considering the practical computed tomography system,and utilizes the correlation between the projection data to search for the parts displacement.The algorithm can deal with registration problem of the two dimensional rigid transformation in the parallel and fan beam geometry.Because the proposed algorithm is done in the projection field before image reconstruction,it is more adaptive comparing with the conventional registration algorithms in the image field.Especially when the projection quality is low,there ism is sing projection and high level noise and there are severe artifacts in the reconstructed images,the proposed algorithm is more effective and reliable.The registration results of a sealed apparatus verify the performance of the algorithm.

computerized tomography;image registration;projection

TP 391.41

A

1001-5965(2011)02-0223-04

2009-12-30

国家自然科学基金资助项目(60872080);航天科技创新基金资助项目(CASC 0410);北京市科技新星基金资助项目(2005A 14)

孙晶晶(1982-),女,新疆哈密人,博士生,jinger0925@126.com.