基于光流信息的圆弧偏置比例导引规律

覃 天 陈万春

(北京航空航天大学 宇航学院,北京 100191)

邢晓岚

(空军装备研究院总体所,北京 100085)

基于光流信息的圆弧偏置比例导引规律

覃 天 陈万春

(北京航空航天大学 宇航学院,北京 100191)

邢晓岚

(空军装备研究院总体所,北京 100085)

提出了一种改进的用于被动寻的导弹的基于光流带落角约束的导引规律,其具有更强的适应性和更小的落角误差,而且该导引律不要求弹目距离信息,克服了被动寻的导弹不能测距的约束.基于采用光学传感器和光流算法的测量模型,受昆虫导航的启发,利用光流信息进行被动寻的导弹的导引和控制.同时借鉴偏置比例导引律的结构,重新设计偏置项,实现导弹以期望的落角命中目标.仿真表明,拦截地面运动目标时,该导引律在保证小脱靶量的同时,基本达到期望的落角,对于测量噪声也具有较好的鲁棒性.

光流;导弹;导引

在连续变动的图像平面中,探测器与环境间的相对速度会造成各个图像像素的运动,此种图像的运动速度即称之为光流.自然界中,光流被许多生物所应用.研究表明,苍蝇、蜜蜂、蜻蜓等的导航主要依赖于光流[1].在军事上,利用光流技术,不但可以快速准确地检测出复杂背景中的运动目标[2-3],而且光流场中包含的丰富的相对运动信息对于制导问题也很有用.

采用光学成像传感器(如相机)作为导引头,当目标进入导引头视场后,通过光流算法[2,4],可得到包含目标在内的光流场.由于目标光流反映了导弹加速度的变化,因此,可以利用目标的光流信息来导引导弹完成对目标的拦截,再利用目标在导引头视场中的位置信息实现导弹落角约束的要求.

按此原理,文献[5]提出了基于光流信息的新的 CNG(Circle Navigation Guidance)导引方法,对固定目标,可获得零脱靶量和零落角误差的效果,但对运动目标却存在较大的落角误差.

针对运动目标,本文进一步提出了基于光流信息的圆弧偏置比例导引方法,利用偏置比例导引思想[6]考虑落角约束要求,并重新设计偏置项,有效解决了运动目标落角误差大的问题.

本文不考虑导弹的模型误差和气动阻力等问题,导弹和目标均假设为以恒定速率在三维空间中运动的质点.另外,本文不对光流算法问题进行讨论,而假设目标光流是可得到的.

1 问题简介

本文要解决的问题是如何导引导弹在三维空间中沿着期望的弹道以一定的角度击中目标.考虑一个简单的弹目模型,如图 1所示.XR为导弹目标的相对位置矢量;VM为导弹速度;VT为目标速度;aT和 aC为分别为目标和导弹的加速度,并且

由于有落角要求,所以定义一个最终的期望速度矢量 VF,如图 1所示.θT为目标航向角,γ为落角,逆时针为正,则 VF的方向可表达为

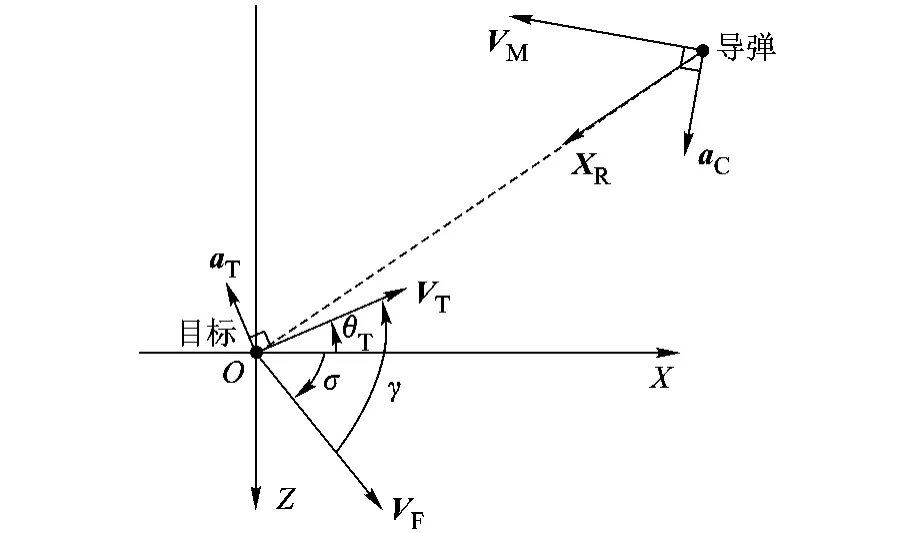
图1 弹目模型

该模型下,问题就表述为找到一个控制信号aC,使导弹在某个时刻 T同时满足下面两个状态:

导弹可用的导引信息有:导弹视场中目标的光学位置,目标光流,导弹最终期望速度,导弹当前速度和加速度以及导引头框架角等.

2 光流中的有效导引信息

光流中包含丰富的运动信息,但目标光流并不能直接用于导弹的导引,需要提取当中的有效导引信息,这需要建立起光流与目标运动的关系.

摄像机模型(简化的导引头模型)如图 2所示,设在时刻 t,视场内目标点 P(X,Y,Z)在成像平面上的对应点为 p(x,y).设摄像机坐标系中 3个坐标轴的单位矢量分别为那么 p点在摄像机坐标系中的位置矢量可以表示为

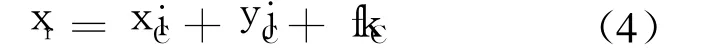
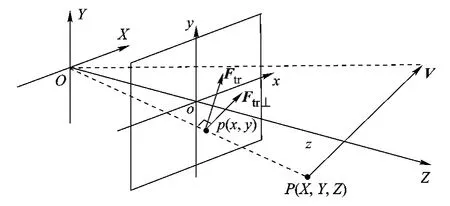
图2 光流中的导引信息

由于光流由摄像机和目标相对的平移运动和旋转运动产生,因此,光流 F可分解为平移分量Ftr和旋转分量 Frot.

式中,目标光流 F由摄像机提供的目标图像序列经过光流算法得到,Frot由摄像机和目标间的相对转动引起.该相对转动可分解为弹体的转动和摄像机框架的转动,这些转动信息都可通过弹上陀螺和框架上的传感器得到.

图2中,V为 P点的相对速度;Ftr为由 V引起的光流平移分量;Ftr⊥是 Ftr在视线(即沿 OP的方向)垂直方向上的投影分量,是本文制导律中光流控制分量需要的主要信息.

3 光流导引律

定义一个当前期望速度矢量 VD(区别于最终期望速度矢量 VF),见图 3,它和 VF关于目标视线(LOS,Line of Sight)对称,eλ为 VM与 VD之间的夹角,λ和 ε分别为 VM,VF与 LOS的夹角.

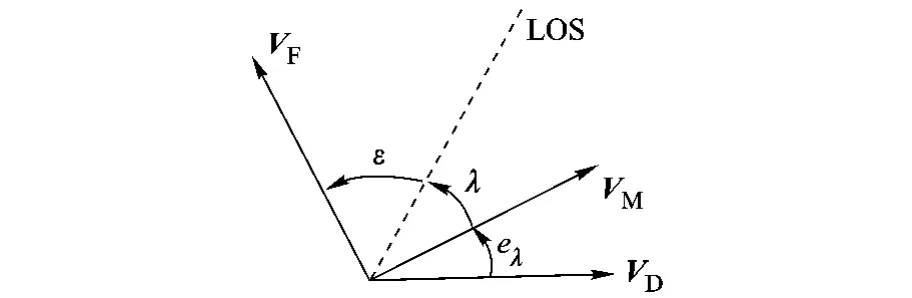
图3 当前期望速度与最终期望速度的关系

考虑二维平面内的情况,假设目标固定,若能保证 λ和 ε在任何时刻都严格相等,即 VM与 VD一致,那么导弹会沿一个唯一确定的圆弧弹道飞行,并以期望的落角击中目标,如图 4所示(V′F是 VF的平移矢量).这就是 CNG方法的主要思想,根据文献[5],CNG导引律表达式为

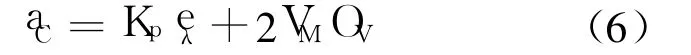
式中,aC为指令加速度;Kp为比例增益;Ov为相对速度引起的目标光流.等号右边的第 1项使导弹逼近圆弧形弹道,第 2项使导弹稳定在圆弧形弹道上.

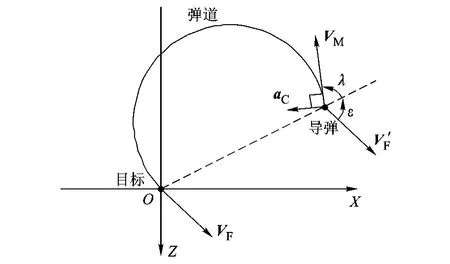
图4 CNG导引律弹道示意图

CNG导引律在固定目标的情况下,可以同时达到零脱靶量和最终期望落角,但对于运动目标,则有较大的落角误差.为了解决这一问题,参考偏置比例导引方法(BPN,Biased Proportional Navigation)[6]的基本思想后,通过重新设计偏置项来减小最终的落角误差.

BPN由纯比例导引律加上一个时变的偏置项组成.其中比例导引项的作用是通过零化视线角速率来零化导弹速度方向和目标视线方向之间的偏差,时变的偏置项的作用是零化目标视线和期望碰撞方向之间的偏差.该导引律的目标就是同时零化速度方向偏差和目标视线偏差.根据这一思想,本文将重新设计式(6)中等号右边的第 1项.将输入的光学位置误差信号 eλ重新定义为目标视线与 VD之间的夹角,另记为 eδ.下面定义一个单位矢量 u1:

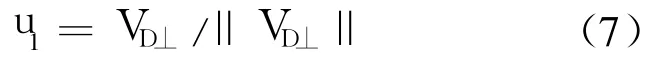
式中,VD⊥是 VD垂直于目标视线的分量在 VM垂直方向上的投影.则导引律中新的光学位置控制分量 up可以表达为

由图 2可知,光流大小和目标相对速度的大小、目标相对速度与目标视线的夹角等都有密切关系.因此,可将目标光流作为第 3个控制分量的输入信号,并将与光流相关的输入信号记为 OF.同时定义单位矢量 u2:

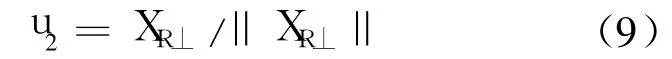
式中,XR⊥是XR在 VM垂直方向上的投影.则导引律中新的光流控制分量 uf可以表达为

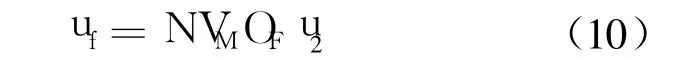
式中 N为常数.新的光流导引律为

式(12)中,VMR为 VM在目标视线方向上的投影,K为常数.

下面为参数 Kp,N以及光流信号 OF的取值.

4 仿真结果

本部分以导弹打击地面运动目标(比如坦克、装甲车辆等)为例,采用本文提出的导引方法(OF-CBPNG,Optical Flow-Circle Biased Proportional Navigation Guidance)进行了仿真,并与 CNG导引律和带落角约束的偏置比例导引律 BPNG[6]的仿真结果作对比.仿真的终止条件为弹目距离小于 0.1m,落角约束为要求导弹垂直向下命中目标.K取 0.125,N取 3,仿真初始条件见表 1.

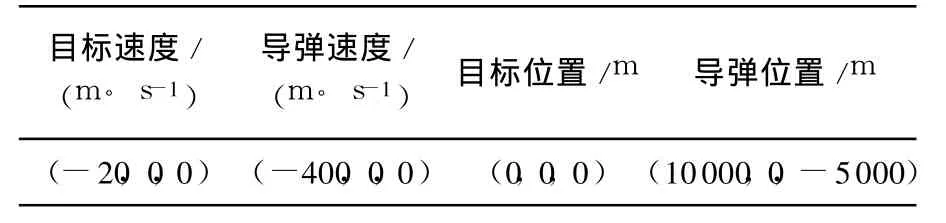
表 1 仿真初始条件

按照表 1给出的初始条件进行仿真,分别得到了 3种导引律的弹道曲线、导弹加速度和落角误差(见图 5、图 6和表 2).

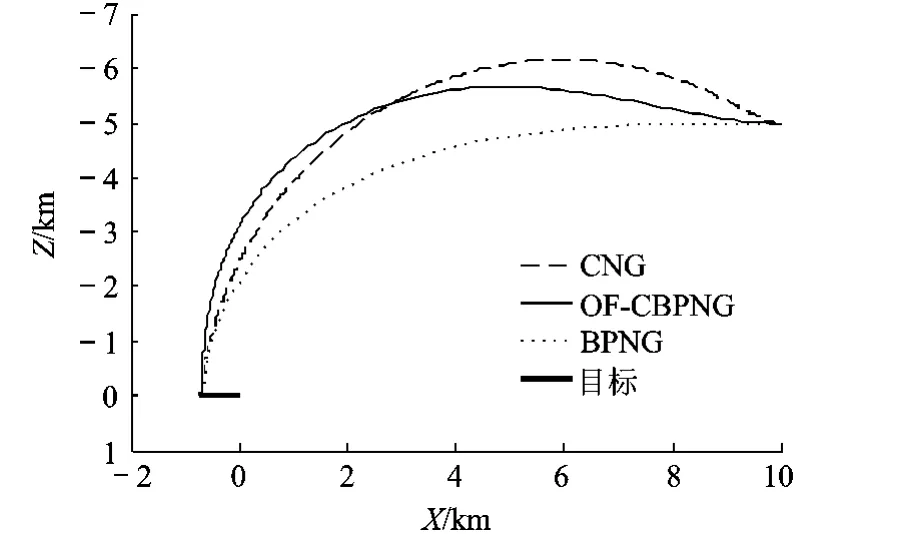
图5 3种导引律的弹道对比

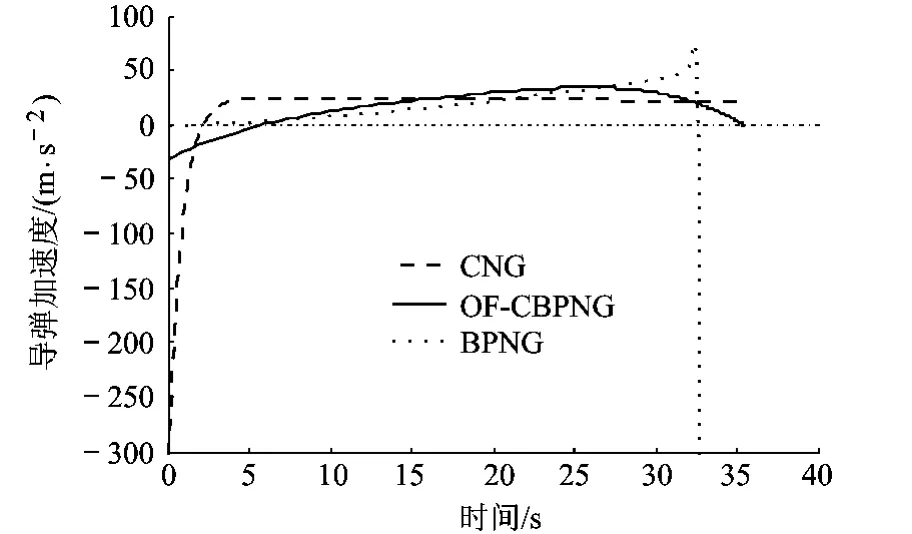
图6 3种导引律的加速度对比

表 2 3种导引律的落角误差

3种导引律相比,CNG的落角误差最大,而OF-CBPNG将误差角减小了 1/2左右,BPNG能准确达到期望的落角,但在拦截末段的需用过载急剧增加,若对可用过载进行限制,则 BPNG会产生较大的脱靶量.此外,BPNG还额外需要弹目距离作为导引信息,而 CNG和 OF-CBPNG则不需要.

从整个拦截过程来看,OF-CBPNG的需用过载都较小,而且变化平稳.在最后接近目标的过程中,由于 OF-CBPNG需用过载趋近于 0,导弹攻角会逐渐趋近于 0,而 OF-CBPNG产生的落角误差也较 CNG方法小许多,使导弹能产生更好的杀伤效果.另外,在拦截初段,CNG导引律使导弹速度迅速向上方偏转,导致导弹速度与视线间的夹角也迅速增大,从而增加了导引头碰框的危险.

图7为 OF-CBPNG仿真中,接近目标时导弹视场的变化.该图表明,越接近目标,导弹与目标在垂直视线方向上的相对运动越小,因此目标光流也越小.

图7 拦截中段和末段的目标光流示意图

图8为光学位置测量噪声为 0.01 rad2,光流测量噪声为 0.001 rad2/s2时各种落角约束下产生的落角误差.由图可知,在大部分的落角约束条件下,OF-CBPNG的落角误差要比 CNG的小.

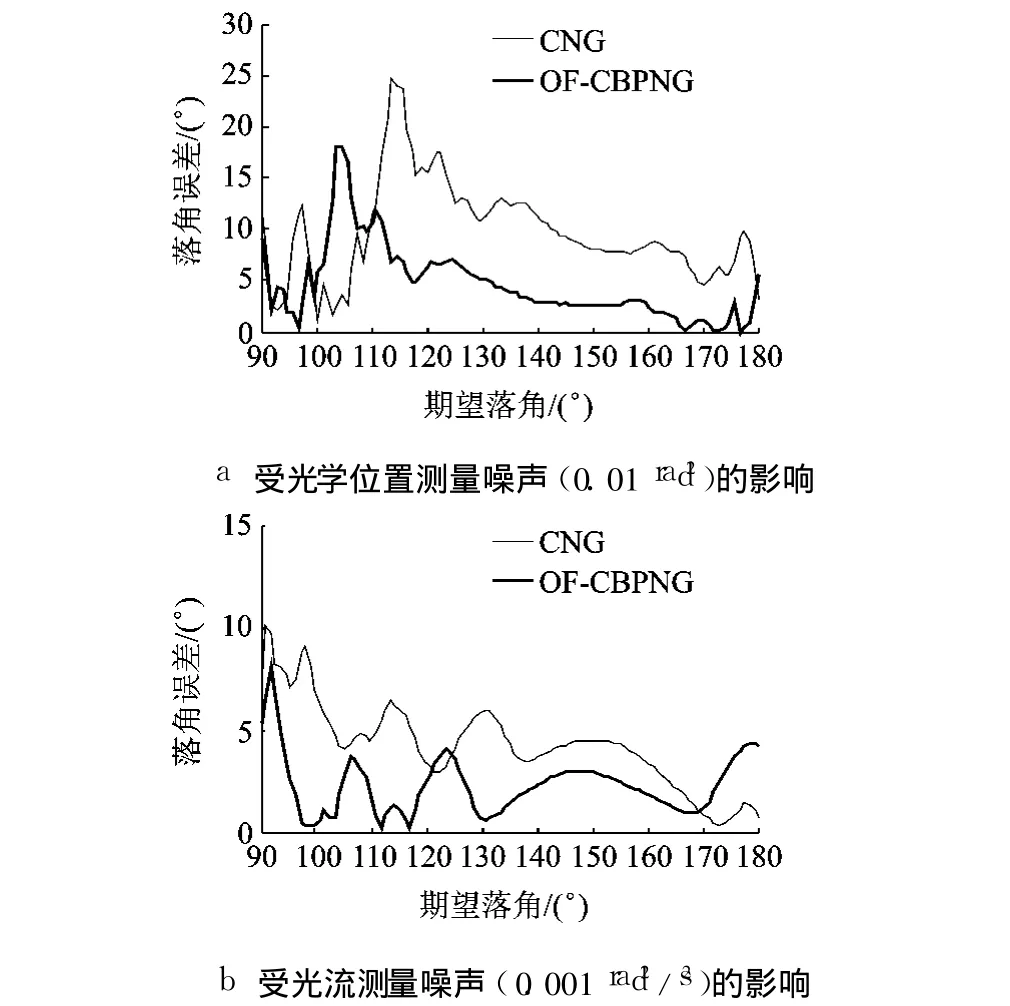
图8 有测量噪声时不同落角约束下的落角误差

5 结束语

本文以 CNG方法为基础,以光流作为主要的导引信息,提出了一种新的导引方法 OF-CBPNG.本方法针对运动目标,在满足脱靶量要求的前提下,能明显减小 CNG方法的落角误差,对测量噪声也具有更好的鲁棒性.另外,与 BPNG方法相比,本方法的需用过载小得多,最突出的优点是不需要弹目距离信息,便于在被动寻的导弹上实现.

References)

[1]Srinivasan M,Zhang S,Lehrer M,et al,Honeybee navigation en route to the goal:visual flight control and odometry[J].The Journal of Experimental Biology,1996,199(1):237-244

[2]李平岐,陈万春,邢晓岚.复杂背景下运动目标的检测与跟踪[J].红外与激光工程,2007,36(增刊 2):182-186 Li Pingqi,Chen Wanchun,Xing Xiaolan.Detection and tracking ofmoving object in complex background[J].Infrared and Laser Engineering,2007,36(Supplement 2):182-186(in Chinese)

[3]Thompson W B,Pong TC.Detecting moving object[J].International Journal of Computer Vision,1990,4(1):39-57

[4]Srinivasan M V.An image-interpolation technique for the computation of optic flow and egomotion[J].Biological Cybernetics,1994,71(5):401-415

[5]Manchester IR,Savkin A V,Faruqi F A.Optical-flow based precision missile guidance inspired by honeybee navigation[C]//Proceedings of the 42nd IEEE Conference on Decision and Control.Hawaii:IEEE,2003:5444-5449

[6]Kim B S,Lee G L,Han H S.Biased PNG law for impact with angular constraint[J].IEEE Transactions on Aerospace and Electronic Systems,1998,34(1):277-288

(编 辑 :李 晶)

Op tical-flow based circle biased proportionalnavigation

Qin Tian Chen Wanchun

(School ofAstronautics,Beijing University of Aeronautics and Astronautics,Beijing 100191,China)

Xing Xiaolan

(Airforce Equipment Research Academy,Beijing 100085,China)

For the passive homing missiles,a developed guidance law based on optical flow was proposed to impact amoving target with an impact angle constraint.In contrast to optical-flow based circle navigation guidance,it is more practical and precise.Meanwhile the improved one does not require the range information,which avoids the problem that the range information can not be measured directly by a passive homing seeker.Based on ameasurement modelusing an optical sensor and optical flow calculation and inspired by the insect navigation,the optical flow was used in guidance and control for a passive homing missile.Employing the structure of biased proportional navigation,the bias term was redesigned to ensure the impact angle.The simulation results show that,a smallmiss distance and a desired impactangle are obtained when the new guidance law is used to impact a moving ground target,also this guidance law is much robust to measurement noise.

optical flows;missiles;navigation

TJ 765

A

1001-5965(2011)02-0189-04

2009-12-15

覃 天(1982-),男,广西河池人,博士生,qintian@sa.buaa.edu.cn.