基于 RBF网络的导弹滑模动态逆控制律设计

杨志峰 雷虎民 李庆良 李 炯

(空军工程大学 导弹学院,三原 713800)

基于 RBF网络的导弹滑模动态逆控制律设计

杨志峰 雷虎民 李庆良 李 炯

(空军工程大学 导弹学院,三原 713800)

讨论了一种基于径向基函数(RBF,Radial Basic Function)神经网络的导弹滑模动态逆控制律.导弹的基本控制律采用动态逆方法设计,对慢回路设计神经网络滑模控制器以补偿整个控制系统的不确定性.即用 RBF神经网络逼近导弹慢模态不确定性的数学模型,并将逼近误差引入到网络权值的调节律以改善系统的动态性能;滑模控制器用于减弱模型不确定性及神经网络的逼近误差对跟踪的影响.所设计的控制器不仅保证了闭环系统的稳定性,而且使模型不确定性及神经网络的逼近误差对跟踪的影响减小到给定的性能指标.最后通过仿真分析,验证了该方法的有效性.

导弹;动态逆控制;神经网络;滑模控制

动态逆控制方法已成功应用于飞行器控制系统的设计中.但该方法所设计控制器鲁棒性无法保证[1-2].近年来,神经网络在不确定非线性系统的鲁棒控制中已得到了大量研究[3-4],其控制器可保证系统鲁棒镇定.滑模控制也是非线性系统控制经常采用的一种控制方法[4-5],其控制器具有较强鲁棒性,同时设计简单且易于实现.因而将动态逆、神经网络和滑模控制相结合应用于飞行器控制器的设计之中,使控制器不仅能保证系统鲁棒镇定而且具有一定的鲁棒指标,具有很强的现实意义.

本文结合 RBF(Radial Basic Function)神经网络、动态逆控制以及滑模控制,针对导弹非线性系统,设计了一种新的控制律.首先基于动态逆方法设计导弹的快慢回路控制器,然后将存在模型不确定性的导弹慢回路的非线性函数分解成已知部分和未知部分,将未知部分用 RBF网络进行逼近,进而引入一种滑模控制器.用来减小系统的跟踪误差,起鲁棒控制作用.仿真研究表明了所设计的控制律的有效性.

1 导弹的双阶段动态逆控制

1.1 导弹非线性动态模型

本文考虑导弹非线性控制模型如下:

式中

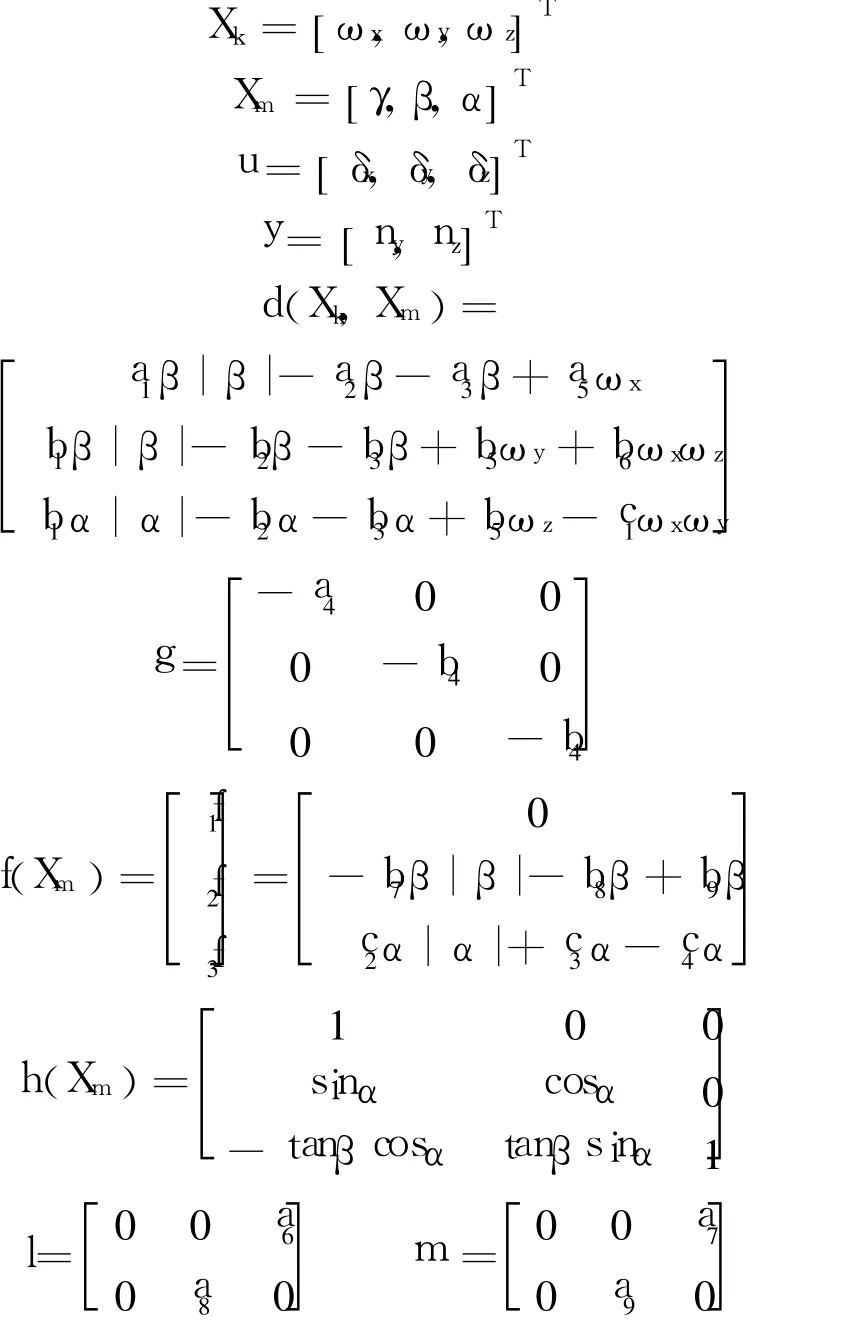
其中,Xk和 Xm分别表示导弹快和较慢状态;ai,bj和 cj(i=1～9,j=1～4)分别为滚转、偏航和俯仰通道的气动导数;ωx,ωy,ωz分别为滚转、偏航和俯仰角速度;γ,β,α分别代表滚转角、侧滑角和攻角 ;δx,δy,δz分别为副翼 、方向舵和升降舵的偏转角;ny,nz分别为导弹的纵向和侧向过载.

1.2 基于动态逆的导弹控制律设计

根据时标分离原理,状态 Xk响应较快常被定义为快模态,而状态 Xm响应较慢定义为慢模态[1].

式 (1)中 ,因 a4,b4不为 0,且 α∈ [0,π/2),故 g,h(Xm)均为可逆阵.

快回路控制器设计:

设指令输入为 Xkc=[ωxc,ωyc,ωzc]T,设计快回路预期动态为

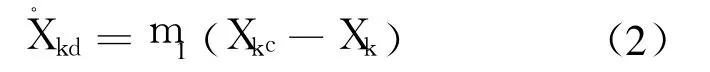
其中,m1≥0.将式(2)代入式(1)可求得快回路的控制输入:

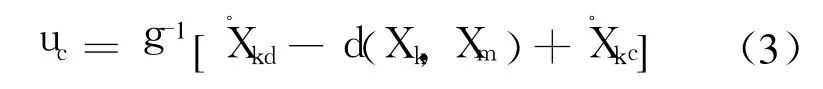
慢回路控制器设计:

指令输入为 Xmc=[0,βc,αc]T,设计慢回路预期动态为

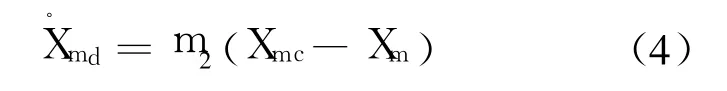
其中,m2≥0,则由式(1)可求得慢回路的控制输入:

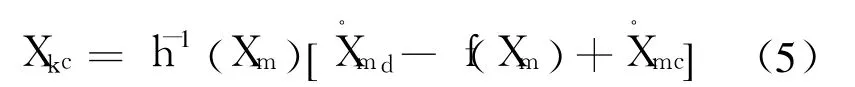
式 (1)中 α7≪α6,α9≪α8,故可忽略后面一项,进而通过过载指令 ny,nz和滚动角指令 γc=0,得到期望的慢回路输入指令 Xmc.

由文献[6]对时标分离系统的逆控制进行的研究可知:系统中存在的不确定性的主要原因是由于慢回路中存在动态逆误差,因此通过对慢回路进行鲁棒控制律设计,可保证整个系统的鲁棒性.

2 基于 RBF网络的慢回路滑模控制

2.1 控制律设计

给出慢回路的状态方程另一种形式为

式中,f(·)和 h(·)为标称函数,即已知部分;Δf(·)和 Δh(·)为的参数摄动引起的不确定性,且 Δf和 Δh有界;d(·)包括外界扰动及快回路反映到慢回路的逆误差,且‖d‖2≤D有界;u=Xk∈R3和 y∈R3分别为系统的输入和输出;状态 Xm∈R3慢模态状态量,对于给定的参考信号 ym=Xmc,定义跟踪误差 e=ym-y.

其中,wf,wh为相应的网络权值矩阵;Φf和 Φh为网络的基函数矩阵.

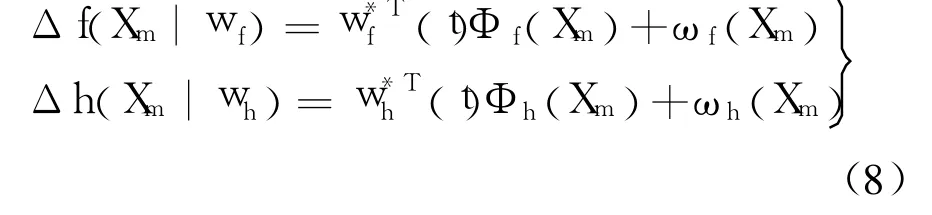
其中,ωf(Xm)和 ωh(Xm)为神经网络的最小逼近误差,现假设

Wf(Xm)＞0,Wh(Xm)＞0为网络逼近误差的上界.

设计如下形式的控制器:

式中

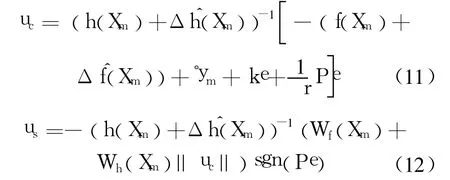
其中,k=m2＞0,r＞0为设计参数;P=PT＞0是如下 Riccati方程的解.

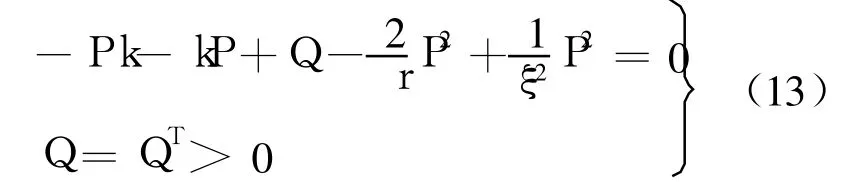
uc为系统的等效动态逆控制器;us为系统的滑模控制器,起鲁棒控制作用,且滑模控制器的滑模面选为S=e.

设计 RBF网络的权值调节律为

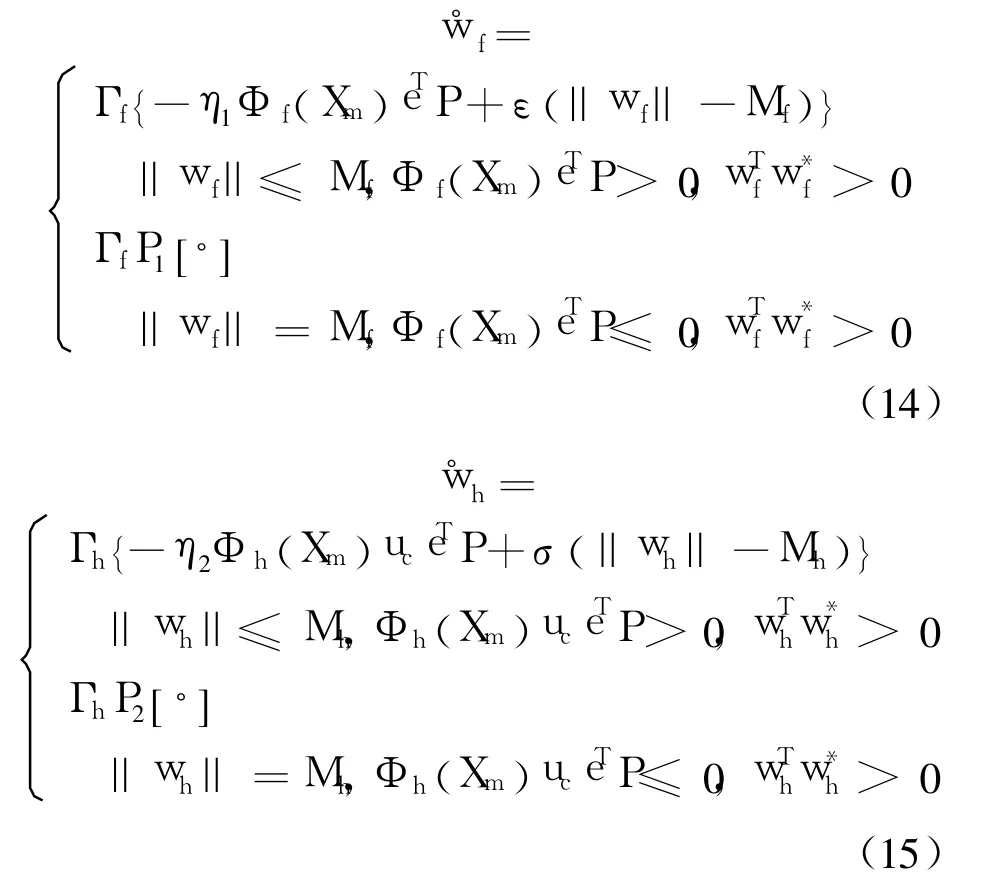
其中,η1和 η2为神经网络学习率 ;Γf,Γh为正定对称的加权矩阵;Mf,Mh为设计参数;ε=λ1sgn(wf);σ=λ2sgn(wh);λ1,λ2为大于 0的常数.投影算子的定义为

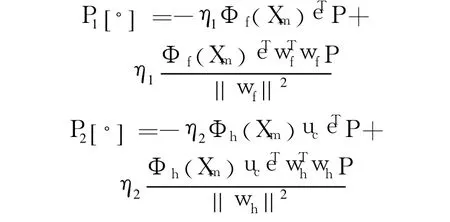
2.2 稳定性分析

根据文献[4,6],最终可证明由式(6)所表示的导弹慢回路,在控制量为式(10)及网络权值 wf和 wh的调节律为式(14)和式(15)的情况下,有:

1)在控制器为式(10)的作用下,跟踪误差小于给定的性能指标为式(16),且系统稳定能达到期望的跟踪效果,同时系统滑模条件成立.

2)‖ wf‖≤Mf,‖wh‖ ≤Mh,Xm,u∈ L∞.

3 仿真分析

为验证所设计基于神经网络的滑模动态逆控制律的有效性,对导弹控制系统的性能进行仿真和分析.模型中的力和力矩的气动系数均做 30%的摄动处理,得到新的参数作为导弹的真实模型.取快回路的 m1=30,慢回路的 m2=k=6,使其相差3～5倍.分别对单纯采用动态逆控制和引入神经网络的滑模动态逆控制进行仿真比较,结果如图 1～图 3所示.

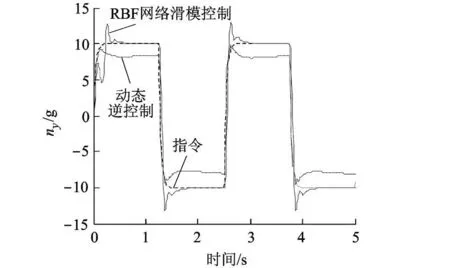
图1 纵向过载ny的曲线

由图 1和图 2可知,在跟踪指令信号的情况下,动态逆控制方法对导弹参数摄动较为敏感,系统产生了较大的稳态误差,纵向过载的表现尤为明显;而在引入神经网络滑模控制后,其鲁棒性明显增强,控制效果明显好于单纯的动态逆控制系统;由图 3可知导弹滚动角在初始值为 5的情况下,能迅速响应恢复至 0,鲁棒性受参数摄动影响较小.

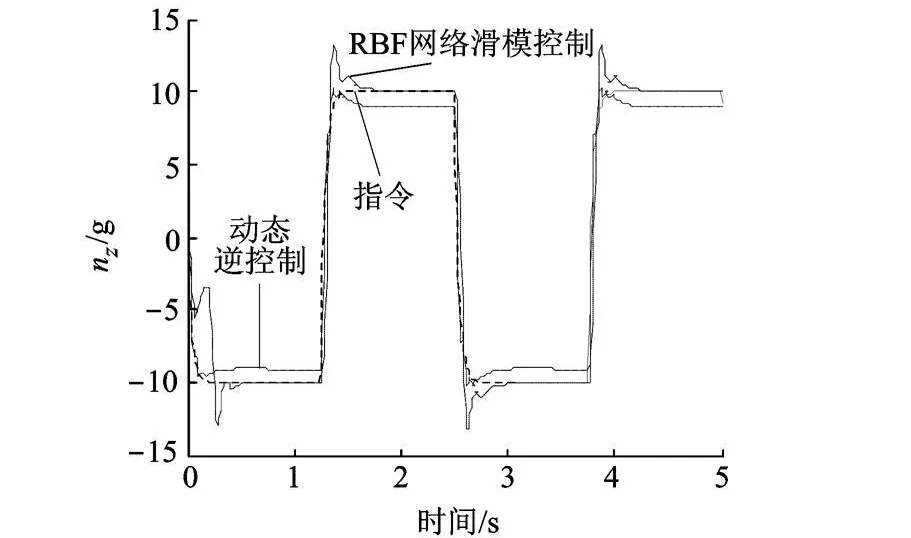
图2 侧向过载 nz的曲线

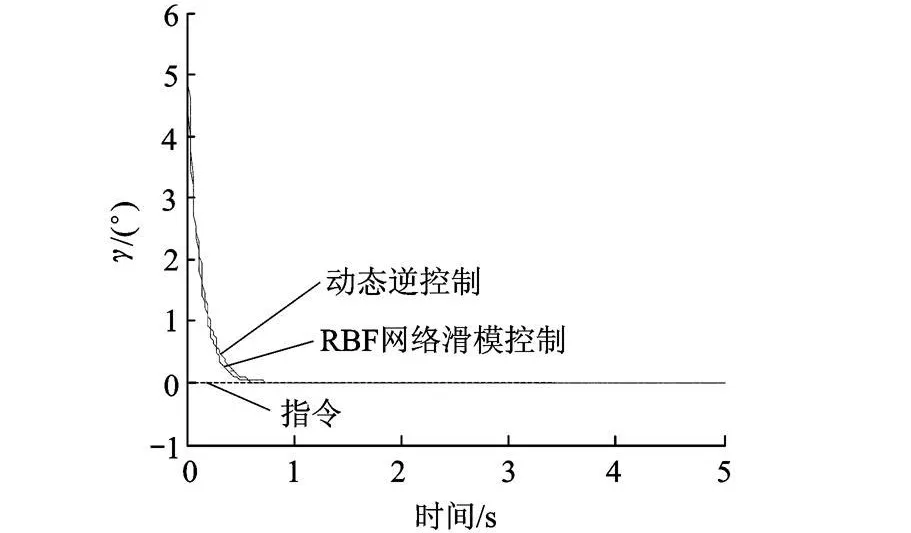
图3 滚转角 γ的曲线

4 结束语

本文首先对非线性导弹的快、慢模态分别设计了动态逆控制律,然后对存在有动态逆误差的慢模态设计了神经网络滑模控制律,同时将神经网络的逼近误差引入到网络权值的调节律中,加快了逼近速度,从而改变了系统的动态性能和鲁棒性能.仿真结果验证了该方案的有效性和可行性.

References)

[1]曾宪法,张磊,申功璋.基于动态逆和分散控制的导弹控制系统设计[J].北京航空航天大学学报,2007,33(11):1303-1307 Zeng Xianfa,Zhang Lei,Shen Gongzhang.Design of control system for missiles based on dynamic inversion and decentralized control[J].Journal of Beijing University of Aeronautics and Astronautics,2007,33(11):1303-1307(in Chinese)

[2]张艳,段朝阳,张平,等.基于动态逆的 BTT导弹自动驾驶仪设计[J].北京航空航天大学学报,2007,33(4):422-426 Zhang Yan,Duan Chaoyang,Zhang Ping,elal.BT Tmissile autopilot design based on dynamic inverseion[J].Journal of Beijing University of Aeronautics and Astronautics,2007,33(4):422-426(in Chinese)

[3]Chen Chiu-Hsiung,Lin Chih Min,Te Yu Chen.Intelligent adaptive control for MIMO uncertain nonlinear systems[J].Expert Systems with Applications,2008,35(3):865-877

[4]陈谋,姜长生.基于神经网络的一类非线性系统自适应滑模控制[J].应用科学学报,2004,22(1):76-80 Chen Mou,Jiang Chang sheng.Adaptive sliding model control for a class of nonliear system based on neural networks[J].Journal of Applied Sciences,2004,22(1):76-80(in Chinese)

[5]Laghrouche S,Smaoui M,Plestan F,et al.Higher order sliding mode control based on optimal approach of an electro pneumatic actuator[J].International Journal of Control,2006,79(2):119-131

[6]姜长生,王从庆,魏海坤,等.智能控制与应用[M].北京:科学出版社,2007:354-409 Jiang Changsheng,Wang Congqing,Wei Haikun,et al.Intelligent control and application[M].Beijing:Science Press,2007:354-409(in Chinese)

(编 辑:赵海容)

Design of sliding model and dynamic inverse control law for a missile based on RBF neural-networks

Yang Zhifeng LeiHumin Li Qingliang Li Jiong

(The Missile Institute,Air Force Engineering University,Sanyuan 713800,China)

A radialbasic function(RBF)neural networks based sliding model control and dynamic inverse control approach to a missile was presented.The basic control law was designed by dynamic inversion,and neural networks based sliding model and dynamic inverse controller was designed for the slow loop to compensate the uncertainty of the whole control system.The RBF neural networks were used to approximate the uncertainty of slow states model of missile and the approximation errors of the neural networks were introduced to the design of adaptive adjust law to improve the quality of the systems.Sliding model controller was used to attenuate the uncertainty of model and the approximation errors of the neural networks.The controller could guarantee stability of overall system and attenuate effect of uncertainty of model and approximation errors of neural networks to a prescribed level.Finally,simulation results show the effectiveness of the control method.

missile;dynam ic inverse control;neural networks;sliding model control

TP 391.9

A

1001-5965(2011)02-0167-04

2009-12-25

航空科学基金资助项目(20090196005)

杨志峰(1983-),男,山西大同人,博士生,laoyang11045@163.com.