基于经验模态分解的局部放电信号窄带周期干扰的抑制

勾建军，王振浩，薛雷

(东北电力大学电气工程学院，吉林吉林132012)

0 引言

局部放电在线检测是反映电力设备绝缘状况的重要手段之一，对维持电力系统稳定和安全的运行具有重要的意义。在绝缘缺陷的早期局部放电信号十分微弱［1］，而且，现场实际检测中，通常伴随有白噪声、窄带周期性干扰和脉冲型干扰，使得局部放电在时域波形中无法分辨，其中，窄带周期性干扰最为严重。所以，有效地将局部放电信号从窄带周期性干扰中提取出来，对分析电力设备绝缘状况就显得尤为重要［2］。

以往对窄带周期性干扰的抑制有多种信号处理方法:如FFT滤波、自适应滤波、小波分解阈值法等。FFT滤波方法适用于平稳信号，自适应性差，对于局部放电信号的处理效果并不理想。传统的基于LMS自适应滤波方法在处理多频率且频率范围宽的信号时，滤波器的参数选择存在很大困难。文献［3］以小波分解为预处理，较好地解决了滤波器参数的选择问题，但对于未知信号的小波基函数的选取仍较为困难。文献［4-5］以经验模态分解为预处理，回避了小波基函数选取的问题，而定步长的限制使得信号处理结果的收敛速度和稳定性不是十分理想。因此，提出以经验模态分解(Empirical Mode Decomposition，EMD)为基础，结合变步长自适应滤波的方法来对窄带周期性干扰进行处理，将含有多频率的窄带周期性干扰信号分解成含有少量频率的若干个固有模态函数(Intrinsic Mode Function，IMF)，再分别对各个IMF进行变步长自适应滤波，以改善传统方法在干扰抑制方面的不足。

1 经验模态分解原理

EMD方法适用于分析非线性、非平稳信号，具有很高的信噪比和分辨率［6-7］。该方法认为，任何复杂信号都是由局部调幅调频成分构成的，因此可由复杂的信号中直接分离出从高频到低频的若干阶基本函数，即IMF，从而突出了原信号的局部特征信息。IMF满足如下特点:a.其极值点和过零点的数目应该相等或至多差1;b.分别连接局部极大值和局部极小值所形成的2条包络线的均值在任一点处为零。

对于任意信号x(t)，EMD算法描述如下:

首先，确认出s(t)上所有极值点，然后将所有极大值点和所有极小值点分别用1条样条曲线连接起来，使2条曲线间包含所有的信号数据，从而得到s(t)的上下两条包络线。设2条包络线的平均值为m，s(t)与m的差值记作h，令h=s(t)-m，将h视为新的s(t);重复以上操作，直到h满足一定的条件，令c1=h，c1视为一个IMF，令r=s(t)-c1，将r视为新的s(t);重复以上过程，依次得到第2个IMF分量，第3个IMF分量，直到r满足给定的终止条件时筛选终止。由此可得s(t)的分解式为

式中r称为残余函数，反映了信号的平稳趋势。由式(1)可知，原始信号可以表示为n个IMF分量和一个残余项的和。在时域上，任何一个IMF表现为某一尺度范围的模式，体现良好的多尺度特性;在频域上，表现为从高频到低频的层层过滤，体现了良好的时空滤波特性。整个分解过程中没有能量损失，可以用分解得到的各个IMF分量和残余项来精确重构原始信号［8］。

2 基于EMD变步长自适应滤波算法

自适应滤波器以最小均方(LMS)自适应算法最为常用。图1为自适应滤波器的基本原理图［9］。

图1 自适应滤波器原理图

考虑到传统自适应滤波器步长为定值的限制，采用了一种简便的变步长自适应滤波方法，其权系数矩阵［9］为:

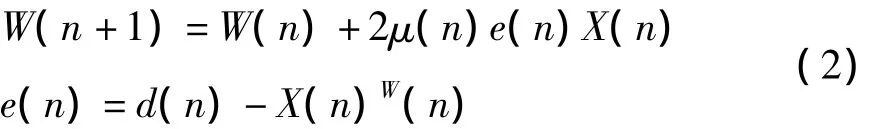
式中W(n)为n时刻自适应滤波器权系数;μ为步长因子，影响算法的稳定性和收敛速度;X(n)为n时刻输入信号;e(n)为误差信号。步长的更新式［10］为

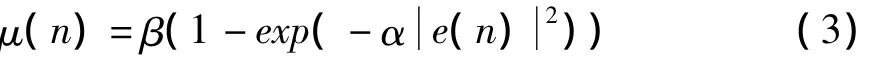
式中参数α(α＞0)用来控制函数的形状，参数β(β＞0)用来控制函数的取值范围，参数α、β根据初始误差的大小来进行选择。由式(3)可知，步长函数μ (n)可以很好的跟踪误差e(n)的变化，初始阶段e (n)较大时，μ取得较大值，加快收敛速度;而在较小时，取得较小值，具有较好的稳定性，保证其在滤波过程的各个阶段均能达到合适的步长，提高了自适应滤波器的性能。

采用的基于EMD的变步长自适应滤波方法具体操作步骤如下:

a.将混有窄带周期干扰的局部放电混合信号进行EMD分解，将多频率的干扰信号分散到各个IMF中，并根据残差的要求选择合适的分解层数。

b.针对各个IMF分量，设定参数α、β的值，利用干扰与局放信号延时后相关性的特点，对其分别进行变步长自适应滤波，保留相关性弱的局放信号。

c.将预处理后的各个IMF分量，从低频到高频进行重构，所得结果即为去噪后的局放信号。

3 仿真信号分析

局部放电脉冲的持续时间很短，只有几个μs，通常分成指数衰减模式和指数衰减振荡模式，放电脉冲频谱主要集中在10～50 MHz之间，所以电力电缆局部放电脉冲理论上可以用以下的数学模型来等效［3］:

a.单指数衰减形式

双指数衰减形式

以上两种模型虽然接近真实的放电波形，但一般传感器在实际工程中通常检测得到的是振荡信号，因此该局放脉冲又可用如下衰减振荡模型来等效［8］:

b.单指数衰减振荡形式

双指数衰减振荡形式

式中A为信号的幅值;τ为衰减系数;fc为振荡频率。

以衰减振荡形式的局部放电信号进行仿真，图2为局部放电的仿真信号。仿真信号取幅值A为1mV，振荡频率fc为1 MHz，采样频率为10 MHz。其中，1、3信号为单指数衰减振荡形式，衰减系数τ分别为1 μs和2 μs;2、4信号为双指数衰减振荡形式，衰减系数τ分别为1μs和2μs。

图2 局部放电仿真信号

仿真时选用的窄带周期性信号表达式为:

式中振幅A为0.2mV，干扰频率有7个主频率，分别为 120kHz、200kHz、350kHz、625kHz、1 200 kHz、1 800 kHz、2 500 kHz。叠加窄带干扰后的局部放电信号见图3。

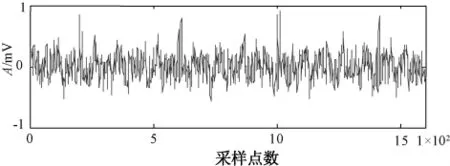
图3 叠加窄带干扰的局放信号

对图3叠加干扰后的局放信号进行EMD分解，根据残差的判断，选择分解到7层为宜，结果见图4。

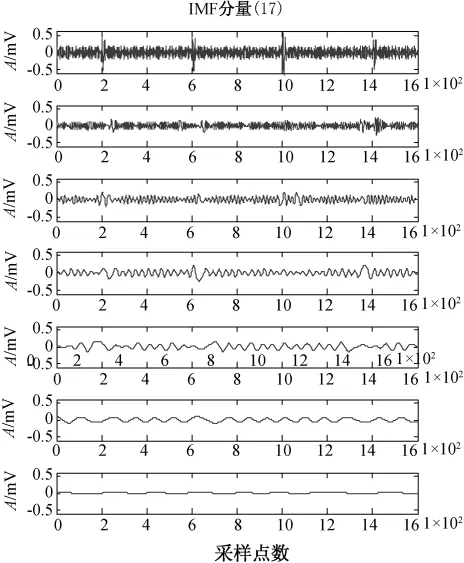
图4 信号的EMD

由图4可知，EMD分解是将信号从高频到低频分解成若干个IMF，而且信号中混有的多个频率同时也被分散到各个IMF当中，将分解后的每一个IMF进行变步长自适应滤波处理，α、β均取值0.98，最后将预处理后IMF从低频到高频进行重构，即为去噪后的结果，见图5。图6为EMD处理后通过定步长自适应滤波的处理结果。

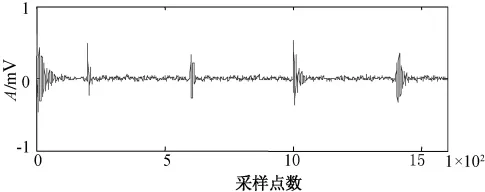
图5 变步长的处理结果

图6 定步长的处理结果

从图5与图6的比较可以看出，两种方法均可以将局部放电信号较好的从窄带干扰中提取出来，而且对其发生时间的检测非常精准;但变步长自适应滤波方法具有更快的收敛速度，跟踪能力和稳定性都得到提升。

4 实测局部放电信号滤波处理

为进一步验证该方法的有效性，在实验室条件下，采集了基于Rogowski线圈传感器的电力电缆针刺绝缘缺陷模型的局部放电信号，系统的采样频率为10 MHz，该算例取其中的4 000个采样数据，见图7。

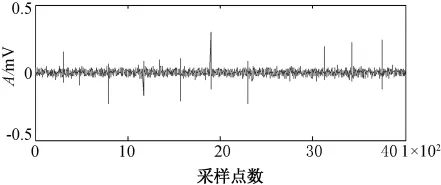
图7 真实局部放电信号

由于实验室条件下，噪声干扰相对较小，为了适应现场环境下的噪声情况，在采集到的真实信号的基础上又叠加了窄带周期性干扰，见图8。图9为最后的去噪结果，从结果可以清晰地看出局放信号在波形快速收敛后较完整的提取出来。

图8 叠加窄带干扰的真实局放信号

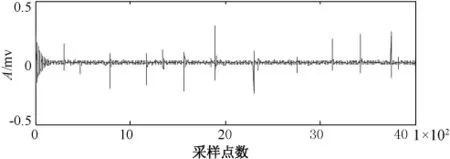
图9 真实局放信号的处理结果

5 结论

针对局部放电的窄带周期干扰抑制的问题，采用了基于EMD和变步长自适应滤波器相结合的方法，依据EMD的自适应分解性能，回避了小波分解过程中小波基函数选取的困难;并且，采用变步长自适应滤波方法，解决了由于定步长所带来的收敛速度和稳定性矛盾的问题。通过仿真及实际信号的处理表明，该方法对局部放电窄带周期干扰的抑制作用，因而有良好的应用潜力和实用价值。

［1］ 邱昌荣，王乃庆.电工设备局部放电及其测试技术［M］.北京:机械工业出版社，1994.

［2］ 陈群，贺健伟，陈灵根，等.基于LS-SVM高精度抑制局部放电信号窄带干扰的研究［J］.电力系统保护与控制，2009，37 (22):22-27.

［3］ 黄成军，郁惟镛.基于小波分解的自适应滤波算法在抑制局部放电窄带周期干扰中的应用［J］.中国电机工程学报，2003，23 (1)，107-111.

［4］ 钱勇，黄成军，戚伟.基于经验模态分解的自适应滤波算法在局部放电窄带周期干扰抑制中的应用［J］.继电器，2006，34 (22):27-31.

［5］ 沈宏，张蒲，徐其惠，等.基于经验模态分解和自适应噪声对消算法的窄带干扰抑制［J］.高压电器.2009，45(1):08-11.

［6］ Huang N E，Wu M C，Long S R，et al.A confidence limit for the empirical mode decomposition and Hilbert spectral analysis［J］. Proceedings of the Royal Society of London.2003(459):2317 -2345.

［7］ Flandrin P，Rilling G，Goncalves P.Empirical mode decomposition as a filter bank［J］.IEEE Signal Processing Letters.2004，11(2): 112-114.

［8］ 贾嵘，徐其惠，田录林，等.基于经验模态分解和固有模态函数重构的局部放电去噪方法［J］.电工技术学报，2008，23(1):13-18.

［9］ 束洪春.电力工程信号处理应用［M］.北京:科学出版社，2009.

［10］ 高鹰，谢胜利.一种变步长LMS自适应滤波算法及分析［J］.电子学报，2001，29(8):1094-1097.