伴随方法在亚轨道飞行器预测制导中的应用

马广富，佘智勇

(哈尔滨工业大学航天学院，150001哈尔滨，magf@hit.edu.cn)

亚轨道飞行器具有较高的飞行速度和高度，但不具备轨道运行的速度和高度.相对入轨飞行器而言，亚轨道飞行器飞行具有高度低，任务目标多样化等特点，因此成为近年来工程技术人员广泛关注的问题，现有文献多为亚轨道飞行器再入及上升轨迹优化及制导，但多数为采用间接参数优化方法求解最优制导轨迹.本文重点研究以固体火箭发动机为动力系统的亚轨道飞行器轨迹优化与制导指令的实现问题，首先基于最优控制理论，利用改进的伴随方法，间接解析的在线生成最优制导指令，其次利用滚动时域控制理论，快速实现对最优指令的跟踪.

1 改进型伴随方法

1.1 轨迹优化方法回顾

直接离线方法［1］是近年来飞行器轨迹优化方法的主流，此方法将控制变量进行离散化，同时按照优化准则，直接调整控制变量的值，直至获得满足性能指标要求的最优解，但求解过程需要的先验知识多，计算量大，计算耗时，并且容易陷入局部极小值而使优化失败.间接法利用最优理论求解问题［2］，间接求解控制变量，可以避免局部极小值的产生，但传统方法收敛速度难以保证，且对协态变量初始值比较敏感［3］.与传统的利用伴随方法求解最优控制灵敏度问题［4］不同，增强型伴随方法对前述2种方法进行了有机的结合，对于具有一定先验知识的初始解，按照间接法逐次迭代，具有收敛精度高，收敛速度快，控制变量平滑等特点.滚动时域控制技术［5］是近年来兴起的一种基于非线性模型的时变跟踪控制方法，具有一定的预测与校正能力，能够保证全局的收敛性与稳定性，对于制导指令的实现具有其他控制方法无法比拟的优势.

1.2 改进型伴随方法

对于具有以下形式的多输入多输出系统:

其中，Z∈Rn×1，F∈Rn×1，对于某一近似满足初始边界与终端边界的轨迹，按照某种指标进行逐次的迭代，直至寻得最优轨迹为止.

设Zk(t)，k≥0为前次迭代轨迹，那么，如果第(k+1)次迭代所产生的Zk+1(t)与Zk(t)满足如下关系:

其中I∈Rn×n为单位阵，β∈Rn×n，0＜‖β‖≤1，将两次迭代的误差表示成变分δZk=Zk+1－Zk，那么在Zk对F(Zk+1)做一阶泰勒展开，即

其中∂F/∂ZT为雅克比矩阵.可以构造辅助方程=－(∂F/∂ZT)Tη，其中η∈Rn×1，那么

由辅助微分方程，利用已知的η(tf)，将其从tf到t0进行反向积分，可求取辅助变量的变化历程，那么可以求得原方程状态的变分初始值为δZ(t0)，并以此为初始值积分，如下所示:

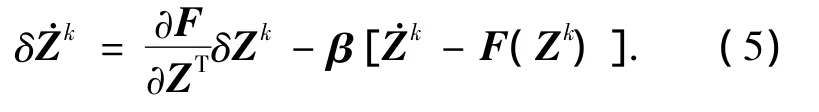
则由已知的当前状态可以求取更为满足约束的优化轨迹状态为

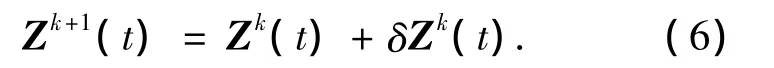
反复进行该过程，可以得到任意精度的最优轨迹.

1.3 改进型伴随方法的收敛性

由于存在关系式(2)，那么下式则必然满足:

2 数学模型

2.1 飞行器动力学模型

采用非线性刚体无因次动力学模型以便于进行数值计算［2］，即

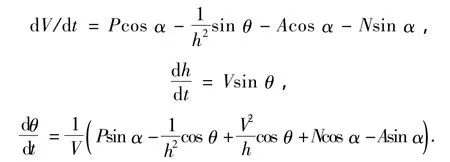
其中:V为速度;h为高度;θ为弹道倾角;α为攻角;P为单位重量的推力;N、A分别为单位重量的法向与轴向气动力.高度用R0无因次化，R0= 6 378 137 m;速度用无因次化，其中g0= 9.806 65 m/s2;时间用无因次化;重力加速度g=.

2.2 边界条件与性能指标

初始边界为

终端边界为

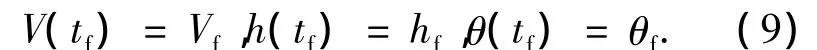
选择BTT转弯方式，不产生相对于风的侧滑角，只对攻角幅值以及变化率进行限制，为

以飞行时间最小(即燃料最省)作为最优性能指标

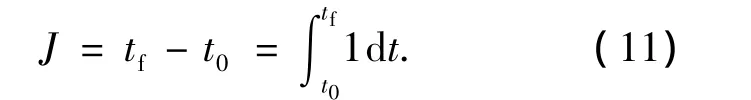
2.3 最优控制问题

以攻角作为最优控制量，求取其随时间的变化历程，在式(8)～(10)的约束条件下，最小化性能指标式(11)，这是典型的两点边值问题，可以利用改进的伴随方法来求解.

2.4 哈密顿函数及协状态

其中

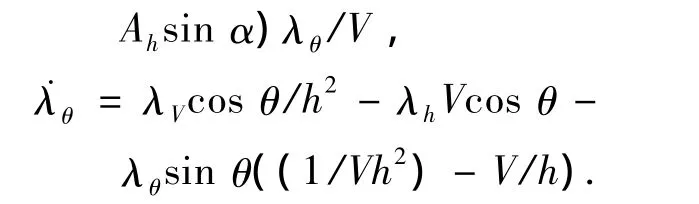
为协态变量方程.

2.5 考虑约束哈密顿函数及协状态

不失一般性，令

为约束方程，且令S=［S1S2］T，

则利用最优控制理论，可以得到哈密顿函数为

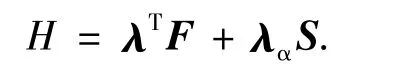
式中λ为协状态向量，满足

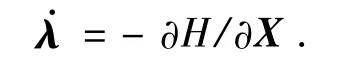
且λα为约束拉格朗日乘子

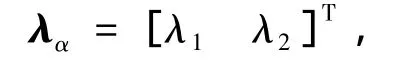
并且满足

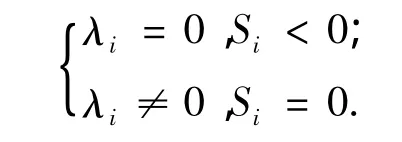
其中∀i=1，2.

注1:对于满足约束的情况，λα被屏蔽;对于在约束边界的轨迹，λα被激活，同时最优控制量由约束方程S获得，λα满足驻点最优控制条件.

3 滚动时域控制

滚动时域控制(Receding horizon control)［6－7］是基于在线计算，不断地根据当前测得的系统状态求解系统的最优控制问题的一种控制技术.设当前时刻为t，状态x，在时域［t，t+T］内，关于系统的最优控制问题为

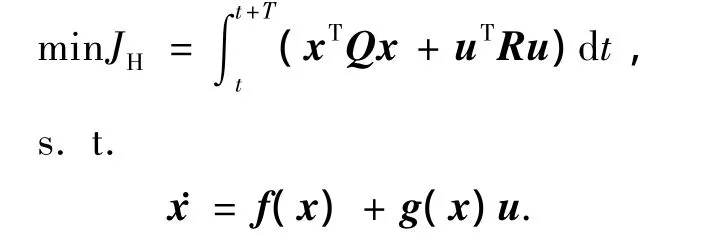
其中T为有限时域.将当前状态测量值作为初始条件，并视为拉格朗日型轨迹优化问题进行求解，在线计算出最优控制解，在时域T内执行控制，直到系统获得新的状态测量值，并将其作为新的初始条件.以相同的方法计算出下一有限时域的最优控制解，该过程不断反复进行直到满足要求，便得到一组状态反馈控制律.显然，该控制方案最重要的是使性能指标不断减少.滚动时域控制只要求对系统当前轨迹中的状态求解最优控制，避免了哈密顿雅可比方法的全局性和难于计算等问题.滚动时域控制的系统渐进稳定性可以参考文献［6－7］.滚动时域控制实现的一般过程如下:

1)在［t，t+T］时间段，按二次型性能指标求取控制u=［utut+T/N… ut+T］;

2)只取ut作为当前时刻的系统输入，驱动系统沿时间轴线前进;

3)在［t+T/N，t+T/N+T］时间段求取控制u=［ut+T/Nut+2T/N… ut+T/N+T］，只取ut+T/N作为当前时刻的系统输入，驱动系统沿时间轴线前进;

4)在不断推进的时间窗口中反复应用滚动时域控制技术，直至飞行任务结束.

3.1 RHC在线求解流程［8］

取权矩阵为

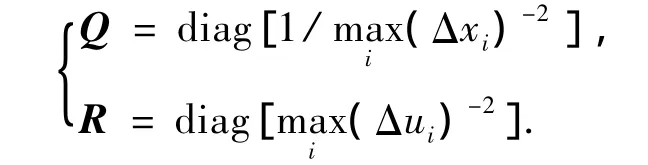
式中Q取为最大状态误差平方的倒数，R取为最大控制变量误差平法的倒数.

将时间域T做N等分，即h=T/N.将状态变量在每个时间步长上做一阶泰勒展开，即

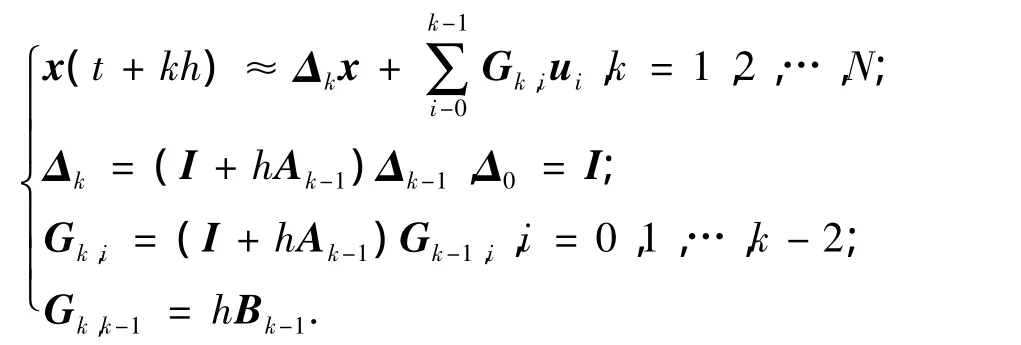
式中:

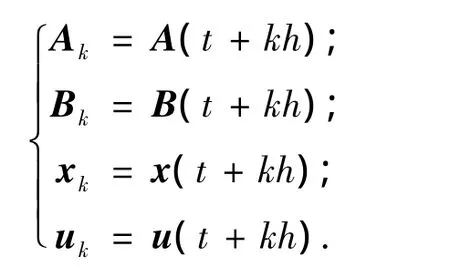
如果令

那么性能指标可以写为

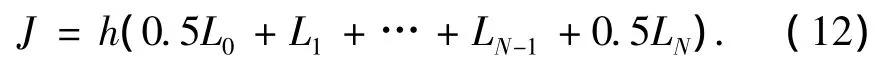
如果将控制序列写为

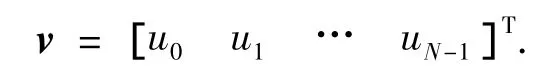
那么，性能指标可以整理为

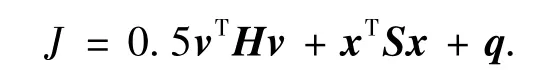
相应各变量均为向量，且易于从式(12)得到.如果有下式成立

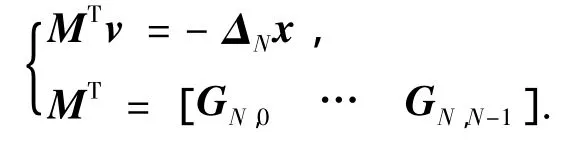
那么可以参考文献［10］，控制变量具有如下式所示的解形式.

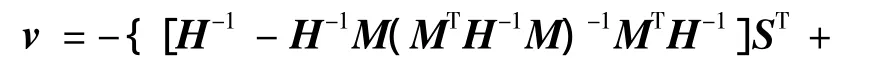
那么，取v的第1个信号为当前控制，同时在下1个仿真周期，继续上述过程.

由求解流程可以看到，RHC控制将微分方程求解转化为代数方程，且是确定代数方程，不存在解方程问题，这大大加快了计算效率，因此可以作为在线求解的有效方式.

4 最优制导指令的生成及实现

将攻角α作为最优制导指令，对飞行器做在线的轨迹优化及跟踪，利用一阶泰勒展开［9－10］，将系统分解为前馈标称输入与反馈控制输入2部分，其系统框图如下.

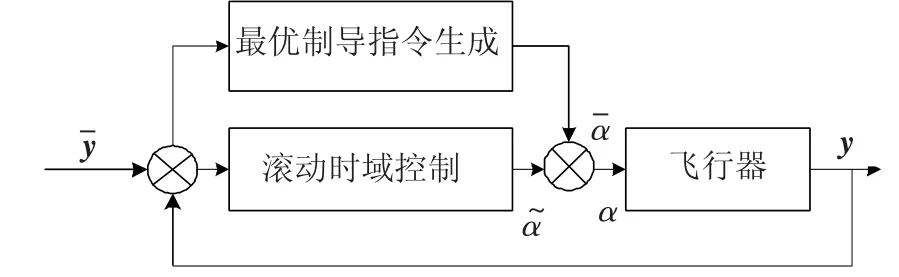
图1 制导系统框图

4.1 最优制导指令的生成

将原系统状态进行增广，与协状态组成新的状态量为

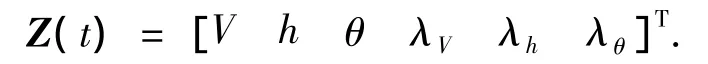
做增广方程

对其实施改进的伴随方法，得到系统前馈标称输入.

取ηV(tf)=［1 0 0 0 0 0］T，那么

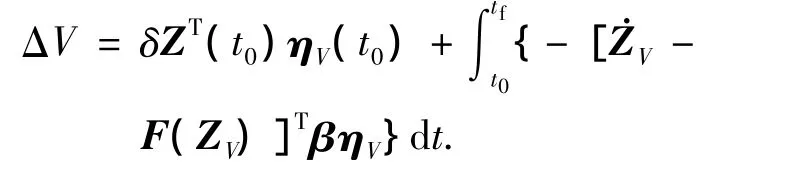
同理Δh，Δθ可得，那么由关系式(4)～(6)可以得到最优系统轨线.同时由最优控制驻点条件∂H/∂α=0及上述状态变量，可以求得最优攻角指令.

4.2 最优制导流程

最优制导流程如下所示:

1)选取初值Z0(t);

2)积分方程˙Z=F(Z，t);

3)求取雅克比矩阵，构造辅助伴随方程;

4)取ηV(tf)=［1 0 0 0 0 0］T，对辅助伴随方程进行反向积分可得到ηV(t);

5)ηh(tf)=［0 1 0 0 0 0］T及ηθ(tf)=［0 01 0 00］T可以确定另外2组条件;

6)为计算考虑，为终端误差增加调整因子，求解方程组为

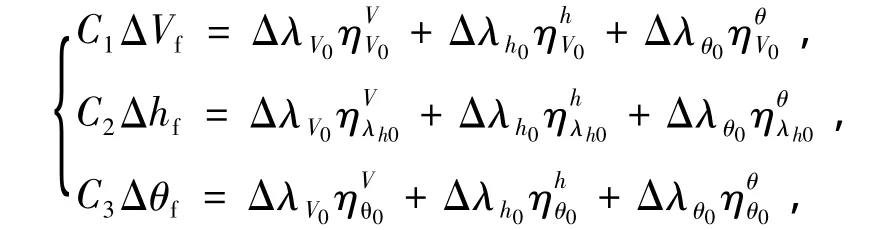
其中0＜Ci≤1，i=1，2，3;

8)重新积分增广状态方程，如满足精度要求则结束，否则返回2).

4.3 最优制导指令的实现

在干扰存在条件下，将系统进行如下建模

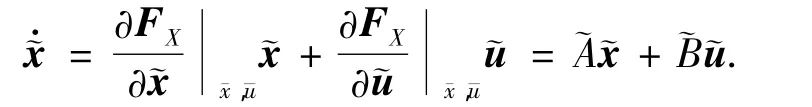
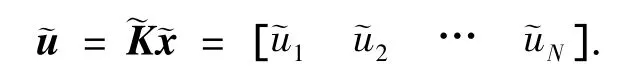
5 算例

5.1 真空环境优化仿真设置

为验证改进型伴随方法的快速有效性，忽略飞行器所受的气动力，以前苏联RD-214火箭发动机为动力模型，研究亚轨道飞行器上升段的轨迹优化问题.各仿真参数设置见表1.

表1 真空环境仿真参数

表1中，状态量的初始与终端边界，协态变量的初始值和初始预估时间用于改进型伴随方法对飞行器轨迹进行优化，时变系统状态矩阵和控制输入矩阵的扰动为验证滚动时域控制的控制效果.

5.2 真空环境优化仿真结果

利用伴随方法的轨迹优化迭代误差分布见表2，其迭代收敛过程如图2～4所示，表中No.为迭代次数，Ve为终端速度误差，He为终端高度误差，Se为终端倾角误差，T为终端时间.由表2可见，经过有限的6次迭代，系统轨线最终收敛到最优轨线，在微型计算机上进行运算，周期不超过1 s，具有完全在线优化的潜力.

表2 迭代误差及飞行时间

图2～4可见整个轨迹的收敛趋势，在不是十分理想的初始估计前提下，改进型伴随方法达到了令人满意的收敛效果，同时具有自动寻找最优工作时间的能力.并且与直接优化方法相比，其控制过程更平滑，且不会陷入局部极小值，这对于制导控制系统实现对制导指令的跟踪具有极大的优势.

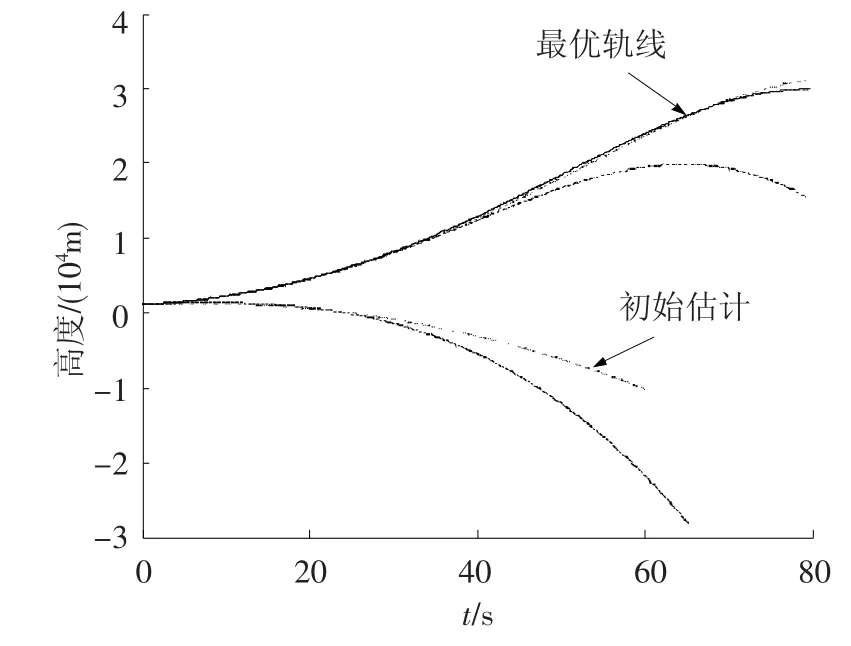
图2 高度收敛过程

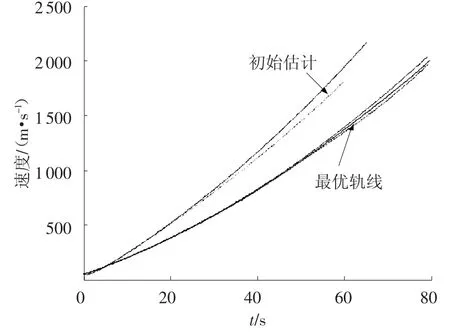
图3 速度收敛过程

5.3 大气层内仿真结果

各空气动力表达式如下:

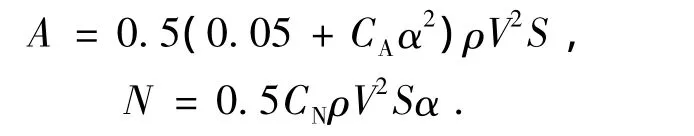
式中:ρ=ρ0e－QhHN为大气密度;CN为法向力系数; CA为由攻角引起的轴向力系数.各参数值如表3所示.

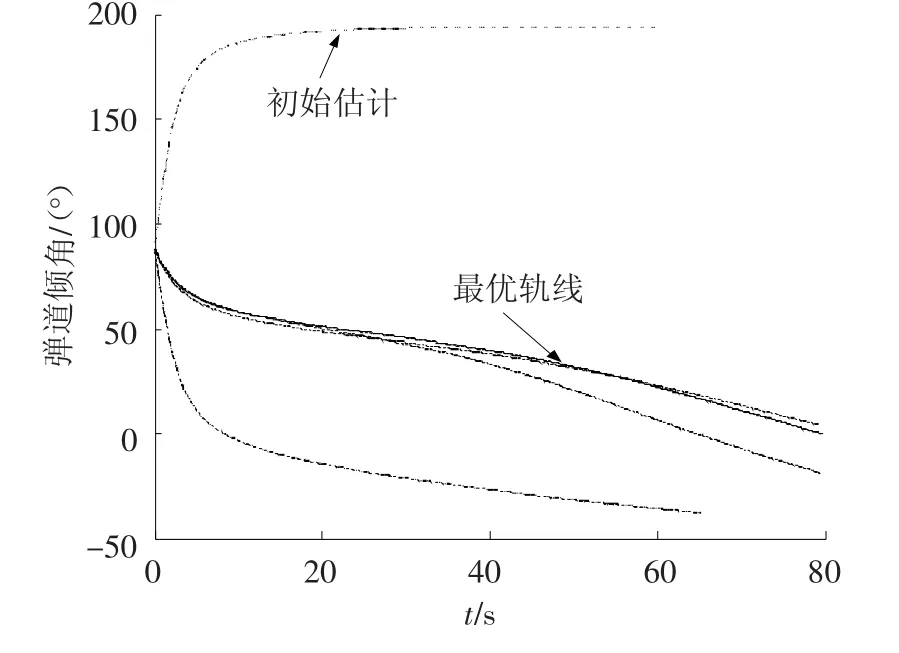
图4 弹道倾角收敛过程

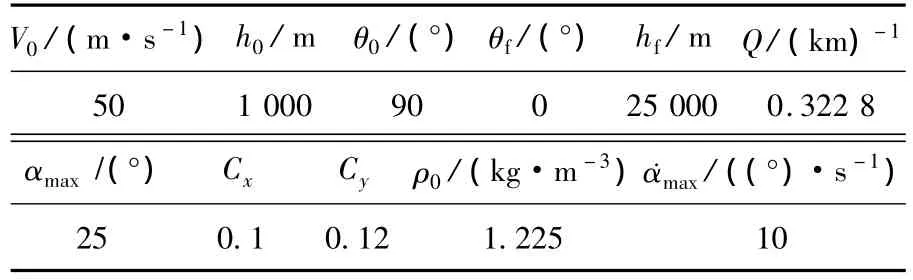
表3 大气层内仿真参数

由图5～6可见，伴随方法能够在有空气存在情况下得到收敛的上升段最优轨迹.

图5 大气内带有控制约束的俯仰角收敛过程

图6 大气内带有控制约束的高度收敛过程

5.4 滚动时域控制仿真结果

在有干扰及不确定的情况下，对优化轨线进行实时跟踪，扰动参数 ‖Δ~A‖、‖Δ~B‖、ΔCx、 ΔCy、ΔP的值分别为5%、5%、10%、10%、5%.

分别对小扰动状态方程的系统矩阵和输入矩阵、阻力系数、升力系数和推力进行扰动，分别利用PID算法和RHC算法对最优轨线进行跟踪，结果见图7.

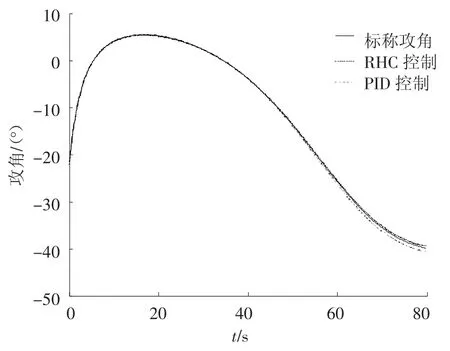
图7 滚动时域控制结果

标称攻角曲线利用改进型伴随方法获取，实际攻角曲线为利用滚动时域控制技术和PID控制所得到的校正控制.仿真结果表明，在存在系统状态矩阵不确定和控制输入扰动的情况下，利用滚动时域控制技术，可以实现对标称最优轨线的在线跟踪与预测校正.并且控制增益比传统PID控制要小.

6 结论

本文提出了一种改进型的伴随方法，基于该方法，对亚轨道飞行器进行了高精度、快速轨迹优化.与间接参数化方法相比，改进型的伴随方法具有收敛精度高、收敛速度快、控制变量平滑等特点，能够避免局部极小值的产生.与传统伴随方法相比，减小了对协态变量初始值的依赖，增大了协态变量的收敛域，具有直接快速在线优化飞行器运动轨迹，实现闭环制导的潜力.对于利用改进型伴随方法得到的制导指令，利用滚动时域控制技术，在外界干扰存在情况下，实现最优轨线的高精度在线跟踪与预测校正.仿真实验表明基于改进的伴随方法的滚动时域控制技术有效、可靠，对外界干扰具有一定的鲁棒性.

［1］丁洪波.亚轨道飞行器上升段轨迹优化与快速重规划［J］.宇航学报，2009，30(3):877－883.

［2］BURROWS R R.Variational problems and their solution by the adjoint method［R］.Huntsville，Ala:Technical Memorandum，1966，NASA-TM-X-53459.

［3］赵吉松，谷良贤，潘雷.月球最优软着陆两点边值问题的数值解法［J］.中国空间技术，2009，29(4): 21－27.

［4］SILLY-CARETTE J，LAUTRU D，GATI A，et al.Optimization of the homogenization of tissues using the adjoint method and the FDTD［C］//2008 IEEE MTT-S International on Microwave Symposium Digest.Atlanta，GA:［s.n.］，2008:1361－1364.

［5］罗德林.基于滚动时域控制的寻的末制导律研究［J］.南京航空航天大学学报，2005，37(1):52－56.

［6］KATSARGYRI G E，KOLMANOVSKY I，MICHELINI J，et al.Path dependent receding horizon control policies for Hybrid Electric Vehicles［C］//2009 IEEE conference on Control Applications＆Intelligent Control.St.Petersburg，:［s.n.］，2009:607－612.

［7］MAYNE D Q，MICHALSKA H.Receding horizon control of nonlinear systems［J］.IEEE transaction on automatic control，1990，35(7):814－824.

［8］LU P.Closed-form control laws for linear time-varying systems［J］.IEEE Transactions on Automatic Control，2000，45(3):537－542.

［9］WU F，PACKARD A，BALAS G.LPV control design for pitch-axis missile autopilots［C］//Proceedings of the 34th IEEE Conference on Decision and Control.New Orleans，LA:［s.n.］，1995:188－193.

［10］ZHU J J，BANKER B D.X-33 ascent flight control design by trajectory linearization-a singular perturbation approach［R］.Denver，CO:AIAA，2000:1－19.