实时递推的最小二乘预测跟踪算法

周姗姗，柴金广，李丹

（中国科学院上海技术物理研究所，上海200083）

对于一个探测系统来说，从传感器采集图像，到系统处理数据、识别目标、伺服控制、跟踪目标的过程中，由于系统延时，会导致跟踪数据的延迟，造成跟踪误差。此外，目标发生机动时，由于运动的速度和方向发生改变，也会造成实时跟踪的困难。为了补偿跟踪误差，达到实时、稳定跟踪目标的目的，本文提出了一种实时递推的最小二乘预测跟踪算法。

最小二乘法最早是由Gauss为进行行星轨道预测的研究而提出的[1]，现在最小二乘法已成为用于目标跟踪的常用方法之一。与其他方法（如：α-β-γ滤波、卡尔曼滤波）相比，最小二乘原理简单，易于理解和掌握，且在一定条件下具有良好的统计性，因而更具有工程实现的意义。本文基于最小二乘法的原理，结合平方预测器的估算方式，采用递推参数计算来实现目标的位置预测，解决由于系统误差、目标机动等因素造成的跟踪延迟、目标丢失的问题。

1 预测跟踪算法

图1给出了预测跟踪算法的流程图，系统每读入新的一帧图像，替换最旧的一帧历史数据，根据保存的帧目标数据递推计算目标轨迹参数，并由此预测下一帧目标位置。

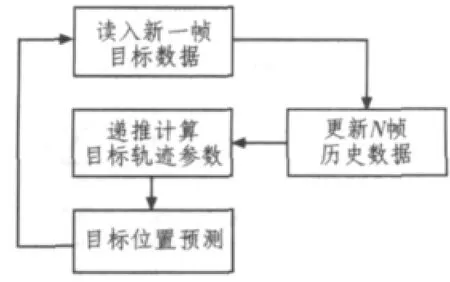
图1 预测跟踪算法流程图Fig.1Flow chart of predicted tracking algorithm

1.1 最小二乘原理

在探测系统跟踪目标的过程中，目标的运动速度及方向会按照一定的运动规律随时间不断变化，为了从观测数据中提出有用信号，首先需要对目标的运动规律做出假设[2]。

通常假设目标函数f（t）在N个顺序时刻的观测值为f（ti）（i=1，2，…，N），最小二乘的基本思想即选择一个多项式p（t）用一种使均方误差（在某种意义下）为极小的方式来逼近f（t）[3-4]。

对于探测系统来说，观测值是离散的数据，可以确定一组a0，a1，…，am（m＜N）系数，使得观测值和逼近值的N点均方误差

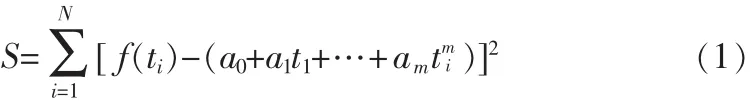
最小。

最小二乘多项式p（t）表示为

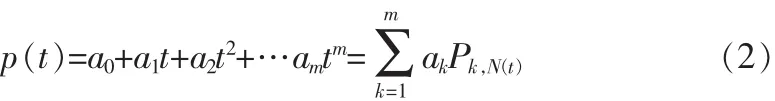
通过S对ak求偏导数，令偏导数为0，可得到多项式的通解：

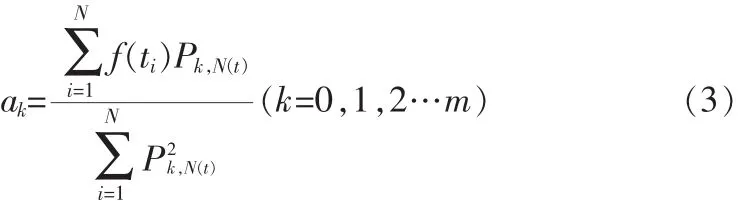
1.2 平方预测器

平方预测器以线性二次曲线作为目标函数f（t）的最佳逼近，即多项式p（t）表示为

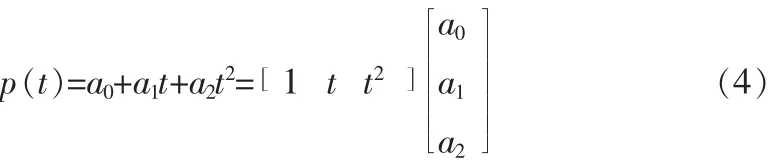
则N点均方误差为

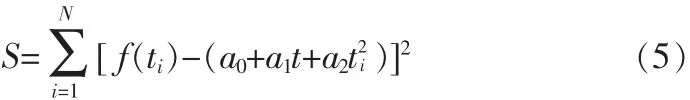
运用最小二乘原理，计算最小均方误差下最佳线性逼近的通解，即多项式系数a0、a1、a2，可以得到[5]：

式中，bmn（m，n=1，2，3）为行列式|M|的余因子，且|M|≠0。

1.3 实时递推计算公式

考虑到实际应用中，在较短时间内，目标的运动或参数变化总可以用二次或低次函数描述[6]，因此运用平方预测器得到的一组参数α，β，γ总可以最佳逼近某一段时间内目标的运动轨迹，但随着时间的增长，目标运动可能发生变化，原来的参数不再满足目标运动的规律。因此，本文对于N点最佳线性逼近，采用实时更新参数的方式，即在每个目标数据采样时刻k+N，利用历史时刻k，k+1，…k+N-1，的N个点的测量值重新计算二次曲线的参数α，β，γ，以确保预测轨迹与真实目标轨迹的最佳逼近。因此，将上节公式（6）改进后可以得到实时递推的参数计算公式：

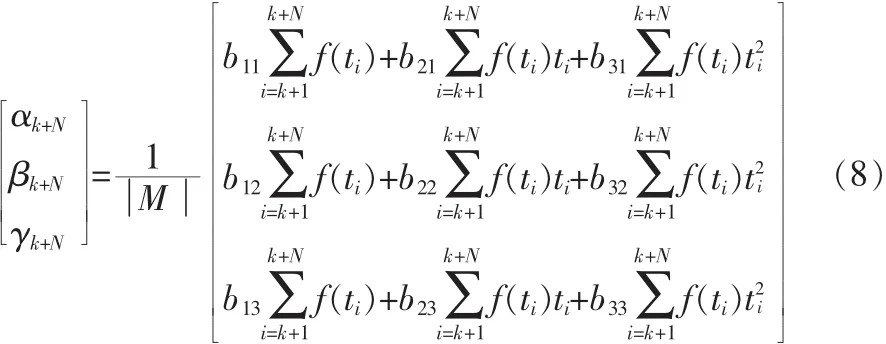
式中，k=0，1，2，…。

2 仿真实验

为验证算法在工程应用上的可行性，本文基于Matlab软件针对系统延迟、目标机动这两种情况进行了模拟仿真，本次实验选取N=5。

图2给出了真实轨迹在没有发生系统延迟情况下的目标预测跟踪轨迹与真实轨迹的比较结果。可以看到目标在某一段时间内发生机动改变了轨迹方向，给定的目标轨迹采样周期为T=0.005 s。

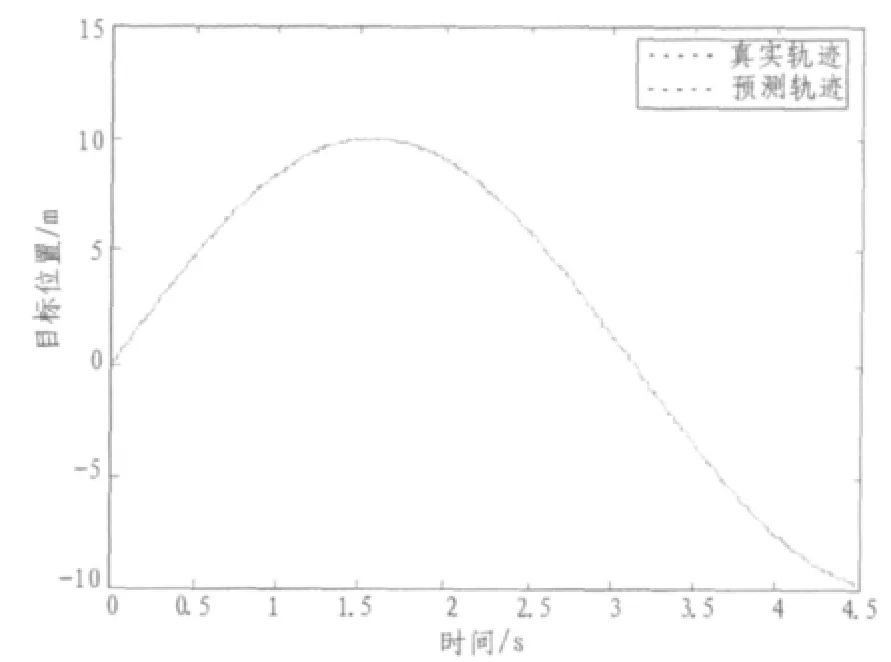
图2 未发生延迟的预测跟踪轨迹与真实轨迹的比较图Fig.2Comparison of predicted tracking and real tracking at system in-time

考虑实际工程应用中的情况，假设系统延迟时间为一个采样周期。图3（a）给出了目标预测跟踪轨迹与真实轨迹的比较结果，图3（b）为图3（a）轨迹初始部分的放大比较图。

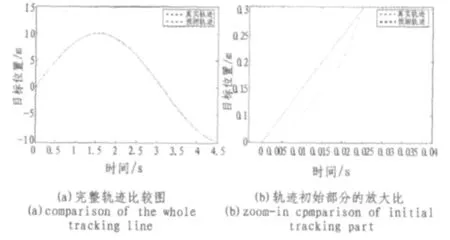
图3 发生延迟的预测跟踪轨迹与真实轨迹的比较图Fig.3Comparison of predicted tracking and real tracking at system delay

如上图可以看到预测跟踪轨迹能够很好地逼近真实轨迹，在发生系统延迟的情况下，从图3（b）可以看到由于采用了5点平方预测，经过初始阶段的5个采样周期后，目标轨迹误差得到补偿，并迅速逼近真实轨迹，此外，从图3（a）中可以看出，当目标机动时，轨迹方向发生明显改变，预测跟踪轨迹仍旧能很好地逼近真实轨迹。

最后给出了预测轨迹与真实轨迹的误差百分比，图4（a）为系统未延迟时的误差百分比，图4（b）为系统延迟时的误差百分比。表1则给出了两种情况下具体的误差百分比比较。

图4 两种情况下的系统误差百分比Fig.4Error percentage of the two cases

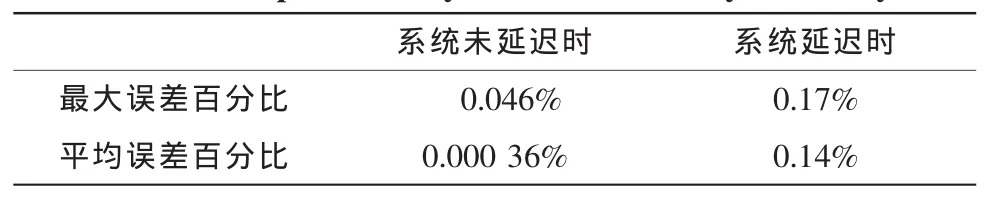
表1 系统未延迟与延迟情况下的误差百分比比较Tab.1 Comparison of system in-time and system delay

如表1所示，虽然在系统延迟的情况下，预测轨迹与真实轨迹的误差百分比较大，但平均误差百分比控制在了0.15%以内，且可以看出预测跟踪轨迹还是很好地逼近真实轨迹，没有出现轨迹偏移发散的情况。

3 结束语

本文提出的实时递推的最小二乘预测跟踪算法，采用平方预测器的二次曲线函数作为目标轨迹的最佳逼近，经过最小二乘估算得到的多项式通解，具有运算简便、易于实现的特点。结合工程实际情况，改进后的算法通过仿真实验验证，跟踪效果理想，具有工程应用的可行性。今后根据不同工程的指标要求，算法还可以在参数细节上进行修改，以达到最佳的预测跟踪效果。

[1]强明辉，张京娥.基于MATLAB的递推最小二乘法辨识与仿真[J].自动化与仪器仪表，2008（6）：4-5，39.QIANG Ming-hui，ZHANG Jing’e.RLS identification and simulation based on Matlab[J].Automation&Instrumentation，2008（6）:4-5，39.

[2]徐瑜，杨绍清，孙牧.最小二乘滤波在目标跟踪中的应用[J].指挥控制与仿真，2007，29（4）：41-42.XU Yu，YANG Shao-qing，SUN Mu.Application of least square filtering for target tracking[J].Command Control&Simulation，2007，29（4）：41-42.

[3]F.施依德.全美经典数值分析[M].2版.罗亮生，包雪松，王国英译.北京：科学出版社，2002.

[4]张起贵，张魁.基于最小二乘直线拟合的小目标检测[J].电子设计工程，2010，18（7）：176-177，180.ZHANG Qi-gui，ZHANG Kui.Based on least-squares linear fiting for small targets detection[J].Electronic Design Engineering，2010，18（7）：176-177，180.

[5]杨耿.运动目标的图像识别与跟踪研究[D].江苏：江苏大学，2005.

[6]秦暄，章毓晋.一种基于曲线拟合预测的红外目标的跟踪算法[J].红外技术，2003，25（4）：23-25，31.QIN Xuan，ZHANG Yu-jin.A tracking method based on curve filtering prediction of IR object[J].Infrared Technology，2003，25（4）:23-25，31.