惯导平台历次测试数据时间序列建模分析
2011-03-14姜泉璐汪立新吴玉彬杨建业吕永佳
姜泉璐,汪立新,吴玉彬,杨建业,吕永佳
(第二炮兵工程学院304教研室,陕西西安710025)
时间序列是随时间变化而又相互关联的数据序列,通常把按时间顺序排列的观测数据序列称为一个时间序列。由文献[2]可知,时间是影响惯导平台稳定性的主要因素,随着时间的推移部分惯导平台参数的稳定性会发生比较明显的变化。因此研究惯导平台参数的时间特性是非常必要的。惯导平台的测试虽然是以一定的时间顺序来进行的,但受到测试时机的限制并非等时间间隔的。
惯导平台具有稳定期指标,但实际很难保证在每个稳定期内都对惯导平台进行测试,得到的数据都比较零乱。直接对这些数据进行研究,很难找到描述惯导平台测试数据的规律。同时由于测试次数较少,也更增加了描述其时间特性的难度。样条函数插值[1]不仅能克服以往插值方式局部特性较差,在端点附近精度较差的不足,而且稳定性好,并能保持较高的精度,比较适合在惯导平台测试数据时间序列中应用。本文将采用样条函数插值法来构建惯导平台测试数据需时间序列,为建模分析提供基础。
1 问题描述
惯导平台的测试是根据不同需要来进行的,测试的时间间隔不固定。在这种情况下,要通过一次插值来产生惯导平台误差系数的时间序列,其误差必然很大且插值点很不均匀。从文献[3]可以看出,惯导平台误差系数的正态性并不是很好,带有很大的随机性。为此,提出了二次修正插值法,通过两次使用样条函数插值法来构造惯导平台测试数据的时间序列。第一次插值完成后,对插值结果进行修正,在此基础上再进行第二次插值,从而获得所需的惯导平台测试数据的时间序列,为其时间序列建模分析创造条件。
2 平稳时间序列线性模型
平稳时间序列...,Z-2,Z-1,Z0,Z1,Z2,...,一般EZt=μ≠0,为方便起见,令Wt=Zt-μ,显然EWt=0。于是得到序列
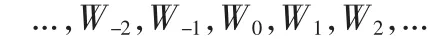
容易验证它仍然是平稳时间序列。均值为零具有有理谱密度的平稳时间序列可表示为下面三种形式的一种。
1)自回归模型任何一个时刻t上的数值Wt可表示为过去p个时刻上数值Wt-1,Wt-2,...,Wt-p的线性组合加上t时刻的白噪声,即可表示为:

其中常数p为模型的阶数。自回归模型简记为AR(p)。
2)滑动平均模型Wt可表示成白噪声{at}在t和t以前q+1个时刻上数值at,at-1,at-2,...,at-q的加权和,即可表示为:
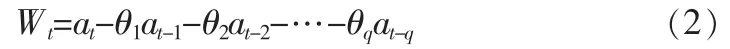
其中常数q为模型的阶数。滑动平均模型简记为MA(q)。
3)自回归滑动平均模型自回归滑动平均模型可表示为:

p,q为模型的阶数,自回归滑动平均模型简记为ARMA(p,q)。
3 时间序列的平稳性检验
平稳性检验[4-6]主要用来检验所构建的时间序列是否具有不随时间推移而变化的统计特性。平稳性检验的方法有参数检验法和非参数检验法。前者在检验中需要知道子样参数的抽样分布,而且计算起来相当麻烦,故通常采用后者。非参数检验法是在未知子样参数抽样分布情况下的检验方法。在实际工作中最常用的是逆序检验法,其基本原理是:若数据y1,y2,…,yn平稳,则分段子序列的均值与方差应无显著差异。
将{yt∶1≤t≤n}按长度M分成K个等长度的子序列(余数可不用),记为n/M。

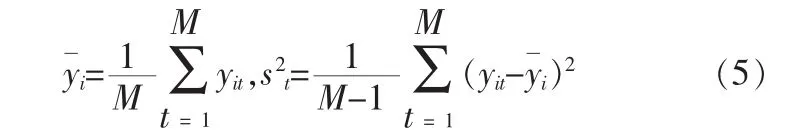
其中k,M的选取依数据长度n而定。定义

文献[1]表明:若{yi∶1≤i≤n}具有平稳性,则当M足够大独立同分布的,且有
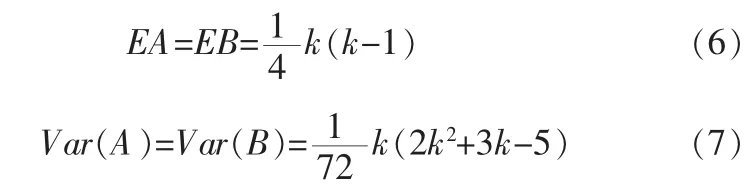
统计量
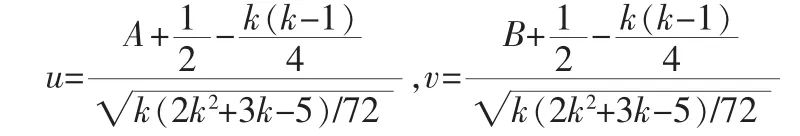
均近似服从N(0,1)分布。
由此得到{yt∶1≤t≤n}平稳检验的步骤如下:
1)均值平稳性检验的步骤[7]①将{yt∶1≤t≤n}分成k段,每段n/k个数据,并相应计算各段均值,得到均值序列{∶1≤i≤k};②计算A及u;③由给定置信水平,查标准正态分布得Za/2;④若|u|<Za/2,则以置信度1-a认为该残差数据序列具有平稳性,否则认为是不平稳的。
2)方差平稳性检验的步骤步骤同1的均值性平稳检验步骤,只是{yt∶1≤t≤n}分段后计算每段的方差,得到方差序列{∶1≤i≤k},在计算B及v,并进行检验。
4 二次修正插值法
4.1 第一次修正插值[8-9]
针对惯导平台标定结果具有稳定期这一要求,以其稳定期为时间单位,采用三次样条函数插值法,对惯导平台历次标定结果进行第一次插值,以历次标定结果作为插值的基本点,对于稳定期内有多次测试的,取其平均值作为基本点。然后,以稳定期为单位选择插值点进行插值。这种方法比较符合惯导平台测试数据变化的特点,对插值点的准确性进行检验的方法是以基本点为依据,以稳定期内的指标为标准,对插值点进行检验和修正,最终获得一个以稳定期为基本时间单位的时间序列。称此时间序列为基本时间序列。
4.2 第二次修正插值
第二次插值的目的是为了扩大样本容量,解决小样本建模的问题。通过第一次样条函数插值之后,获得了惯导平台历次测试数据的一个基本时间序列,其样本容量相对较小。按照目前惯导平台的实际情况,所获得时间序列的容量一般很小,要用一个很小容量的样本进行建模,无法得到一个准确、完整的模型,也无法准确预测惯导平台误差系数的变化趋势。为此,文提出了第二次修正插值,即在第一次插值所得的时间序列的基础上进行再插值,用于扩大样本容量。插值的原理依然是三次样条函数插值法。第二次插值时以第一次插值所得时间序列的元素作为基本点,在相邻的两个基本点之间进行等点数插值,插值点的个数可根据建模所需样本容量来选取,一般要使第二次插值所得的时间序列的样本容量大于50。插值结果将用第一次修正插值的方法进行检验和修正,以保证任意相邻的两个基本点之间的插值结果满足稳定期稳定性要求。
5 应用举例
现以某惯性平台的误差数D1为例来构建惯性平台测试数据的时间序列,该惯导平台3年共测试14次,其中第一年3次,第二年6次,第三年2次,第四年3次,由历次测试数据构成的序列称为原始时间序列,如表1所示。在4年的时间内,共得到11个基本点。
在基本点的基础上用三次样条函数法进行第一次插值,插值结果如表2所示。共得到3个插值点,这3个点与基本点一共14个点,就构成了某惯性平台¥误差系数的基本时间序列。

表1 原始时间序列Tab.1Original time series

表2 基本时间序列Tab.2Basal time series
在基本时间序列的基础上用同样的方法进行第二次插值,在每相邻的两个基本点之间插入3插值点,得到一个样本容量为53的二次插值时间序列。基本点、插值点对应的曲线图如图1所示。
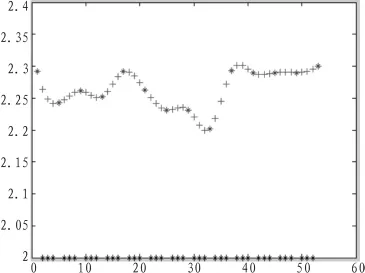
图1 插值前后比较示意图Fig.1Interpolation before-and-after schemes
图1为插值前后比较示意图,“*”为基本点,“+”为插值结果。横轴上的“*”为绘图辅助点,没有任何意义。
预测结果与实际结果比较图如图2所示。预测结果与测试的变化趋势很接近。将测试结果和预测结果按时间顺序合并在一起可按其变化趋势来判断误差系数稳定性,能够体现惯导平台性能的变化趋势。

6 结论
提出的二次修正插值法为惯导平台误差系数的时间序列建模提供了一种研究方法和途径,特别是非等时间间隔小样本条件下的建模,具有较好的工程应用价值。利用该方法可以达到两个目的:其一是能科学分析惯导平台的长期稳定性,有效地较少测试次数;其二是和射前标定技术相结合以延长惯导平台的稳定期,并利用一次通电特性提高惯导平台的使用精度。
[1]周刚.平稳性检验方法研究[D].长沙:国防大学,2004.
[2]徐军辉.捷联惯性测量数据分析方法研究[D].西安:第二炮兵工程学院,2003.
[3]肖正林,徐军辉,钱培贤.惯性组合误差射前标定方法研究[J].弹箭与制导学报,2004,24(4):362-366.XIAO Zheng-lin,XU Jun-hui,QIAN Pei-xian.Research on the calibration method for IMU errors before launching[J].Journal of Projectiles,Rockets,Missiles and Guidance,2004,24(4):362-366.
[4]秦永元.惯性导航[M].北京:科学出版社,2006.
[5]王振华.惯导平台稳定回路的改进设计研究[D].哈尔滨:哈尔滨工程大学,2004.
[6]王海淼,万彦辉,孟卫锋.无模型自适应控制策略在惯性平台调平系统上的应用[J].战术导弹控制技术,2006,52(1):86-103.WANG Hai-miao,WAN Yan-hui,MANG Wei-feng.Application of model-free self-adaptive control tactics to the leveling system of platform inertial navigation system[J].Control Technology of Tactical Missile,2006,52(1):86-103.
[7]李清梅.石英挠性加速度计温度误差建模与补偿技术研究[D].长沙:国防科学技术大学,2005.
[8]Klawonn F,Kruse R.Constructing a fuzzy controller from data[J].Fuzzy Sets and System,2003,85(2):66-72.
[9]Kinouchi M,Iwatusk N.Application of fuzzy PI control to improve the position accuracy of a rotary-linear motor driven by two dimensions.ultrasonic actuators[J].Microprocessors and Microsystems,2000,24(2):45-50.
