干道信号交叉口群协调控制系统中的影响因素
2011-03-12邵春福
马 楠,邵春福,赵 熠
(1.北京交通大学城市交通复杂系统理论与技术教育部重点实验室,100044北京,manan0613@gmail.com; 2.美国内华达大学里诺分校土木与环境工程学院,89557内华达)
交通干道是城市内部交通的动脉,它承担了城市交通网络中大部分交通负荷.因此,保证干道交通流的畅通、高效行驶,对提高城市道路网的顺畅、安全运行有着至关重要的意义[1].针对干道协调控制的研究始于上世纪60年代,美国国际商用机器公司(IBM)的工程师Brooks[2]首次提出了两相位的协调控制优化算法.
90年代初,全永燊[3]研究和分析了协调控制的理论与方法.随后,国内学者从多个方面利用不同方面对该领域进行了大量研究.常云涛等[4]将遗传算法引入相位差计算,对干道协调控制方法进行了优化;刘灿齐[5]提出利用基于双层规划的优化模型来计算协调控制系统的绿信比;袁二明等[6]研究了基于混合整数规划的协调控制问题;李振龙等[7]针对“智能体”影响下的交叉口进行了协调控制博弈分析;孙超等[8]则提出了通过模糊控制的算法解决协调控制的问题.在针对不同的优化目标方面,万绪军等[9]以双向车辆延误最小为目标函数,分析了线控系统中相位差优化的问题;刘东等[10]则对近距离交叉口下的协调控制方案进行了分析;此外,卢凯等[11]以干道控制系统的总延误与总停车次数作为优化目标进行了相关问题的研究;马楠等[12]提出了基于双向绿波带宽最大化的干道协调控制优化模型.尽管上述研究成果已从各个角度对干道协调控制的方法进行了较为深入、全面的研究,但在实际应用中,仍然存在2个问题亟待解决:
1)相位相序优化对绿波优化的影响.上述针对协调控制优化的研究大都假设交叉口群的相位相序为已知条件,对系统的协调控制优化只能在给定的相序条件下进行优化,而无法进行相序调整.但事实上,相序优化是绿波优化中极为关键的因素之一,因此在干道协调控制系统优化之前如何计算出最优的相序方案则显得极为重要.
2)交叉间距对绿波优化的影响.目前针对干道交叉口协调控制优化的研究中,大都推测判定在交叉口群中各交叉口间距相等或相近的情况下,系统更加容易获得较大的双向绿波带宽.
针对上述2个问题,本文根据NEMA(National Electrical Manufacturers Association Phase)相位优化理论[13],在交叉口数目为2~10时9种不同条件下,针对交叉口间距相等或不等的2种情况,随机生成5 000×9×2组仿真场景.随后,利用本文方法对上述仿真场景进行了双向绿波优化.
1 NEMA相位及其对相序优化的影响
NEMA双环相位结构由双环、双段(Stage)共8个相位构成(见图1).任意调整位于同环、同段中2个相位的时长和顺序,不会对交叉口中其他相位的正常运行产生任何不良影响.与传统的“四相位”方案相比,NEMA相位在主路先行的情况下,其潜在相序方案由4种提升至16种,极大提高了相序优化的可操作性.
针对上述相位,假设东西方向的相位Φ2和Φ6为干道协调控制相位,相位Φ6为主要方向相位,那么干道相位相序可分别设置为左转提前(Leading,简称P1)、左转滞后(Lagging,简称P2)和提前—滞后(Lead-Lag)3种情况,其中提前—滞后情况又可分为主向左转提前(Lead-Lag,简称P3)和次向左转提前(Lag-Lead,简称P4)2种,见图2.

图1 双环结构NEMA相位
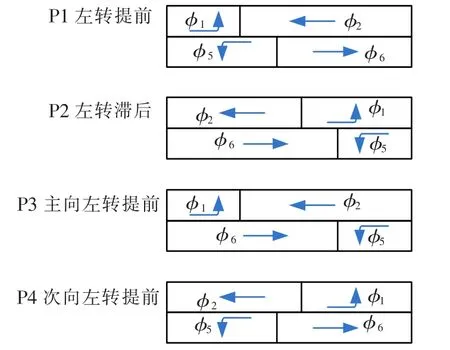
图2 NEMA双环结构中4种相位相序方案
2 基于相位相序调整的绿波带宽优化模型
在Brooks提出针对两相位信号交叉口的绿波带宽优化模型之后,Morgan[14]和Little[15]利用整数规划对仅考虑主路直行相位情况下的绿波优化问题建立了解析模型,确保主路双向同时能够获得相同的绿波带宽.随后,Messer[16]在上述研究基础上,提出了包含左转相位的绿波带宽优化算法.该算法被广泛使用在 PASSER II、MAXBAND等众多带宽优化软件中[17].
本文在Messer的算法基础上,通过迭代历遍的方法,对NEMA相位结构中不同信号相位相序下的最优带宽进行计算,最后得出系统整体最优的绿波带宽.该优化模型可表示为
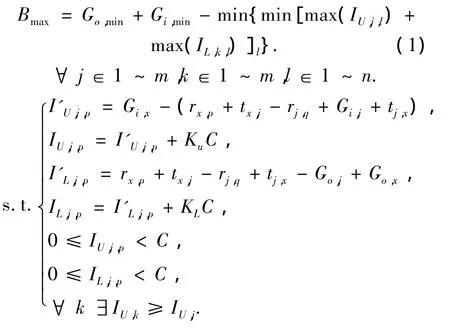
式中:Bmax为系统最优的绿波带宽;Go,jGi,j分别为j交叉口主、次要方向直行的绿灯时长;I'U,j,p,I'L,j,p分别为在p相位条件下,j交叉口绿波带宽的上端、下端损失时间;IU,j,p,IL,j,p分别为调整后的交叉口绿波带宽上端、下端损失时间;tx,j为交叉口x到j的行驶时间;rj,q为j交叉口次要方向绿时长Gi,j相对主要方向绿时长Go,j在相序方案q下的相对相位差;x为主向直行绿信号时长最短的交叉口标号;m为系统中信号交叉口数目;n为相序组合方案,由于每个交叉口相序均有4种情况,故n=m4;KU,KL∈Z为调整系数,确保0≤IU,j,p,IL,j,p< C.
假设由5个交叉口组成的某干道系统的配时方案如表1所示,上述模型针对该系统的具体求解过程如下.
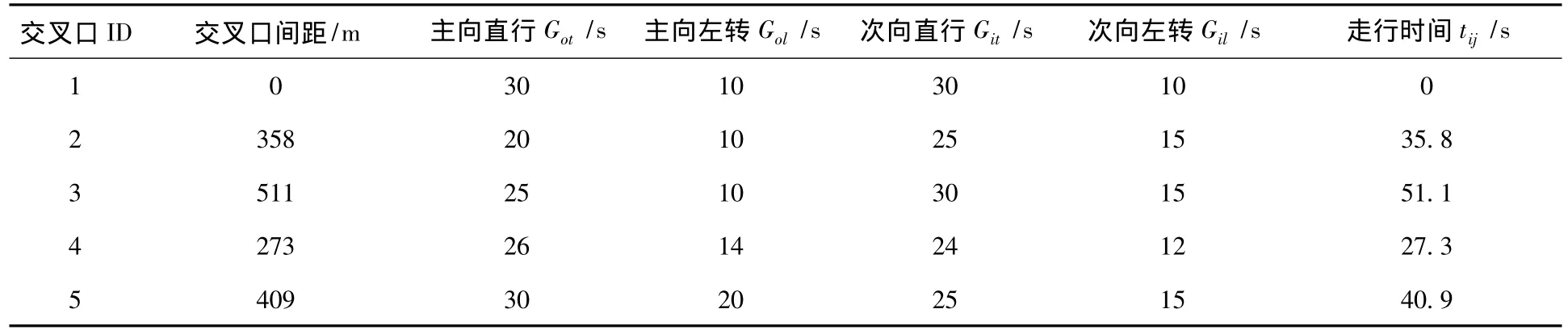
表1 交叉口基本参数
步骤1:找出主向直行绿灯时间最短的交叉口x=2,并重新计算各交叉口至该交叉口的相对走行距离和行驶时间.
步骤2:根据各交叉口相序,计算

步骤3:根据式(1)计算上端、下端损失时间IU,IL,假定本例中5个交叉口的相序分别为P4、P4、P1、P1、P4,计算结果见表2.
步骤4:跟据上端损失时间对上述交叉口进行排序,排序结果见表3.
步骤5:针对该相序条件,建立最小损失时间矩阵,求解该条件下的最小损失时间为7.2 s,如表4所示.针对该方案的双向绿波带宽为Go,min+ Gi,min-Imin=20+24-7.2=36.8 s,基于该优化结果的双向绿波如图3所示.

图3 优化后双向绿波带
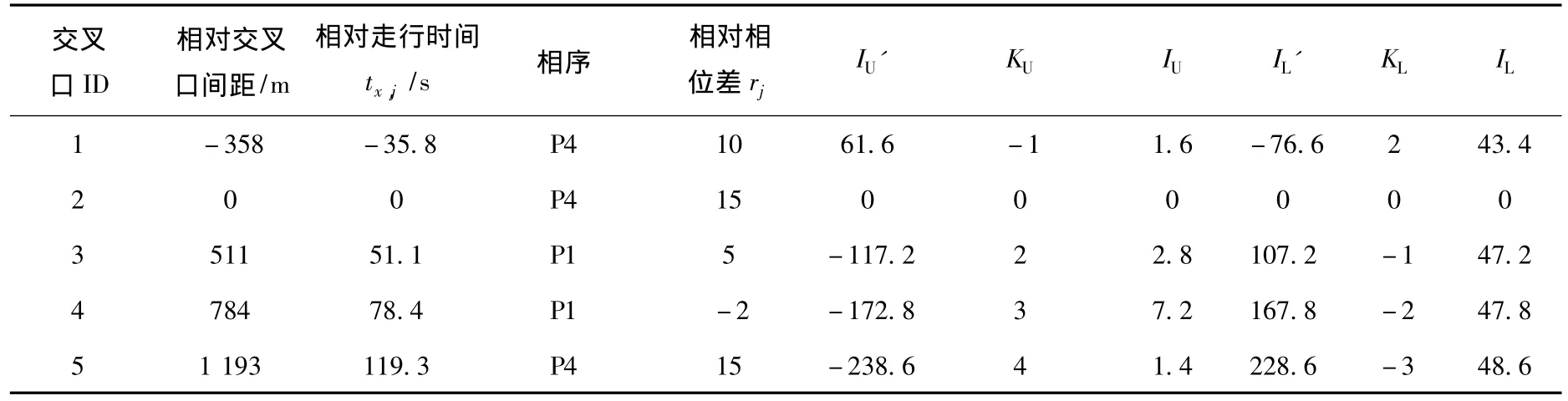
表2 交叉口计算参数
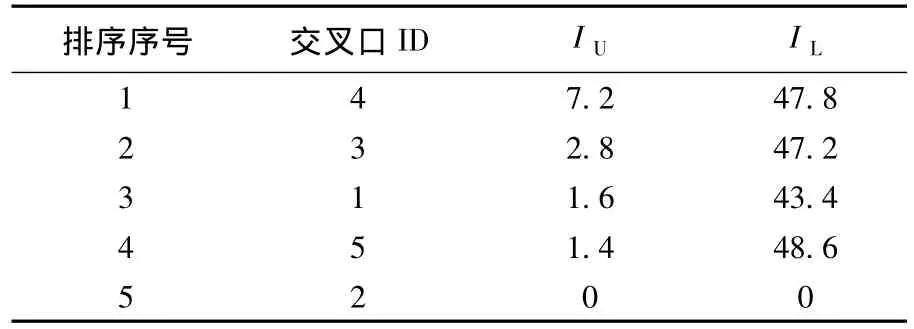
表3 上端损失时间排序
步骤6:历遍交叉口相序组合情况,重复步骤1~5,求得系统最优的最大绿波带宽.本文提到的干道系统,恰好在上述相序条件下能得到最大的双向绿波带宽.
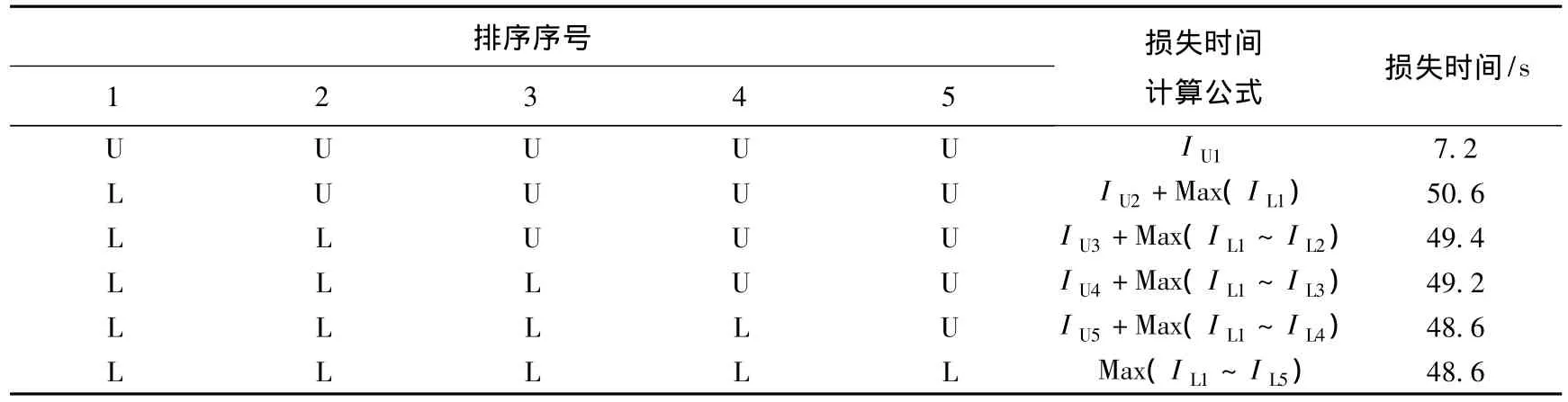
表4 最小损失时间求解矩阵
3 交叉口间距对干道系统协调的影响
根据上述方法,设计了干道协调控制优化的计算机仿真程序.该程序能够在给定范围内(交叉口数目,周期,走行时间等参数),随机生成若干组干道系统,并针对上述随机生成的干道系统得到最大绿波带宽,以及实现该绿波带的信号交叉口相序方案.
针对随机生成的干道系统,有如下假设:1)在交叉口数目为2~10的9种模拟干道系统中,分别针对交叉口间距不等 (Random Distance,RD)和等(Uniform Distance,UD)2种条件各生成5 000组随机场景,即共5 000×9×2=90 000组仿真场景用来进行对比分析;2)随机生成的干道系统中,信号周期范围为30~200 s;3)主路方向绿灯总时长为周期的50%~90%,协调控制相位绿灯时长为主路绿灯总时长的50%~90%,故协调控制相位绿灯时长为周期时长的25%~81%; 4)相邻信号交叉口之间的走行时间范围为60~200 s;5)由于支路信号相位和相序对干道协调控制优化没有影响.因此,在本仿真中没有随机生成支路信号;6)针对某一干道系统,当有若干组相序方案均能得出同样的最大带宽时,本程序将记录所有可能的相序方案.若求解得到的最大绿波带宽等于Go,min时,则认为该系统无绿波优化方案.仿真结果见图4.
图4a)、b)中P1相序在交叉口间距不等和相等2种情况下的使用比例均值分别为21.8%和21.4%;P2相序在上述2种情况下的均值分别为21.9%和21.3%.能够看出这2种相序的使用比例在优化后的干道系统中较为相似.其中,当交叉口间距不等时,P1相序占总数的百分比为21.1%~22.7%,波动小于交叉口间距相等时的20.4%~22.7%.与之类似,P2相序在交叉口间距不等情况下的波动幅度21.2%~23.0%,同样也小于交叉口间距相等时的20.6%~23.0%.
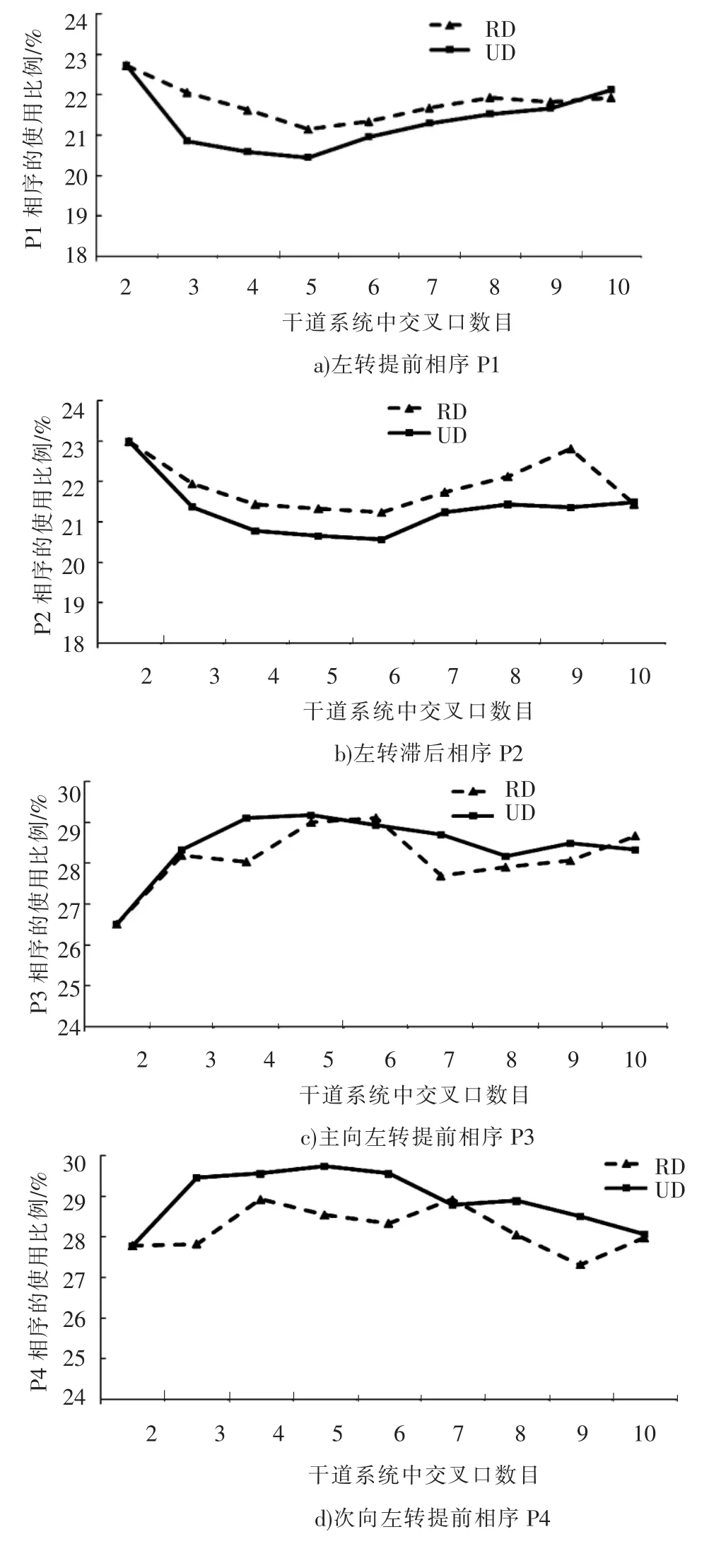
图4 相序使用比例分布
图4c)、d)为P3相序和P4相序使用比例示意图.能够看出这2种相序的使用比例在优化后的干道系统中也较为接近.其中,P3相序使用比例在交叉口间距随机和相等2种情况下的均值分别为28.1%和28.4%.P4相序在上述2种情况下的均值分别为28.2%和28.9%.此外,从上述均值中能够看出当交叉口间距相等时,上述2种相序情况会有更高的使用比例.为了验证上述假设的有效性,对仿真结果进行t检验(见表5).
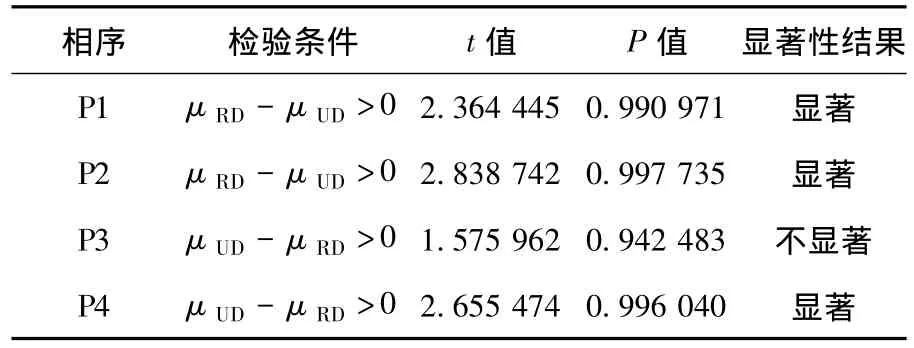
表5 相序使用比例t检验结果
检验结果表明,P4相序在交叉口间距相等情况下的相位使用比例显著高于间距不等的情况.而针对P3相序,尽管在交叉口不等间距时检验结果显示区别不显著,但检验结果仍说明94.2%的情况下等间距交叉口更偏好使用该相序.
此外,对比上述4种相序能够发现,P3、P4的使用比例明显高出P1、P2相序5%以上.这主要是由于P3、P4相序的主路直行相位在调节相位差的过程中能够各自向不同的方向进行调整,而P1、P2相序则需要向同一方向进行调整.
4 交叉口数量对干道系统协调控制的影响
干道系统包含的交叉口数目对绿波带优化有着极为重要的影响.但是这种关系一直未被量化研究,在实际工程应用中也大都以主观推测的方式认为当交叉口目数超过一定限度,干道系统的双向绿波基本无法实现.本文利用绿波利用率、平均优化方案数和无法优化系统百分比3个指标,从不同角度量化分析了交叉口数目对绿波优化的影响,见图5~7.
1)绿波利用率(Attainability)为绿波带宽与双向直行绿信号时长总和的比值,它表示了绿波带宽的使用效率,其计算方法为A=Bmax/(Go,min+Gi,min).
绿波利用率的分析可以看出,随着干道系统每加入一个新交叉口,该系统的绿波优化效率会降低5%左右.图5中交叉口间距不等和相等情况下的仿真数据能够看出,在交叉口数<7时,不等间距交叉口群有着更高的绿波利用率.而当交叉口数>7之后,等间距交叉口群的绿波利用效率会略微高于不等间距交叉口群.这就说明在交叉口数目<7时,且系统中不同的交叉口具有不同的相位条件时,通常情况下认为的等间距交叉口群更容易获得更大的绿波带宽是不成立的.
进一步分析各种交叉口数目情况下绿波利用率的标准差变化,发现相对不等间距交叉口群来说,等间距交叉口群的绿波利用率波动更为明显.这就进一步说明等间距交叉口群在进行绿波优化的过程中,优化结果有着更高的不确定性.
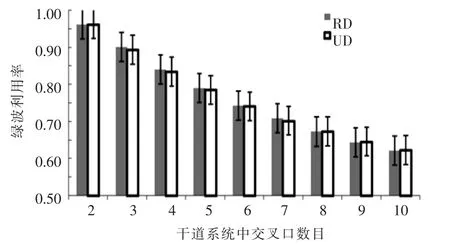
图5 绿波利用率
在对平均优化方案数这一指标进行分析时能够看出,干道系统所包含的交叉口数与其所能提供的优化方案数呈二次正相关关系.拟合结果为


图6 平均优化方案数
当交叉口数<7时,等间距交叉口群能得出更多优化方案.在交叉口数>7以后,不等间距交叉口群有着更高的优化选择.说明当干道系统中包含的交叉口数目越多时,不等间距交叉口群反而更加容易得出优化方案.
对干道系统无法进行优化的百分比进行分析,结果见图7.通过对数据点进行拟合能够发现,干道系统中无法进行优化系统的百分比与系统中交叉口数成二次正相关关系.在拟合过程中,针对不等间距交叉口群和等间距交叉口群的相关系数R2分别等于0.997 0和0.997 5,拟合程度非常接近1,说明拟合曲线对样本数据的拟合非常出色.不等间距系统的拟合曲线位于等间距系统拟合曲线的下方,说明相对于等间距系统,不等间距系统在相同条件下不能进行优化的百分比更低.
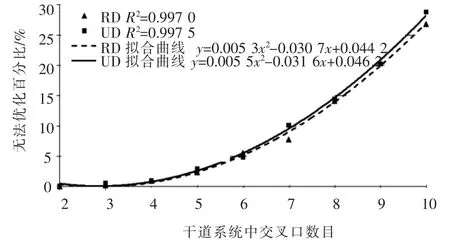
图7 无法优化百分比
从上述拟合曲线可以看出,随着交叉口数的增加,干道系统能进行绿波优化的可能性逐渐降低.本文利用不等间距条件下的拟合公式进一步计算了交叉口数>10的各种场景.进一步分析能够发现,当交叉口数>16后,干道系统能够进行优化的可能性将<0.说明若要对交叉口数>16的干道系统进行绿波优化时,首先需要对交叉口群进行分割,将一个干道系统分为若干子系统再进行进一步的绿波优化.
5 结论
1)为了达到最优的双向绿波方案,主向、次向左转提前相位在实际交通信号配时过程中有更高的使用比例.
2)在进行绿波优化的过程中,等间距交叉口群更偏好使用主向、次向左转提前相位,而不等间距交叉口群则更偏好使用左转提前或左转滞后相位.
3)在交叉口数<7时,且系统中不同的交叉口具有不同的相位条件时,不等间距交叉口群反而更容易获得更大的绿波带宽,且更加容易得到优化配时方案.
4)干道系统包含交叉口数>16后,该干道系统基本无法获得任何双向绿波带.
[1] KOONCE P,RODEGERDTS L,LEE K.Traffic signal timing manual[M].McLean,VA:Federal Highway Adminstration,2008:19-21.
[2] BROOKS W D.Vehicular traffic control:designing traffic progression using a digital computer[M]. Kingston,NY:IBM-Data Processing Division,1965: 135-148.
[3] 全永燊.城市交通控制[M].北京:人民交通出版社,1989:47-52.
[4] 常云涛,彭国雄.基于遗传算法的城市干道协调控制[J].交通运输工程学报,2003,3(2):106-112.
[5] 刘灿齐.城市道路网络交通信号协调控制的优化[J].同济大学学报:自然科学版,2004,32(8):1000 -1004.
[6] 袁二明,涂奉生,蔡小强.基于混合整数规划的相邻交叉路口信号协调控制[J].系统工程,2006,24 (8):32-37.
[7] 李振龙,赵晓华.基于Agent的区域交通信号协调控制[J].武汉理工大学学报:交通科学与工程版,2008,32(1):130-133.
[8] 孙超,徐建闽,丁恒,等.基于模糊控制算法的干道信号协调控制优化[J].交通与计算机,2008,26 (4):55-58.
[9] 万绪军,陆化普.线控系统中相位差优化模型的研究[J].中国公路学报,2001,14(2):99-102.
[10] 刘东,隗卓.近距离交叉口信号配时协调控制方法研究[J].中国人民公安大学学报:自然科学版,2006,3:78-82.
[11] 卢凯,徐建闽.干道协调控制相位差模型及其优化方法[J].中国公路学报,2008,21(1):83-88.
[12] 马楠,邵春福,赵熠.基于双向绿波带宽最大化的交叉口信号协调控制优化研究[J].吉林大学学报:工学版,2009,39(Sup 2):19-24
[13] National Electrical Manufacturers Association.TS 2 -2003[S].Rosslyn,VA:NEMA Standards Publication,2003:96-98.
[14] MORGAN J T,LITTLE J D.Synchronizing traffic signals for maximal bandwidth[J].Operations Research,1964,12:896-912.
[15] LITTLE J D.The synchronization of traffic signals by mixed-integer linear programming[J].Operations Research,1966,14:568-594.
[16] MESSER C J,WHITSON R N,DUDEK C L,et al. A variable-sequence multiphase progression optimization program[J].Highway Research Record,1973,445:24-33.
[17] TIAN Z,MANGAL V,LIU H.Effectiveness of leadlag phasing on progression bandwidth[J].Transportation Research Record,2008,2080:22-27.
