直接蒸发式三套管蓄能换热器的蓄冷特性

牛福新，倪 龙，姚 杨，马最良

(哈尔滨工业大学市政环境工程学院，150090哈尔滨，fuxinniu@163.com)

随着经济的快速发展，商业用电大幅度增加，每年增加幅度约10%～20%.近年来的总装机容量不断增长，截至2008年底全国发电装机容量达到7.1亿kW［1］.为缓解高峰电力严重不足，蓄冷空调是电力需求实现“移峰填谷”最有效手段之一.目前，国内外蓄冷技术主要集中在对冰蓄冷的研究与设备开发［2-3］，利用水的相变蓄冷，相变温度为0℃，因此要求制冷剂蒸发温度较低，影响机组效率，而且该系统只能蓄冷，不能蓄热，有时为了蓄热不得不采用另外一套装置，系统复杂.为此，本文采用相变温度为6℃的有机相变材料，结合三套管蓄能换热器，能同时解决空调系统夏季常规冷机蓄冷、冬季太阳能蓄热、将多源热泵与蓄能有机结合.通过三套管蓄能换热器可以组成三套管蓄能型太阳能与空气源热泵集成系统［4］.虽然众多研究者对相变换热器开展了深入研究［5-11］，但由于三套管蓄能换热器结构的特殊性，其换热机理研究还未见报道.

1 三套管蓄能换热器结构

三套管蓄能换热器单个换热单元见图1，其内管为制冷剂，中间层为相变蓄能材料，外管为水，通过制冷剂/相变蓄能材料换热实现夏季蓄冷，冬季取热;而相变蓄能材料/水之间的换热实现夏季释冷，冬季蓄热.冬季蓄热的来源可以是太阳能等低位热源，这样通过管路转换，三套管相变蓄能器既是夏季供冷工况的蓄冷装置，也是冬季供热工况的蓄热装置，简化了系统.相变材料的选择要满足蓄冷和蓄热的要求.一般而言，冬季设计条件下的太阳能集热低温热水为15～20℃，夏季供冷设计水温为8～10℃，选择有机相变材料RT6，其相变温度为 6 ℃，导热系数为0.4 W/(m·K)，蓄热量在 1～11℃范围内为183 kJ/kg.

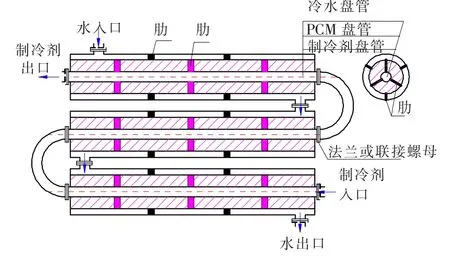
图1 三套管蓄能换热单元示意

2 三套管蓄能换热器数学模型

2.1 外层水侧的数学模型

外层水的任一微元可以建立方程

2.2 相变材料层的数学模型

根据圆柱形对称的特点，即各个半径方向上温度场相同，因此圆柱形蓄热体的温度场分布可看作是二维的，即沿径向(圆柱半径方向)和轴向(流体流动方向)，取环形的微元体，见图2.

根据焓法模型的微分方程，建立PCM微元体能量控制方程:

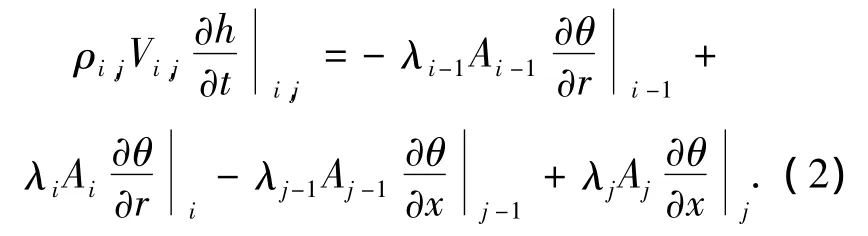
将焓转换为温度，其转化关系式为

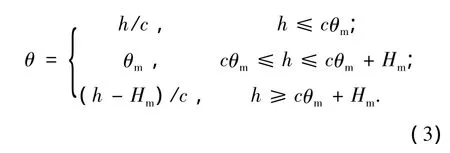
相变的影响包含在式(3)中，其中θm为相变温度，因为焓h中也包含了相变潜热Hm.

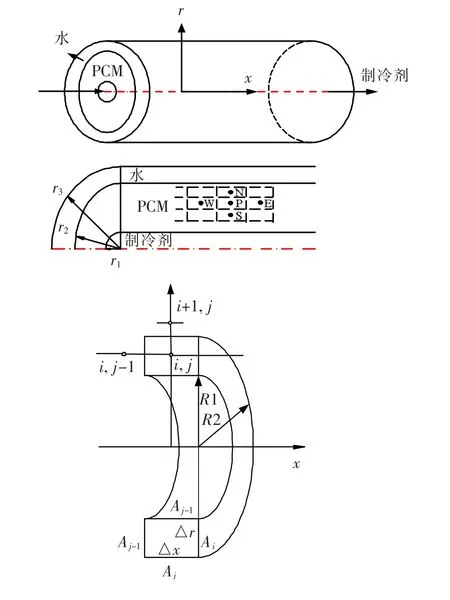
图2 蓄热单元及微元体示意

2.3 制冷剂侧的数学模型

一般来说，制冷剂在蒸发器内流动换热主要经历2个区段，即两相区及单相区(过热区).由于在蒸发器内制冷剂主要呈环状流的形式流动，故本文对于翅片管蒸发器两相流仅以环状流进行建模.在建立节点动态模型之前拟作如下假设:

1)制冷剂沿水平管作一维流动;

2)两相流在同一流动截面上气相和液相的压力相等;

采用哈尔滨工业大学研制的钻取采样试验平台开展系统级模拟钻进试验，如图11所示。锁合随动式限幅机构与取芯钻具的安装状态如图12所示。在钻取采样试验中，钻具在钻进过程中产生了一定弯曲变形，它与主支撑架限幅环之间存在磨损，限幅机构在此工况下保持正常锁定。当取芯钻具加载到限幅机构预定钻深处时，钢球顺利释放，限幅机构和取芯钻具实现随动钻进，满足钻取采样工作阶段的功能需求。

3)制冷剂侧能量方程中忽略动能和势能的影响;

4)忽略管壁的轴向导热;

5)不计制冷剂重力的影响;

6)在蒸发器的分布参数模型中，不考虑压降.

2.3.1 两相区

由于蒸发器内两相流处于环状流已经达成共识，仅以环状流对蒸发两相流进行建模.

环状流动的主要特征是气相流在管内流动，而液膜以不同的速度环绕于管内壁上，同时有少许的液滴被夹带到气流中.随着制冷剂干度的减小，液膜的厚度逐渐增加，而气相流动截面积逐渐减小.

将蒸发器划分为若干微元，对于任一微元可建立方程

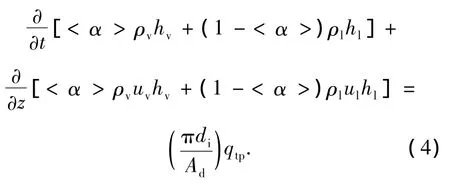
其中

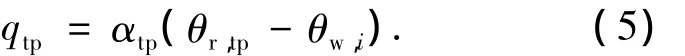
式中:＜α＞为空隙率［12］，表示在控制单元内气相占的体积份额;ρv，ρl为制冷剂的气、液相密度，kg/m3;uv，ul为制冷剂的气、液相流速，m/s;Ad为管道截面积，m2;hv，hl为制冷剂的气、液相焓，kJ/kg;qtp为两相热流密度，W/m2;di为管内径，m;αtp为两相对流换热系数，W/(m2·℃);θr，tp为微元体制冷剂进出口平均温度，℃;θw，i为管内壁温度，℃.

2.3.2 单相区(过热区)

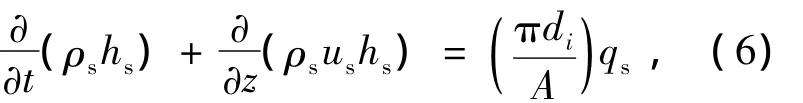
其中

式中:ρs为单相制冷剂密度，kg/m3;us为单相制冷剂流速，m/s;hs为单相制冷剂的焓，kJ/kg;qs为单相热流密度，W/m2;αs为单相对流换热系数，W/(m2·℃);θr，s为微元体单相制冷剂进出口平均温度，℃.

管壁部分能量守恒方程

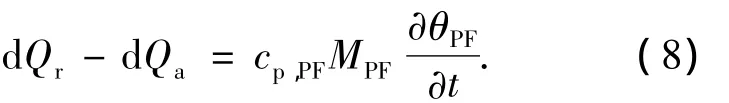
式中:dQr为制冷剂吸收的热量，kW;dQa为PCM放出的热量，kW;cp，PF为管子和肋片的平均比热，kJ/(kg·℃);MPF为微元管子和肋片的平均质量，kg;θPF为管子和肋片的温度，℃.

考虑到管子与肋片材质的不同，采用平均比热

3 模拟结果及分析

模拟条件如下:压缩机型号AEZ3440E，制冷量980 W，输入功率250 W;三套管相变层厚度为6 mm，长6 m.图3是模拟过程中，制冷剂蒸发温度的变化情况.可以看出，蒸发温度整体变化是逐渐降低的，随着蓄冷的进行，PCM释能过程也是逐步进行的，PCM的温度逐渐降低，制冷剂蒸发温度也随之降低.初始阶段蒸发温度下降的较快，是由于这个阶段PCM处于液相显热蓄冷阶段，其显热蓄冷能力有限，故温度下降很快.随后蒸发温度下降逐渐放缓，PCM主体处于相变蓄冷阶段，温度变化小，由于相变材料的特性，在低温部分相变潜热是逐步释放出来的，因此在蓄冷过程中，蒸发温度的下降都是比较平缓的，相变潜热是被逐步释放出来的，到蓄冷完成，蒸发温度降低到-2℃左右.

图3 蓄冷模式下蒸发温度变化曲线

图4为入口处PCM径向A、B点温度变化曲线(A、B两点为PCM盘管入口处，沿径向上贴近制冷剂侧和水侧的两点)，由图可知，蓄冷模式下，PCM的初始温度为14℃，当制冷剂进入三套管蓄能换热器之后，A、B两点的温度开始下降.开始的阶段内温度下降较快，这是由于PCM处于显热蓄冷状态.A点由于紧贴近制冷剂管壁，微元容积较小，因此潜热蓄冷时间非常短暂，温度下降很快，仅在蓄冷进行4～6.5 min时候处于相变区间.此时B点仍然处于液态显热蓄冷状态.由于B点处于环形PCM的外边界，A点进入两相区直至固相区后，换热热阻增大，因此7.2 min后B点才进入潜热蓄冷阶段.此后，B点处在潜热蓄冷状态一直持续到18 min，与此对应时段A点已经处于显热蓄冷阶段，但是温度下降很缓慢，这主要是由于沿径向PCM各个节点的热量都是经由A点传递给制冷剂流体的，所以A点在这个过程中变化也很缓慢.在18 min后B点也进入显热蓄冷阶段，此时三套管蓄能换热器入口处径向已经全部为固态，这个阶段PCM的传热系数和热容量均显著降低，因此温度下降很快，曲线的斜率也很大.

图5为C、D两点的温度变化曲线(C、D两点为PCM盘管出口处沿径向上贴近制冷剂侧和水侧的两点)，PCM的初始温度为14℃，蓄冷模式开始后，C、D两点的温度开始下降，但是相对于A、B两点的下降趋势要缓和一些.C点在7.3～11 min时处于相变区间，开始相变的时间相较于A点延迟了3.3 min，在相变区间持续的时间也由A点的2.3 min延长至3.7 min.D点在11.5 min时进入相变区间，相较于B点延迟了4.3 min，结束相变的时间与B点相比较延迟了5 min.在系统开始运行23 min后，三套管蓄能换热器出口径向也全部变为固态，进入显热蓄冷区间.

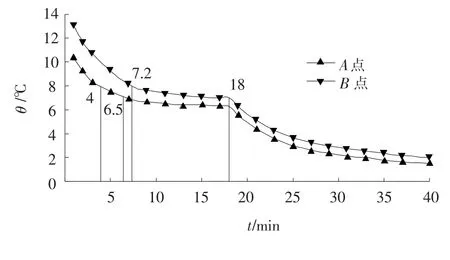
图4 入口处PCM径向A、B点温度变化曲线

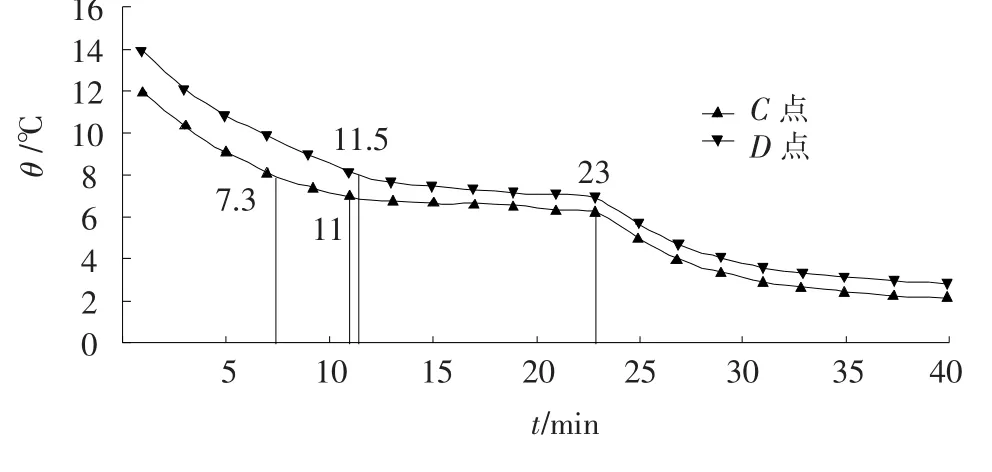
图5 出口处PCM径向C、D点温度变化曲线

4 与冰蓄冷比较分析

与冰蓄冷相比，高温相变材料蓄冷的相变温度为6℃，要求的蒸发温度要高于冰蓄冷时的蒸发温度，因此提高了机组的效率，图6为冰与高温相变材料相变蓄冷时对应的蒸发温度及COP(能效比)的对比关系.相变蓄冷过程中，随着蓄冷过程的进行，温度不断降低且变化趋于平稳，与之对应的COP值也随之下降.冰蓄冷蒸发温度变化平缓，约为-10℃，高温相变蓄冷平均蒸发温度为0.4℃.冰蓄冷COP平均值为3.2，高温相变蓄冷平均COP值为3.95，比冰蓄冷提高了近25%，具有明显的节能效果.

如选用同一台压缩机(型号:YZG-25RT1)进行冰蓄冷与相变蓄冷时，不同室外温度运行工况时机组性能分析如图7～9所示.图7给出了冰与相变蓄冷COP随室外温度的变化曲线，随着室外温度的升高，COP值不断下降，当室外温度为15℃时，冰蓄冷COP值为3.7，而相变蓄冷COP值达到了6.6.图8给出了冰与相变蓄冷制冷量随室外温度的变化曲线，随着室外温度的升高，制冷量不断下降，但下降速率变化不大.冰蓄冷平均制冷量为 1.7 kW，相变蓄冷平均制冷量为2.4 kW.图9给出了冰与相变蓄冷耗功随室外温度的变化曲线，随着室外温度的升高，耗功不断升高.其中相变蓄冷耗功变化速率高于冰蓄冷，当室外温度达到30℃时，2种蓄冷方式耗功相等.

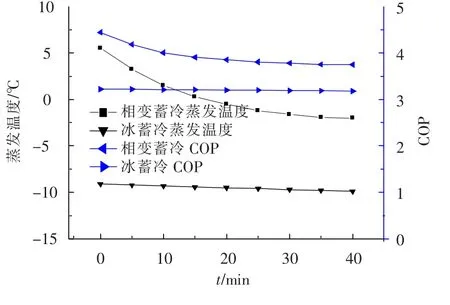
图6 冰与高温相变材料相变蓄冷时对应的蒸发温度及COP

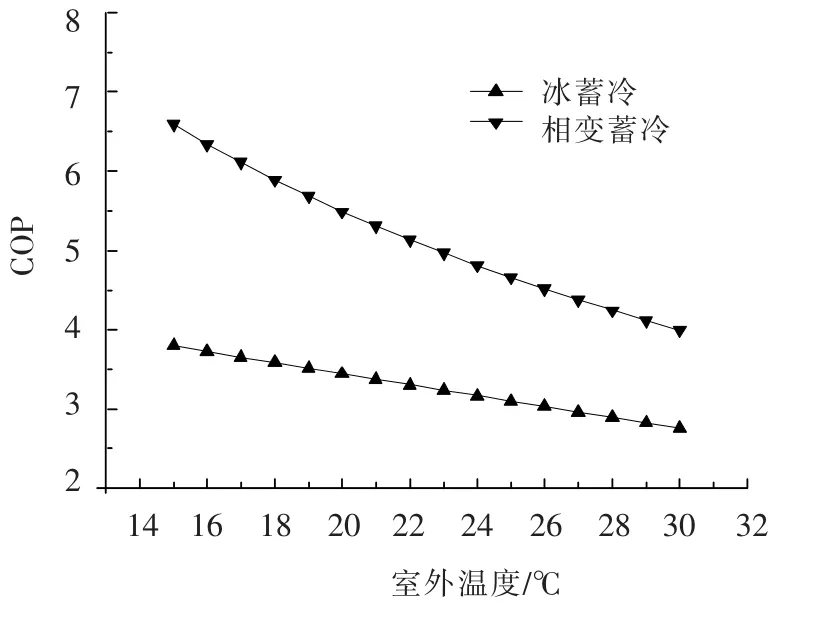
图7 冰与相变蓄冷COP随室外温度的变化曲线

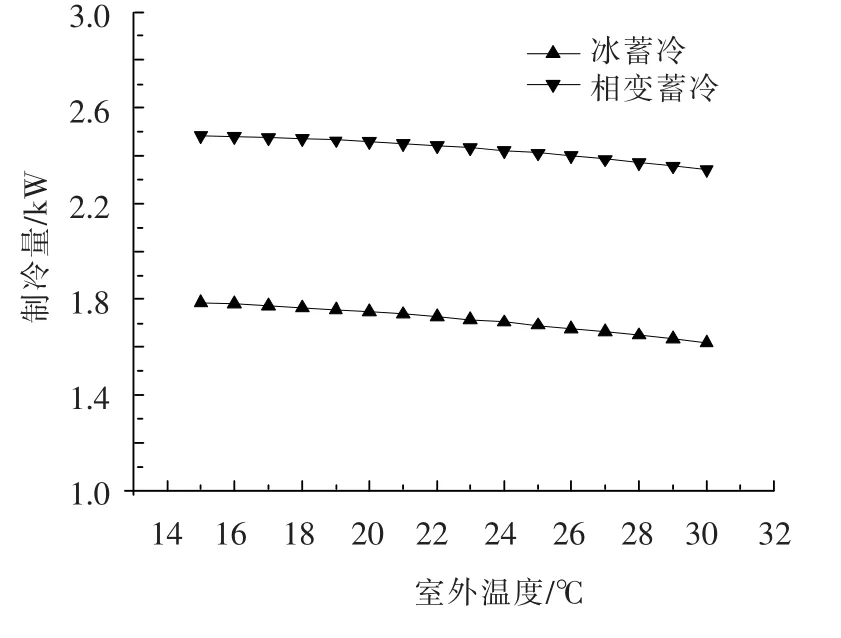
图8 冰与相变蓄冷制冷量随室外温度的变化曲线

图10给出了相同制冷能力3 kW下，冰与相变蓄冷耗功随室外温度的变化曲线.随着室外温度的升高，耗功不断升高.其中冰蓄冷功耗高于相变蓄冷，室外温度从5℃一直到30℃，冰蓄冷功耗与相变蓄冷功耗之差基本保持不变，为0.33 kW.与冰蓄冷相比，相变蓄冷功耗节能率达36%.

图9 冰与相变蓄冷耗功随室外温度的变化曲线

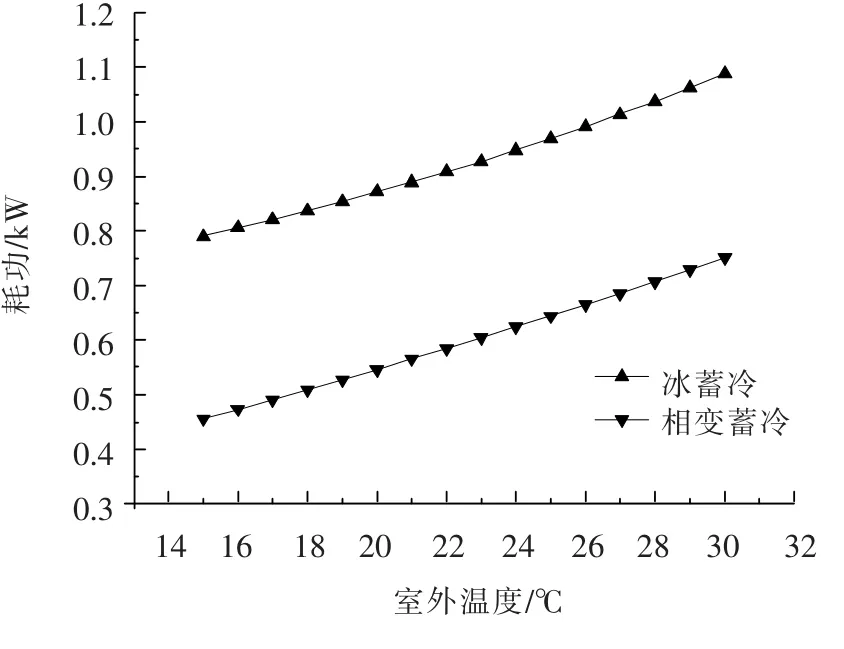
图10 相同制冷能力时冰与相变蓄冷耗功随室外温度的变化曲线

5 结语

为解决单一节能技术的局限性，提出了三套管蓄能换热器，该蓄能换热器可以与空气源、太阳能热泵组成集成系统.建立了三套管蓄能换热器的数学模型，蓄能换热器两侧发生相变，数学模型复杂，编制了系统仿真程序，模拟了三套管蓄能换热器直接蒸发蓄冷动态特性.结果表明:相变蓄冷过程中，蒸发温度不断下降且变化趋势平稳，平均蒸发温度为0.4℃.通过与传统的冰蓄冷比较，平均蒸发温度提高了10℃左右，COP值提高了近25%，相同制冷能力下相变蓄冷功耗比冰蓄冷耗功节省36%，具有良好的节能效果.

［1］周小谦.我国电力发展与西北电力展望［J］.电网与清洁能源.2008，24(3):3-10.

［2］白莉，迟铭书.我国冰蓄冷空调技术现状及趋势研究［J］.吉林建筑工程学院学报，2008，25(2):77-81.

［3］HENZE G.Guidelines for improved performance of ice storage systems［J］.Energy and Buildings，2003，35 (2):111-127.

［4］杨灵艳，倪龙，姚杨，等.蓄能型太阳能与空气源热泵集成系统运行模式［J］.煤气与热力，2009，29(1): 1-4.

［5］方贵银.蓄冷平板相变换热器凝固传热特性研究［J］.低温与特气，1999，24(3):23-27.

［6］CHEN Hujun，CHEN Shili.Optimization of an icestorage air-conditioning system using dynamic programming method［J］.Applied Thermal Engineering，2005: 461-72.

［7］LEMORT V.A numerical comparison of control strategies applied to an existing ice storage system［J］.Energy Convers Manage，2006，47:3619-31.

［8］LI Wensheng，CHEN Yiting，WU Tinghua.Optimization for ice-storage air-conditioning system using particles warm algorithm［J］.Applied Energy，2009，86: 1589-1595.

［9］YOHANIS Y G，POPEL O S.A simplified method of calculating heat flow through a two-phase heat exchanger［J］.Applied Thermal Engineering，2005，25:2321-2329.

［10］DIZA G.Controllability of cross-flow two-phase heat exchangers［J］.International Journal of Heat and Mass Transfer，2007，50:4559-4567.

［11］LACROIX M.Use of a phase change material to prevent frosting in a compact cross flow air exchanger［J］.Energy Conversion and Management，2001，42: 1277-1296.

［12］姚杨.空气源热泵冷热水机组冬季结霜工况的模拟与分析［D］.哈尔滨:哈尔滨工业大学.2002.