多台数控机床的时间截尾可靠性评估
2011-03-12王智明杨建国王国强张根保
王智明,杨建国,王国强,张根保
(1.上海交通大学机械与动力工程学院,200240上海,wangzm301@sjtu.edu.cn; 2.重庆大学机械工程学院先进制造技术实验室,400030重庆)
在数控机床的可靠性评估中,平均故障间隔时间(tMTBF)、给定时间的可靠度R(t)和一定可靠度下的工作时间t(R)是评估机床可靠性的重要指标之一.可靠性试验是可靠性评估的基础,一般常采用多台定时截尾试验[1-2].
分布模型的选择是评估的难点和关键.常见的分布模型有指数分布和Weibull分布,其选择的方法是先假设故障间隔时间(tTBF)服从某一分布,随后用K-S或χ2检验进行检验[3],但有时会出现2种分布均被通过的情况[4];对于可线性化的分布模型,可用最小二乘法求解模型,并用相关系数进行检验[5],但该方法所得模型并非最优;另外,还有其他选择模型的方法,如:综合法[3]、误差面积比[4]、灰关联[6]、神经网络[7]等方法.但对于少样本数据,上述方法所得模型精度一般较低.在机床可靠性评估中,参数估计多局限于参数的点估计,对于参数区间估计的报道则较少.
本文基于AIC、BIC信息准则优选tTBF模型和参数,给出了tTBF模型参数和可靠性指标的点估计,用 Fisher信息矩阵法给出了模型参数及R(tMTBF)、t(0.9)等可靠性指标的区间估计.最后用蒙特卡洛法(MC)提高了区间估计的精度.
1 基于AIC、BIC信息准则的模型和方法选择
1.1 模型选择
数控机床时间截尾数据通常为不完全数据,其中包含右删失数据.设某次试验投入k台机床,所得数据为t=(ti,tcj)(i=1,2,…,n;j=1,2,…,k),其中ti为失效数据,tcj为截尾数据.一般每台机床有一个截尾数据,且不相等.设截尾数据的概率密度和可靠度分别为f(t;θ)、R(t;θ),则用极大似然法(MLE)优选模型时,其对数似然函数为

令

则可得参数的估计值^θ.
不同模型对试验数据信息反映的准确性各异,其中,只有对数据拟合度好、参数少、形式简单的模型才是最佳模型.AIC信息准则将K-L距离和极大似然方法相结合,并利用了似然估计性质[8-9],其形式如下:
AIC=-2(maximum log likelihood)+2m. BIC信息准则[10-11]是另一种模型选择的有效方法之一,其形式如下:
BIC=-2(maximum log likelihood)+m×ln(n).其中m是参数数量,n是观测数据数.可见,BIC对增加的参数加上更大的惩罚项m×ln(n).因此,BIC更有可能选择参数少的模型.AIC、BIC作为模型选择的有效方法之一,其值越小者模型越好.
故障间隔时间分布模型一般为指数分布或Weibull分布,因此,以指数分布、Weibull分布或其他分布作为备选分布模型,用MLE法分别求取最大似然函数值,最后得到AIC、BIC值,该值最小者即为所求最佳模型.
1.2 方法选择
常见的估计参数的方法有最小二乘法(LSM)和MLE法.其中,LSM根据因变量的不同可分X方向秩回归(RRX)和Y方向秩回归(RRY)[12].
Weibull模型可经对数变换线性化,然后用LSM求解.对于不完整数据可用Johnson法得到不完整数据中失效数据的失效顺序号,再按中位秩估计得到相应的可靠度[13].Weibull模型用MLE法估计参数时,所得极大似然估计方程没有封闭形式,可用迭代法解之.为了使其快速收敛,初值可取LSM所得估计值.最后用AIC、BIC准则优选最佳参数估计方法.
2 参数及可靠性指标的区间估计
2.1 参数的区间估计
通常在大样本情况下,极大似然估计量是渐进正态分布的.在小样本情况下,参数的对数更接近正态分布.所以,根据渐近正态原理有

进而可得参数θ的估计区间值如下:

其中,var(^θ)为估计参数的方差,zα/2为置信度为1-α的正态分布的分位数.因此,若求得参数的方差,即可得其估计区间.参数的方差可用Fisher信息矩阵法(FM)解决[14-15],即参数方差矩阵为Fisher信息矩阵的逆.为了便于说明,下面以两参数Weibull分布为例.
设时间截尾Weibull分布的失效数为n,截尾数为k,则由式(1)知其对数似然函数为
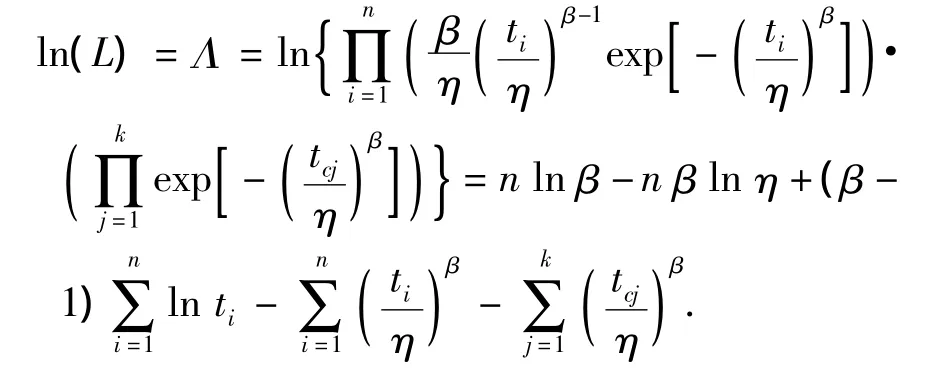
其中,β为形状参数,η为尺度参数,均大于零,所以
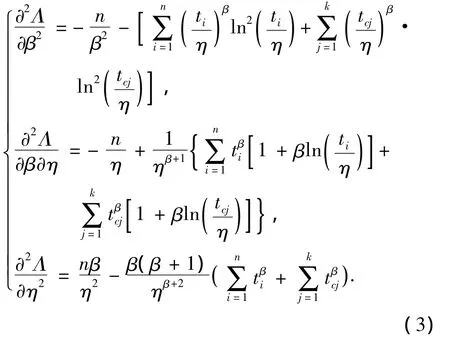
由Fisher信息矩阵法知

2.2 可靠性指标的区间估计
在获得模型的参数估计值后,易得其点估计,平均故障间隔时间(tMTBF)、给定时间的可靠度R(t)和一定可靠度下的工作时间t(R)计算公式如下:
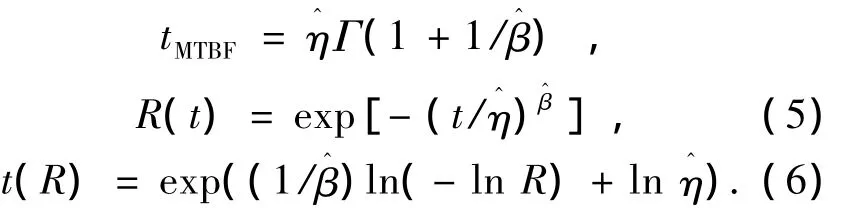
2.2.1 给定时间可靠度R(t)的区间估计
在Weibull分布中,设T=ln t,则T服从极小值分布,其可靠性函数为

μ、σ为该函数参数.设μ=ln η,σ=1/β,u= β(ln t-ln η),则极小值分布可靠性函数可变换为Weibull分布可靠性函数
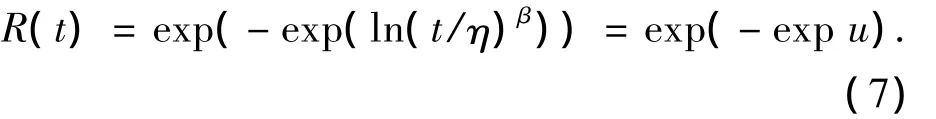
所以,若u的置信区间已知,便可得出R(t)的置信区间.u的置信区间为

其中,

至此,由式(7)可得出给定时间可靠度的置信区间估计
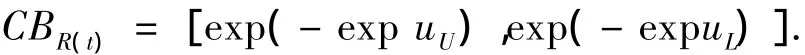
2.2.2 一定可靠度下的工作时间t(R)的区间估计
在式(6)中,令
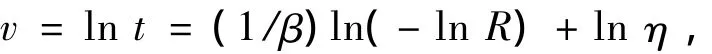
则
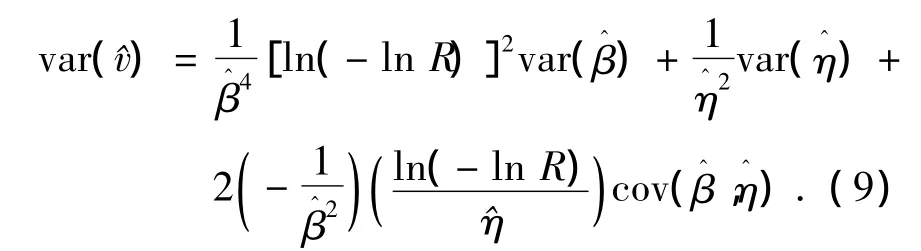
所以,v的置信区间为 CBv=[vL,vU] =,最后得到t的置信区间为
3 案例分析
数据来源于文献[1],该文给出了10台加工中心的不完整数据30个,其中失效数据20个,时间截尾数据10个,属于小样本数据.具体为: 176.00,248.00,10.50,472.00,45.00,39.00,209.33, 261.25, 510.00,120.00, 224.00,267.50, 32.00, 50.00, 138.50, 398.00,478.00,353.00,348.00,137.06,332.50*,84.00*, 267.00*, 165.00*, 283.16*,700.00*,562.00*,387.00*,383.00*,1.50*(带*号者为时间截尾数据).
3.1 模型选择
以指数分布、Weibull分布作为备选分布模型,用MLE法求解,所得结果如表1所示.

表1 模型选择结果
从表1可见,2参数Weibull分布的AIC、BIC值均较小,所以选取2参数Weibull分布作为时间截尾TBF可靠性评估模型.
3.2 方法选择
2参数Weibull分布的可靠性函数如式(5),线性化后令y=ln[-ln(R(t))],x=ln(t),则
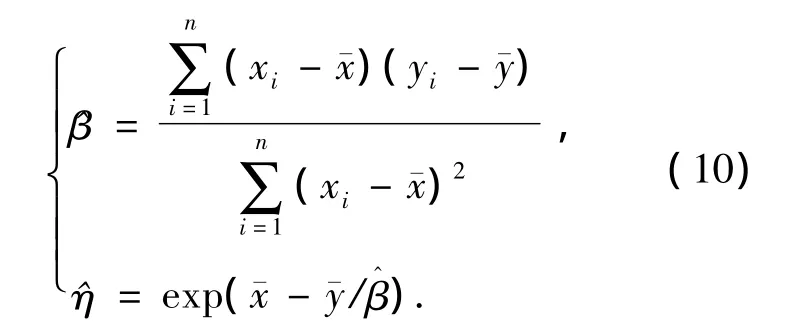
R(t)可用如下中位秩公式估计:

对于时间截尾数据,失效数据的失效顺序ri可用Johnson法估计,公式如下:
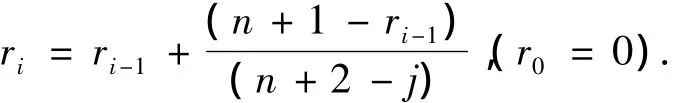
得出ri后代替式(11)中的i即可得截尾数据的可靠度Ri.用LSM方法中的RRY估计参数时,由式(10)知β=1.024 4,η=407.942 6.为了选取最佳参数,还可用RRX和MLE法估计,结果如表2所示.由表2可见,当2参数Weibull分布分别用RRX、RRY、MLE 3种不同方法估计参数时,MLE方法所得AIC、BIC最小,模型精度最高.

表2 方法选择结果
至此,选择MLE方法得模型参数、机床的tMTBF及该时刻的可靠度R(tMTBF)以及可靠度为0.9的工作时间t(0.9)的点估计分别如下:β= 1.200 9,η =376.989 3,tMTBF=354.545 9,R(tMTBF)=0.395 0,t(0.90)=57.88.
3.3 参数及可靠性指标的区间估计
由式(3)、(4)知参数的协方差矩阵为
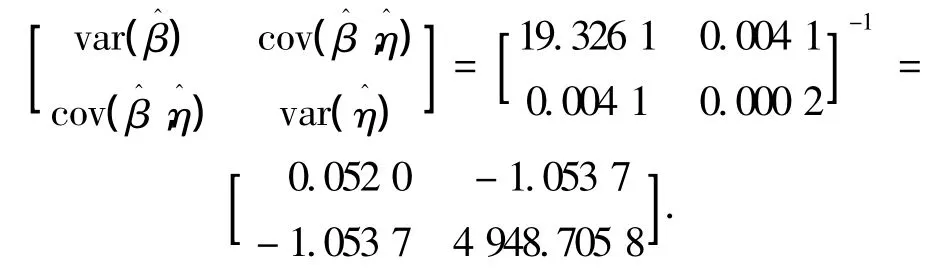
由式(2)得参数β、η的置信度为0.95的置信区间分别为[0.827 7,1.742 3]、[261.515 2,543.451 7].另外,由式(8)得u的方差后知其估计区间为CBu=[-0.511 5,0.365 1],其中方差var(u)=0.050 0.同样,由式(9)得v的方差后可得其估计区间,最后得出R(tMTBF)和t(0.9)的估计区间分别为CBR(t)=[0.236 8,0.549 0],CBt(0.9)=[26.91,124.47].
由估计区间结果来看,该区间太大,估计精度较低,所以有必要提高区间估计的精度.事实上,上述区间估计采用渐进正态分布原理,适合于大样本.对于小样本数据,其估计精度一般较低.通常将样本单位数不少于30个的样本称为大样本,不及30个的称为小样本.数控机床的故障数据一般为少样本数据,因此,对于少样本数据可用模拟抽样的方法来扩大样本容量,从而提高区间估计精度.
3.4 MC仿真抽样
2参数Weibull分布的tTBF的抽样公式为

r为(0,1)区间上均匀分布的随机变量.取样本容量 N分别为 500、1 000、2 000、5 000、8 000、10 000,其参数和可靠性指标抽样区间估计分别如图1、2所示.从图可见,样本容量为8 000和10 000时的估计结果已经很接近,因此停止抽样,并取容量为10 000时的抽样结果为最终估计值.其结果如表3所示.从表3可以看出,估计区间均已大大减少.其中,t(0.9)、R(tMTBF)区间长度分别减少93.21%、95.07%.

图1 参数β、n的区间仿真

图2 可靠性指标R(tMTBF)、t(0.9)的区间仿真

表3 样本容量为10 000时的区间模拟抽样结果
4 讨论
1)在Weibull分布模型中,当形状参数β=1时,Weibull分布就转换为指数分布,模型处于浴盆曲线的偶然失效区;当β<1或β>1时,则模型对应于浴盆曲线的早期失效或耗损失效.可见本案例中的加工中心处于耗损失效期.因此,Weibull分布模型因其灵活性作为故障间隔时间的分布模型而广泛应用于NC机床的可靠性分析中.在2-Weibull模型的参数估计中,MLE法较之LSE法有更高的估计精度.这是因为LSE法在对数变形代换过程中改变了因变量的形态,变形后因变量残差平方和最小并不能保证变形前因变量残差平方和最小,同时,用Johnson法对不完整数据中的失效数据排序时,只考虑了其失效顺序而没有考虑截尾数据的相对大小.换言之,对于不同大小的截尾数据,当用Johnson法分析时,失效数据可能有相同的失效顺序.当截尾数据较多时,只拟合重新排序后的失效数据(本案例只有20个失效数据)的LSE法的评估精度自然会受到影响.MLE适用于完整数据和不完整数据,精度较之LSE法有较好的评估效果.但LSE法的评估结果可作为MLE法中迭代计算模型参数的初值,因此,使用MLE法时可结合LSE法而达到快速收敛的目的.本文所提方法虽然是针对时间截尾的,但仍适用于定数截尾实验.当采用定数截尾时,各有关公式中tcj=0.
5 结论
1)在NC机床的可靠性评估中,对不完整数据可结合LSE法的结果,优先选用MLE法.
2)AIC、BIC信息准则结合了MLE的计算结果和模型的简约原则,是机床可靠性评估中优选模型和模型参数的有效方法.
3)评估模型参数和可靠性指标的区间时,对于大样本数据,可采用基于渐进正态分布的FM法,但当样本数据较少时,可用MC仿真法扩充样本容量,提高区间估计精度.
[1]DAI Yi,ZHOU Y F,JIA Y Z.Distribution of time between failures of machining center based on type I censored data[J].Reliability Engineering and System Safety,2003,79:375-377.
[2]张海波,贾亚洲,周广文.数控系统故障间隔时间分布模型的研究[J].哈尔滨工业大学学报,2005,37 (2):198-200.
[3]WANG Yiqiang,YAM R C M,ZUO Mingjian.A multicriterion evaluation approach to selection of the best statistical distribution[J].Computers&Industrial Engineering,2004,47:165-180.
[4]张英芝,申桂香,贾亚洲,等.数控车床故障分布规律及可靠性[J].农业机械学报,2006,37(1):156-159.
[5]ZHANG Haibo,JIA Yazhou,ZHOU Guangwen.Time between failures model and failure analysis of CNC system[J].Journal of Harbin Institute of Technology (New Series),2007,14(2):197-201.
[6]张英芝,贾亚洲,申桂香,等.数控机床故障分布的灰关联分析[J].农业机械学报,2004,35(6):195-197.
[7]王金武,刘家福,许仲祥.履带式拖拉机可靠性与维修性的分析[J].农业机械学报,2004,35(4):81-83.
[8]AKAIKE H.Information theory and an extension of the maximum likelihood principle[C]//Proc Second Int Symp on Information Theory.Budapest:Akademiai Kiado,1973:267-281.
[9]SAYAMA S,SEKINE M.Weibull distribution and K-distribution of sea clutter observed by X-band radar and analyzed by AIC[J].IEICE Transactions on Communications,2000,E83B(9):1978-1982.
[10]SCHWARZ G.Estimating the dimension of a model[J].Ann Statist,1978(6):461-464.
[11]ADRIAN E,RAFTERY.Bayes factors and BIC:comment on"a critique of the bayesian information criterion for model selection"[J].Sociological Methods Research,1999,27(3):411-427.
[12]ZHANG L F,XIE M,TANG L C.A study of two estimation approaches for parameters of Weibull distribution based on WPP[J].Reliability Engineering and System Safety,2007,92:360-368.
[13]JOHNSON L G.Theory and technique of variation research[R].New York:Elsevier Publishing Co,1964.
[14]SANGUN P,BALAKRISHNAN N,GANG Zheng. Fisher information in hybrid censored data[J].Statistics and Probability Letters,2008,78:2781-2786.
[15]ESCOBAR L A,MEEKER W Q.The asymptotic equivalence of the fisher information matrices for type I and type II censored data from location-scale families[J]. Communications in statistics theory and methods,2001,30(10):2211-2225.
