融合图像局部能量和梯度的水平集分割方法
2011-03-12包立君刘宛予浦昭邦
包立君,刘宛予,浦昭邦
(哈尔滨工业大学HIT-INSA中法生物医学图像联合研究中心,150001哈尔滨,baolij@gmail.com)
水平集方法易于处理零水平集拓扑结构的变化,易于扩展,对于结构复杂的图像和多目标图像的分割表现良好,常用于生物医学图像的分割[1-2].水平集分割方法可分为基于边缘信息的活动轮廓模型和基于区域的水平集模型.基于边缘的活动轮廓模型[3-6]依赖于图像的边缘信息,分割存在裂缝和缺口的图像不会产生边缘断裂.但当图像的目标与背景对比度不足,边界模糊或噪声较强时,这类方法会导致水平集演化抖动或从弱边界泄露.基于区域的水平集模型[7]将边缘信息与全局同质区域信息相结合,适用于边缘模糊或边缘不连续的情况,并对噪声具有一定的抑制作用;但其分割灰度不均匀图像时,会将与背景相似的目标区域错分为背景.研究者们相继提出各种改进模型[8-10],但这些模型存在能量函数依靠全局特征的不足.Li提出了一种基于图像局部能量最小化的变分水平集方法[11],这里简称RSF (region-scalable fitting)算法.该方法根据图像局部灰度信息提出了局部能量项,将其作为水平集的外部驱动能量,更适用于分割灰度不均匀图像.但是,受零水平集初始轮廓的影响,局部能量项会出现计算偏差,使得算法的稳定性受到限制,并且算法的收敛速度和水平集的初始化方法有待进一步提高.
本文将图像的梯度信息和局部能量相结合,提出了一种基于局部能量和梯度敏感性的自动初始化水平集算法.梯度敏感项依据图像特征,自适应地确定对水平集的驱动方向.该能量函数能够矫正由局部能量项计算偏差导致的演化错误,提高算法的稳定性,加快了水平集的演化.并且,采用图像的区域极值初始化灰度拟合值,不需要交互式的初始化,提高了算法的效率.
1 RSF算法
RSF算法是一种基于区域的水平集分割方法.设定图像域为Ω∈R,已知灰度图像I,闭合轮廓线C将图像域划分为外部区域Ω1和内部区域Ω2.符号距离函数u初始化为:曲线C(零水平集)处u= 0,曲线C外部区域为Ω1:u=c0,内部区域为Ω2: u=-c0,c0=2.RSF算法的能量泛函定义为

式中:L(u)是弧长约束项,v、μ为权值;P(u)是自适应的距离保持函数,避免了水平集演化过程中需重新初始化带来的繁杂计算[6,11];ξ(u,f1,f2)是水平集演化的主要驱动能量,是图像域中各点的局部能量项ξx(u,f1(x),f2(x))在图像域的积分.局部能量项表征了图像域的局部灰度值与相应的灰度拟合值f1(x)和f2(x)的近似度,其水平集函数定义为

式中,λi是权系数(通常取λ1=λ2),fi(x)是点x相对区域Ωi的灰度拟合函数,y是以x为中心的局部图像域中任意点的坐标,I(y)表示点y的灰度值.局部图像域的尺度为σ,由高斯核函数Kσ定义[11].Hi(u)为Heaviside函数,且H1(u)= H(u),H2(u)=1-H(u).
从式(1)的欧拉-拉格朗日方程解得使ξx(u,f1(x),f2(x))最小化的灰度拟合函数fi(x)为

给定中心点x,在轮廓线C演化到实际目标边界且f1(x)和f2(x)是C两侧区域Ω1和Ω2的最优逼近时,ξx(u,f1(x),f2(x))取得最小值.
灰度拟合函数fi(x)是u的函数,因此轮廓线位置直接关系到fi(x)的计算,进而影响ξx(u,f1(x),f2(x))的取值,从而水平集的演化对初始轮廓敏感.初始轮廓选取的不适当往往会导致水平集收敛所需的迭代次数增加,甚至最终不能收敛到目标边界.特别当初始轮廓线离目标边界较远,或者分割多目标图像时,局部能量项的计算易出现偏差,使得图像域中本应属于同一个区域(Ω1和Ω2)的点被错误分割到不同区域.
另一方面,局部能量项在零水平集附近且图像灰度不均匀的区域具有很强的驱动力.然而,在距离零水平集较远的目标边界处f1(x)≈f2(x),局部能量项的驱动力较弱.同样,在图像灰度均匀的区域f1(x)≈f2(x),局部能量项的驱动力也很弱,水平集演化缓慢甚至会停止到非边缘处.可见,RSF方法的稳定性和水平集的演化速度有待进一步提高.
2 本文算法
2.1 融合局部能量和梯度敏感性的水平集模型
图像梯度是描述图像特征的一个重要信息,在曲线演化过程中,具有重要的指导作用.为了提高水平集分割方法的稳定性以及水平集的演化速度,本文采用梯度信息构造梯度敏感项,并结合局部能量项,提出基于图像局部能量和梯度敏感性的水平集分割方法,定义水平集能量泛函如下:

式中:Φ(u,▽I)为梯度敏感的外部能量函数; G(u,▽I)为梯度敏感的内部能量函数;γ和ρ为Φ(u,▽I)和G(u,▽I)的权值,γ较大时,Φ(u,▽I)将零水平集拉向目标边界的作用增强;ρ较大时,G(u,▽I)将加快零水平集离开灰度均匀区域的速度.
采用梯度下降法最小化能量泛函E(u),得到水平集演化的速度函数
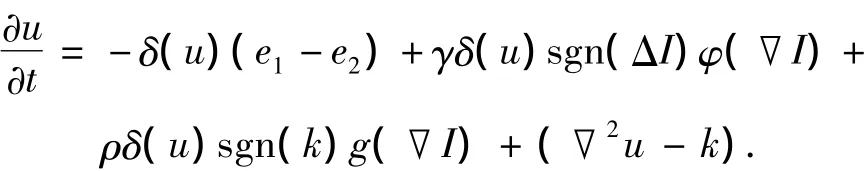
式中:ei由ξx(u,f1(x),f2(x))导出,

Heaviside函数及其导数分别定义为
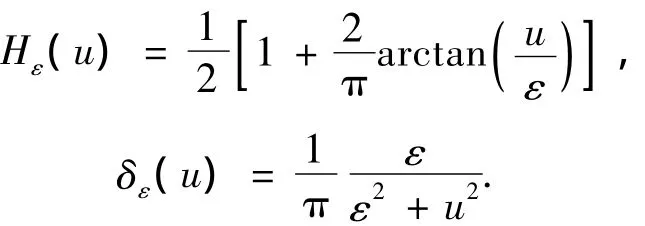
式中,参数ε控制了图像域内各点的驱动能量在速度函数中的权重,实验中选取ε=1.
基于图像局部能量和梯度敏感性的水平集模型中,水平集的运动受到2种外力的支配,1种是来自图像局部灰度能量的外力,1种是来自图像梯度特性的外力.在图像的不同区域,都有相应的力驱动水平集运动.下面对梯度敏感项做详细介绍.
2.2 梯度敏感的外部能量函数
为了矫正局部能量项导致的水平集演化错误,加快零水平集向目标边界的运动速度,提出如下的梯度敏感的外部能量函数:

式中:sgn(·)是符号函数,ΔI是由拉普拉斯算子定义的图像的二阶导数.|▽I|是图像梯度的模,φ(▽I)是归一化的梯度响应函数,b是梯度敏感因子.图像灰度值在[0,255]区间时,b取值为[5,15].
利用图像二阶导数在边界低灰度值的一侧为正,高灰度值一侧为负的过零点性质,定义能量函数Φ(u,▽I)的符号为sgn(ΔI).从而,梯度敏感的外部能量函数可以依据图像的梯度信息自适应地判定对水平集的驱动方向,避免了人工设定符号对初始位置的依赖,以及由此带来的应用局限性和边界泄露问题,如GAC模型中的面积项[5].
Φ(u,▽I)的强度由φ(▽I)确定,而敏感因子b决定了φ(▽I)对不同梯度值的响应度.图1给出了当max(|▽I|)=50时,不同b值对应的响应曲线.由图可知,φ(▽I)只对大于一定强度的梯度值有响应,对小于这个强度的梯度不响应或者响应度趋于零.随着b的增大,梯度响应阈值增高,响应范围缩小.调节φ(▽I)的响应特性,能够实现不同强弱程度边缘的提取.例如,降低b的取值,可以提取出图像中的弱边缘.
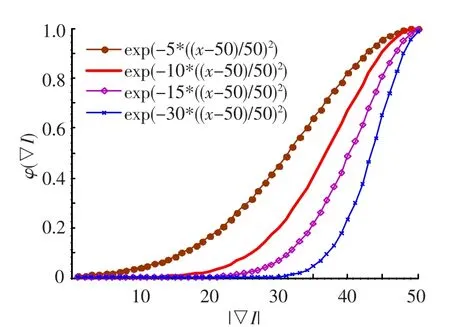
图1 不同b值时φ(▽I)的梯度响应曲线
可见,梯度敏感的外部能量函数的取值主要与图像的梯度信息相关,在灰度不均匀区域具有显著的驱动力.符号距离函数u对Φ(u,▽I)的影响远小于对ξx(u,f1(x),f2(x))的影响.因此,Φ(u,▽I)的引入能够提高水平集分割算法的稳定性,加速零水平集的收敛.
2.3 梯度敏感的内部能量函数
为了提高水平集在图像灰度均匀区域的演化速度,设计了梯度敏感的内部能量函数
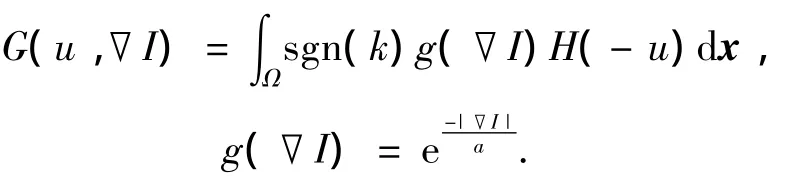
式中:k=div(▽u/|▽u|)是演化曲线的曲率; g(▽I)是归一化的梯度响应函数;a是梯度敏感因子,图像灰度值在[0,255]区间时,a取值为[1,10].
梯度敏感的内部能量函数G(u,▽I)对水平集的驱动方向由sgn(k)决定.曲率为正的水平集曲线向内部收缩,曲率为负的水平集曲线向外部扩张.系数a控制着g(▽I)收敛到零的速度,如图2所示.G(u,▽I)主要作用于灰度均匀区域,具有推动零水平集离开平坦区域的作用,与梯度敏感项的外部能量项互为补充.同时该项还能平滑轮廓曲线,约束新轮廓的产生.

图2 不同a值时g(▽I)的梯度响应曲线
2.4 水平集自动初始化方法
为进一步提高算法的效率,本文根据局部能量模型的特点,提出利用区域极值初始化灰度拟合函数,实现水平集自动初始化的方法.具体步骤为:首先对图像的灰度分布做直方图统计,并采用二次差分法绘出直方图的包络线.然后,对包络线上的点再次求取二次差分得到一组极大值点.将极值点排序后找出灰度值概率密度最大的3个点,用这3个点中灰度值最低的点初始化f1,灰度值最高的点初始化f2.最后,代入u=c0*sgn(-(e1-e2)),完成自动初始化.
图像的直方图表征了图像灰度的全局概率分布情况,因此包络线的极大值点所对应的灰度值代表着图像的主要灰度分布区域的灰度中心.本文对f1和f2的初始化是图像区域灰度中心估计与灰度拟合函数初始化的有机结合.可视为将局部域扩展到整幅图像的一种特例.自动初始化完毕后,零水平集基本位于目标边界附近,这不但免去了交互式的手动初始化,而且提高了算法的效率.
2.5 算法实现
采用中心差分法迭代求解速度函数,时间步长Δt=0.1.φ(▽I)和g(▽I)在迭代中可作为常量使用.求解速度函数前,需要先对灰度拟合函数f1和f2进行更新.算法的计算量主要在于每次迭代时求解-δ(u)(e1-e2)、f1和f2的4次卷积运算.本文算法的流程图如图3所示.
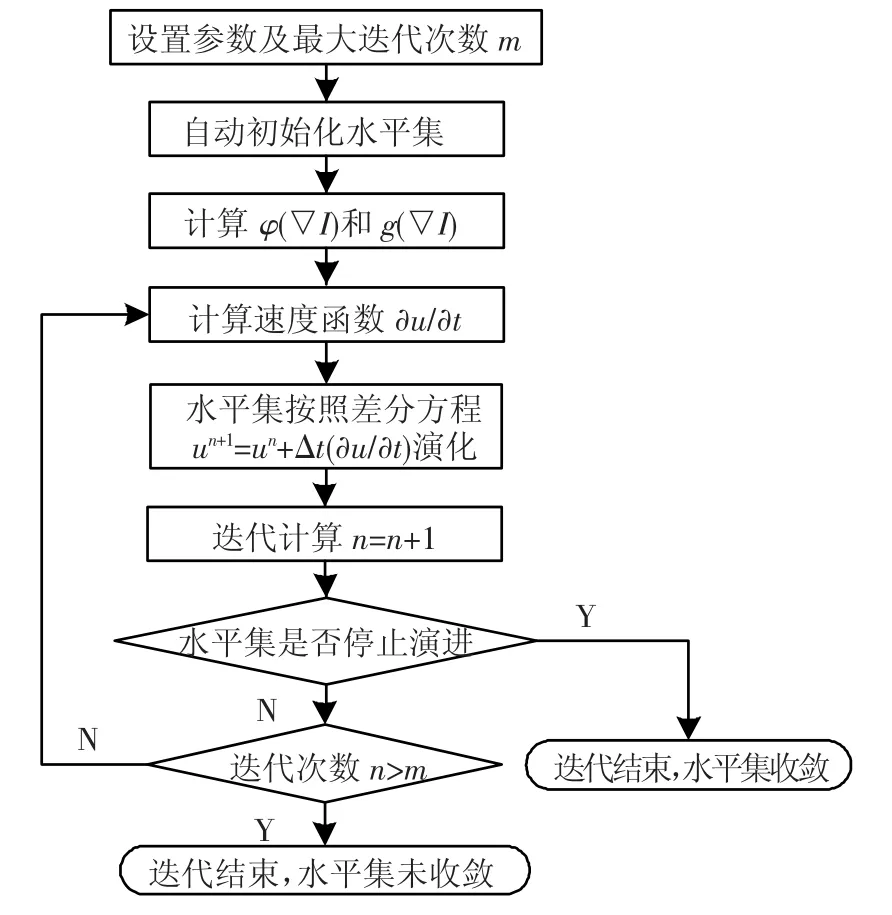
图3 算法流程
3 实验结果
为了验证算法的有效性,对本文算法和RSF算法进行实验对比.除特殊说明,设定实验参数为:σ=3,v=0.003×255×255,a=10,b=5,γ=0.03×255×255,ρ=0.006×255×255.
实验1 采用多目标的米粒图像验证算法的稳定性.手动初始水平集如图4(a),本文算法迭代70次后准确分割出每个米粒,结果如图4(b)所示.RSF算法在迭代290次后,水平集收敛如图4(c),无法分割出初始轮廓附近的米粒.改变水平集初始轮廓如图4(d)所示,本文算法和RSF算法的分割结果见图4(e)和4(f).可以看出,本文方法对水平集初始轮廓的敏感性降低,算法的稳定性得到提高.

图4 米粒图像分割结果对比
实验2 采用大脑MRI图像验证算法的准确性.大脑MRI图像结构复杂,含有内、外多层轮廓.采用图5(a)所示的自动初始化零水平集,本文算法和RSF算法的分割结果分别见图5(b)和图5(c).由图可知,本文算法和RSF算法都能分割出大脑的内外层轮廓,而本文算法对弱边缘和细节的提取更准确,具体可参见2个ROI区域的局部放大图5(d)~(g).实验选取a=2、b=5,此时梯度敏感的外部能量函数对弱边缘有响应,因此算法能够提取出弱边缘.可见,本文算法可以根据分割需要调节梯度敏感因子,实现对图像不同强弱边缘的提取.

图5 大脑MRI图像分割结果
实验3 对算法采用不同初始化方法所需的收敛时间与RSF算法进行了对比,并给出一个自动初始化实例.图6(a)为米粒图像的直方图,从图中包络线的极值点(由实心圆点标注)中选出3个极大值点,即为左起的第2、3、5点.其中,灰度值最低点为(19,616),最高点为(232,495).初始化f1=19,f2=232,相应的水平集自动初始化如图6(b)所示.自动初始化后,零水平集曲线基本位于目标边界的附近.在此初始化基础上,水平集能够快速收敛.

图6 米粒图像水平集的自动初始化
表1给出了针对4幅不同的图像,本文算法与RSF算法在分别采用水平集手动初始化和自动初始化的收敛时间.2种算法使用同样的初始轮廓,算法收敛所需的CPU时间和图像尺寸如表1所示.程序运行环境为Intel Pentium Dual E2140 1.60 GHz,内存2.00 GB,操作系统为Windows XP,应用Matlab2006a编程.由表可知,无论采用哪种初始化方法,本文算法的收敛时间都小于RSF算法的1/3倍.而采用自动初始化方法,算法的效率较手动初始化也得到显著的提高.

表1 本文算法与RSF算法的收敛时间对比 s
4 结论
1)本文融合了图像的局部灰度信息和梯度信息,提出了一种基于图像局部能量和梯度敏感性的自动初始化水平集分割算法,可以实现灰度不均匀图像、多目标图像、结构复杂的多层轮廓图像的分割.
2)局部能量项强调图像的局部信息,是对传统C-V模型全局优化思想的改进.梯度敏感的外部能量函数的提出有助于提高水平集演化的稳定性.
3)通过调节梯度敏感因子,可以控制算法对不同强弱边缘的响应度,准确提取出弱边缘.通过初始化灰度拟合值,实现了水平集的自动初始化,进一步提高了算法的效率.
4)与RSF算法相比,本文算法稳定性好、收敛速度快,分割结果更准确,且不需要交互操作.
5)理论上,本文算法可以推广到多相水平集,相应的多相水平集模型及自动初始化方法有待进一步的研究.
[1]CHENOUNE Y,DELECHELLE E,PETIT E,et al. Segmentation of cardiac cine-MR images and myocardial deformation assessment using level set methods[J]. Computerized Medical Imaging and Graphics,2005,29 (8):607-616.
[2]DRAPACA CS,CARDENAS V,STUDHOLME C.Segmentation of tissue boundary evolution from brain MR image sequences using multi-phase level sets[J]. Computer Vision and Image Understanding,2005,100 (3):312-329.
[3]XU C,PRINCE J L.Snakes,shapes,and gradient vector flow[J].IEEE Trans on Image Processing,1998,7(3):359-369.
[4]CASELLES V,CATTE F,COLL T,et al.A geometric model for active contours in image processing[J].Numerische Mathematik,1993,66(1):1-31.
[5]CASELLES V,KIMMEL R,SAPIRO G.Geodesic active contours[J].International Journal of Computer Vision,1997,22(1):61-79.
[6]何传江,李梦,詹毅.用于图像分割的自适应距离保持水平集演化[J].软件学报,2008,19(12): 3161-3169.
[7]CHAN T,VESE L.Active contours without edges[J]. IEEE Trans on Image Processing,2001,10(2):266-277.
[8]原达,张彩明,李晋江,等.基于Mumford-Shah模型的高精度MR图像轮廓提取算法[J].计算机学报,2009,32(2):268-274.
[9]VESE L,CHAN T.A multiphase level set framework for image segmentation using the Mumford and Shah model[J].International Journal of Computer Vision,2002,50(3):271-293.
[10]CHEN S,SOCHEN N A,ZEEVI Y.Integrated active contours for texture segmentation[J].IEEE Trans on Image Processing,2006,15(6):1633-1646.
[11]LI C,KAO C,GORE J,et al.Minimization of regionscalable fitting energy for image segmentation[J]. IEEE Trans on Image Processing,2008,17(10): 1940-1949.
