基于非支配排序遗传算法的效果评价及程序测试*

韩荣荣 陈 益 周建淞 张晓丽 李飞莹 师先锋 仇丽霞△

医学实践中经常遇到多目标优化问题，由于实际问题常由多个相互冲突的指标组成，问题的解通常不是单个的最优解，而是一组非劣解，因而采用传统多目标优化方法通常无法解决〔1〕。遗传算法是模拟生物自然进化的一种有效优化搜索方法，在数值优化、组合优化、人工生命等方面解决了传统方法遇到的技术难题。它可对代表整个解集的种群不断进化，以内在并行方式搜索多个非劣解(Pareto解集)，非常适合多目标优化。本文旨在应用四个标准测试函数对英国Glasgow大学软件工程师陈益提供的外挂工具箱(SGALAB)beta5008中NSGA程序进行可靠性测试，为NSGA的实际应用提供理论依据及可行的程序。

NSGA方法原理

非支配排序遗传算法〔2〕(nondominated sorting genetic algorithm，NSGA)是由 Srinivas和Deb于1995年提出的，是一种基于Pareto排序的方法，其基本思路是对所有的个体按不同的层次分级，在执行选择算子之前，种群已经根据支配与非支配关系进行了分级排序，并且种群中的所有个体都被指定一个虚拟适应度值(一般情况下和种群规模成一定比例)，同级个体的虚拟适应度值相同，这样就保证了同级个体有同样的复制概率。为了维持种群多样性，这些分级后的个体共享它们的虚拟适应度值。NSGA的特点在于将多个目标函数计算转化为虚拟适应度计算。NSGA可以处理多个目标函数的优化问题，并且可以处理最大化或最小化问题。算法流程如图1所示。

测试方法与步骤

1．测试函数及其特点

(1)两目标简单测试函数、两目标复杂测试函数(A)与三目标测试函数及其特点见文献〔3〕。

(2)两目标复杂测试函数(B)〔4〕及其特点

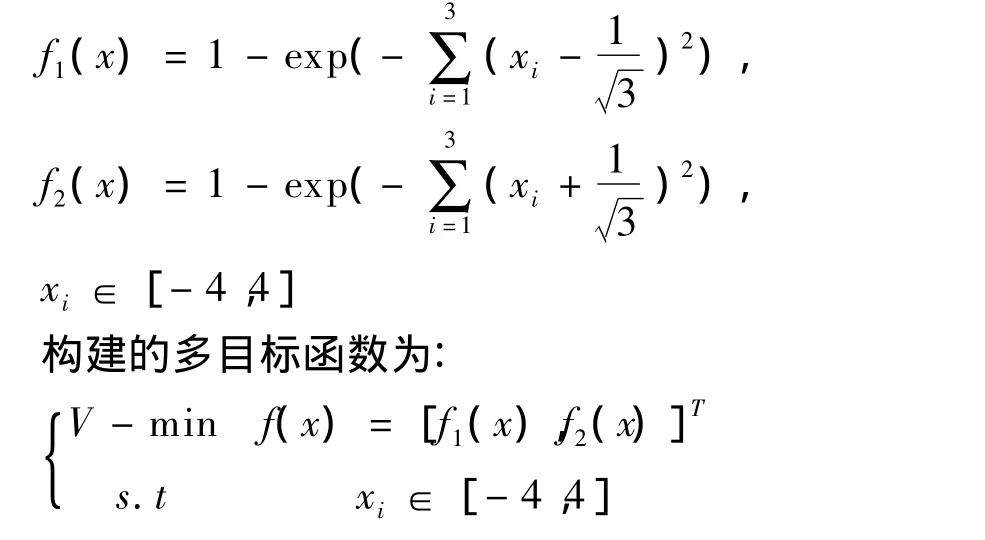
2．遗传算法参数设置

采用二进制编码，取初始种群(population)=30，进化代数(generation)=100，单点交叉概率(probability-crossover)=0.90，变异概率(probability-mutation)=0.01，简单函数两目标和复杂函数单目标优化均运行20次，复杂函数两目标优化运行100次。

3．遗传算法性能评价

(1)在线性能评价 采用平均适用度进化曲线评价算法的动态性能。

(2)离线性能评价 最大适用度进化曲线反映解的变化，评价算法的收敛性。

4．软件及统计分析

选用数学功能较强的美国矩阵实验Matlab2009a软件绘制函数图形;利用英国Glasgow大学软件工程师陈益提供的Matlab2009a外挂SGALAB工具箱beta5008完成遗传算法寻优;利用SPSS13．0软件进行统计分析。

NSGA求解测试结果

1．两目标简单测试函数的Pareto非劣解集

非支配排序遗传算法(NSGA)给出的两目标简单函数的20个Pareto非劣解方案见表1，从其中一个方案的世代进化曲线图2、图3可以看到，两个目标函数的最大、平均适应度曲线大约在进化3代以后就稳定在1的附近，反映了NSGA具有较好的收敛性，动态性能好;图4为NSGA搜索的Pareto非劣解前端，非劣解沿一条曲线分布，表面大多数非劣解都可以搜索到。由表2可知，20次随机搜索结果的平均水平为1.01，标准差为0.16，95%可信区间包含交叉点1。f1(x)的平均水平为1.04，标准差为0.34，f2(x)的平均水平为1.01，标准差为0.30。符合两目标简单测试函数的特点。即NSGA能够给出合理的Pareto解集。

表1 NSGA求解两目标简单函数的Pareto非劣解

2．两目标复杂测试函数(A)的Pareto非劣解集

利用NSGA搜索使复杂测试函数 f1(x1，x2)、f2(x1，x2)同时最小，100个Pareto非劣解方案见表3，研究者可以根据实际工作的需要选择合适的解;从其中一个方案的世代进化曲线(图5、图6)可知，两个目标函数中的f1(x1，x2)的最大适应度曲线大约在进化1代以后就稳定在函数值为0.2的水平附近，平均适应度曲线大约在进化3代以后就稳定在函数值为0.2的水平附近，而f2(x1，x2)的最大适应度曲线大约在进化5代以后就稳定在函数值为15的水平附近，平均适应度曲线大约在进化5代以后就稳定在函数值为15的水平附近，图5反映出算法具有较好的收敛性，图6反映了算法的动态性好;图7为NSGA非劣解前端分布，其解前端呈带状分布，显示了两目标互为冲突的特点，很好地反映了两目标间的关系。表4给出NSGA随机搜索100次结果的平均水平:在x1=0.89，x2=0.50 时，f1(x1，x2)、f2(x1，x2)均达到最小，分别为0.89，1.75。¯x±s

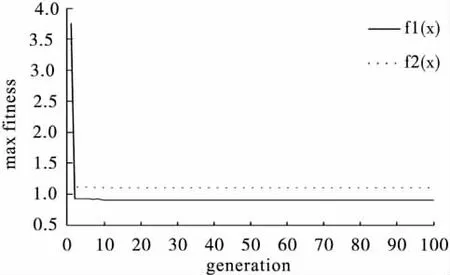
图2 两目标简单函数NSGA max fitness—generation

图3 两目标简单函数NSGA mean fitness—generation

95%

分布范围

Lower upper

最小值 最大值

x 1．01 ±0．16 0．93 1．08 0．80 1．41

f1(x) 1．04 ±0．34 0．88 1．20 0．64 1．99

f2(x) 1．01 ±0．30 0．87 1．15 0．35 1．44

图4 两目标简单函数NSGA Pareto非劣解前端分布

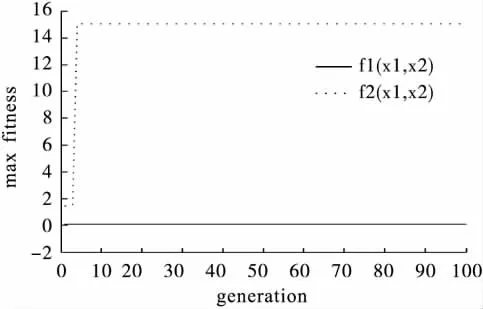
图5 NSGA max fitness-generation

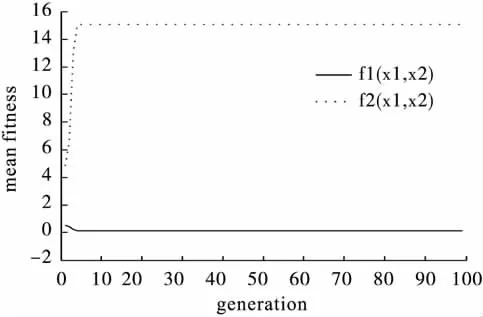
图6 NSGA mean fitness-generation

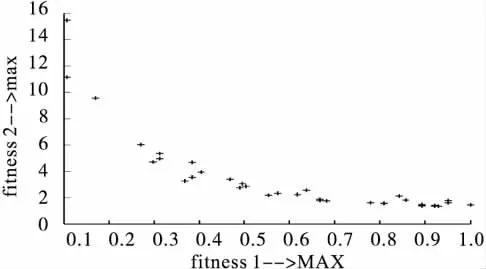
图7 两目标复杂函数NSGA Pareto非劣解前端分布

表3 NSGA求解两目标复杂函数(A)的Pareto非劣解

表4 两目标复杂函数值(A)及Pareto非劣解平均水平

3．三目标复杂测试函数的Pareto非劣解集

NSGA搜索使三目标测试函数f1(x1，x2)，f2(x1，x2)，f3(x1，x2)同时最小，100个 Pareto非劣解方案见表5，研究者可以根据实际工作的需要选择合适的解;从其中一个方案的世代进化曲线(图8、图9)可知，三目标函数中的f1(x1，x2)的最大适应度曲线大约在进化5代以后就稳定在函数值为2的水平附近，平均适应度曲线大约在进化4代以后就稳定在函数值为2的水平附近;f2(x1，x2)的最大适应度曲线大约在进化1代以后就稳定在函数值为15的水平附近，平均适应度曲线大约在进化3代以后就稳定在函数值为15的水平附近;而f3(x1，x2)的最大适应度曲线大约在进化2代以后就稳定在函数值为0的水平附近，平均适应度曲线大约在进化1代以后就稳定在函数值为0的水平附近，图8的最大适应度曲线反映出算法具有较好的收敛性，图9的平均适应度曲线反映了算法的动态性好;图10为NSGA非劣解前端分布，其解前端是一个非线性的，非对称的三维曲面，符合三目标理论解集的分布情况。表6是NSGA对三目标函数100次随机搜索结果的平均水平:x1=0.44，x2=－0.03时，三目标函数值 f1(x1，x2)、f2(x1，x2)、f3(x1，x2)均达到了最小值，平均水平分别为 1.74，20.10，0.19。

表5 NSGA求解三目标函数的Pareto非劣解

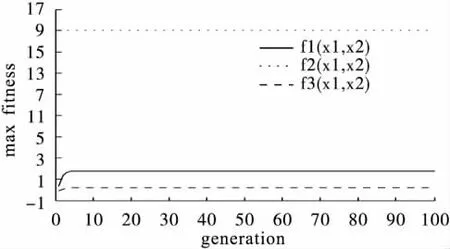
图8 NSGA max fitness-generation

图9 NSGA mean fitness-generation

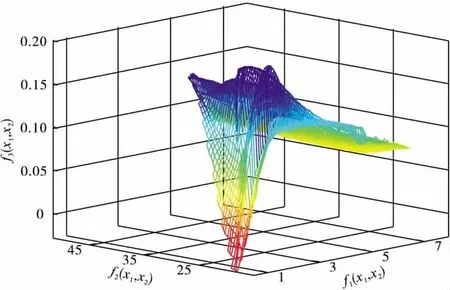
图10 三目标复杂函数NSGA Pareto非劣解前端分布

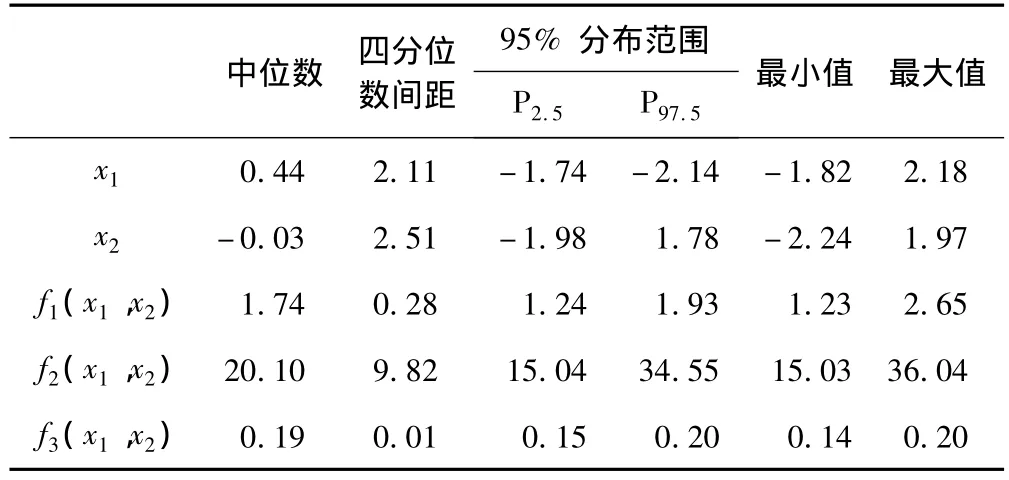
表6 三目标函数值及Pareto非劣解平均水平

4．两目标复杂测试函数(B)的Pareto非劣解集

利用 N SGA 使测试函数 f1(x1，x2，x3)、f2(x1，x2，x3)同时最小的前30个Pareto非劣解方案见表7，第

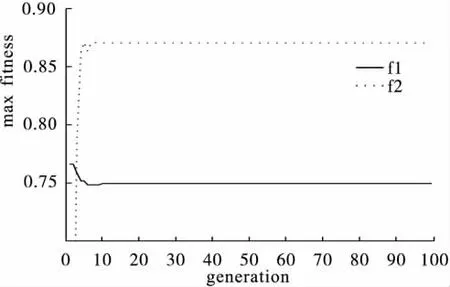
图11 NSGA max fitness-generation

图12 NSGA mean fitness-generation

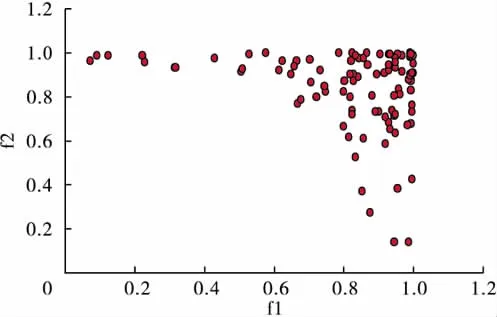
图13 两目标复杂函数(B)NSGA Pareto非劣解前端分布

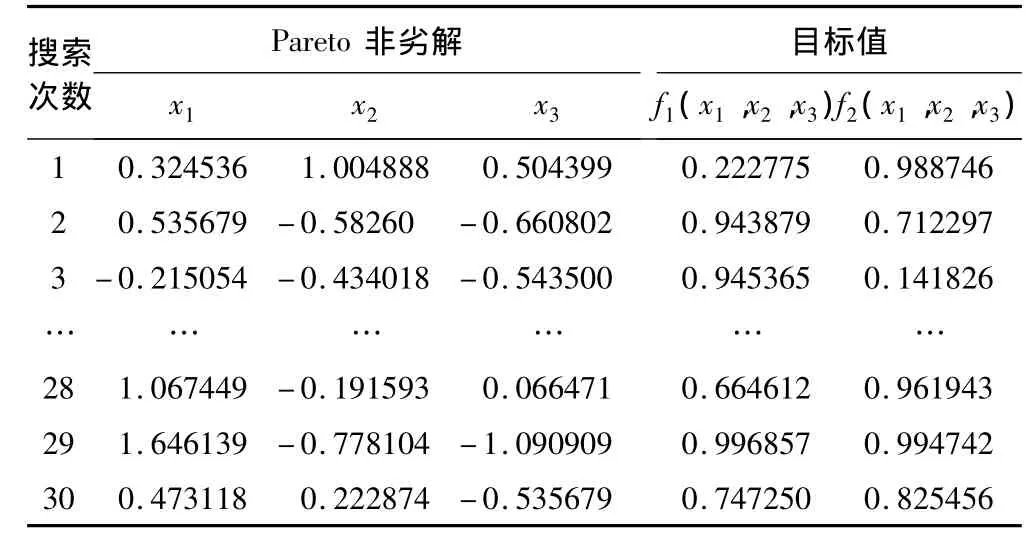
表7 NSGA求解复杂函数(B)的Pareto非劣解

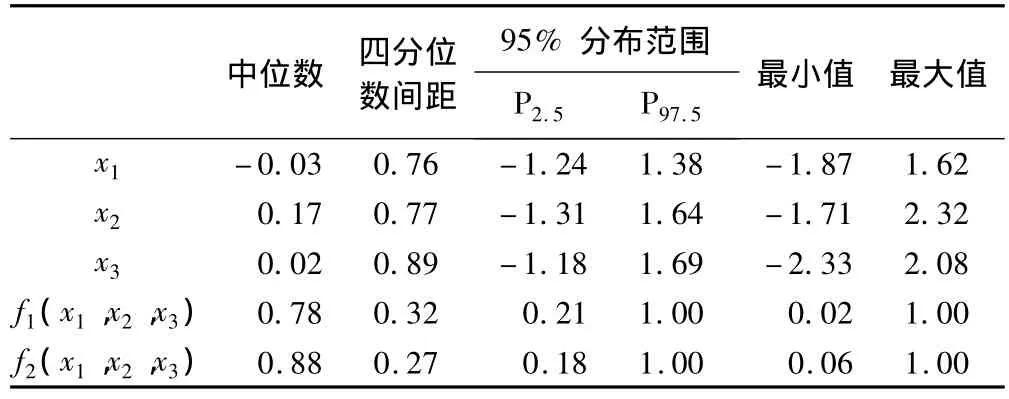
表8 两目标复杂函数(B)的值及Pareto非劣解平均水平

讨 论

本文利用Matlab2009a外挂SGALAB工具箱beta5008，分别对简单测试函数、两个复杂测试函数与三目标测试函数进行多目标寻优。结果表明NSGA进行多目标优化效果理想，程序可行，搜索到的Pareto非劣解合理，为实际应用提供了合理的选择空间。NSGA为多目标寻优问题提供了可行的方法，可与均匀试验设计相结合，寻求最优试验条件，达到节省人力、物力、提高有效成分提取效率、降低研究成本的目的。

1．谢涛，陈火旺，康立山．多目标优化的演化算法．计算机学报，2003，8(26):997-1003．

2.Srinivas N，Deb K．Multi-Objective function optimization using nondominated sorting genetic algorithms．Evolutionary Computation，1995，2:221-248．

3.李飞莹，陈益，师先锋，等．基于小生境遗传算法的多目标药物提取条件优化分析应用．中国卫生统计，2010，27(6):577-581．

4.Deb K，Pratap A，Agarwal S，et al．A fast and elitist multi-objective Genetic Algorithm:NSGA-Ⅱ．Kanpur Genetic Algorithms Laboratory(Kan-GAL)．