煤矿动态轨道衡数据采集与处理

陈 建，郑传行，陈建中

（贵州财经学院信息学院，贵州贵阳 550004）

煤矿动态轨道衡数据采集与处理

陈 建，郑传行，陈建中

（贵州财经学院信息学院，贵州贵阳 550004）

研究了煤矿动态轨道衡中称重传感器安装、数据采集以及信号处理方法，目的是实现矿山恶劣环境下的高精度煤矿动态称重。提出轮计重的称重方式，并对称重传感器采取交错式安装以实现准确的方向判别，采集并提取出有效称重信号后，结合经验模态分解方法进行重量的计算。实验结果表明，该方法实现了“准”、“快”、“省”的称重目标。

动态轨道衡;数据采集;称重传感器;经验模态分解

由于恶劣的矿山检测环境导致系统测量精度低、可靠性差，煤矿动态轨道衡一直没有成熟产品。目前铁路轨道衡或公路动态衡多采用轴计重方式［1－2］，即过车时对前后轴分别采集数据并计算重量。这种方式对运行环境、硬件设备等要求很高，在基础条件好、车辆运行稳定条件下能得到较好的测量效果。但是，矿山环境中由于存在矿车冲击大、轨道不平、轮轴变形、运行不稳以及硬件资源有限等各种不利因素，采用轴计重方式易导致车辆误判等问题，无法达到准确的基本计量要求。

矿车非停车状态下的动态衡称重，与停车状态下的静态衡称重相比，必须体现快速的优点，这是因为动态衡的称重设备一般安装在井口附近，如果称重过程缓慢会导致矿车在井口积压，甚至引起矿车向矿井中回灌倒车，将会带来严重安全隐患。

要在恶劣矿山环境下利用有限系统资源 （存储容量、计算速度、传输速度等）实现既准又快的测量目标，则系统资源节省问题的考虑至关重要。大量实验表明，现有的各种铁路轨道衡或公路动态衡称重方法［3－5］，不仅对运行环境要求高，而且算法复杂、系统资源损耗大，在煤矿动态轨道衡中应用时效果不佳。

综上所述，“准”（计量准确）、“快”（速度快）、“省”（系统资源节省）是煤矿动态轨道衡计量的三大要求，是实现高精度称重的重点与难点。

1 数据采集与预处理

在煤矿动态轨道衡中，称重传感器将重量外力变换为电信号后，数据采集器对信号进行采集、滤波、零点校正、上下衡判别并截取有效称重信号，该过程称为系统的数据采集与预处理。

1.1 称重传感器的交错式安装实现准确判车

分别对矿车每一个轮的运行采集数据并计算重量，各轮重量相加得到整车重量，称为轮计重方式。该方式具有采集样本数据多、判车准确等优点，同时能够有效处理矿车偏载、轮轴变形、运行不稳等各种不利因素带来的影响，在矿山环境下将比轴计重方式获得更高的称重精度。

煤矿动态轨道衡应用中要求对出井方向矿车称重，而对入井方向的矿车不称重或进行除皮操作，故矿车运行方向的准确判断是实现精确称重的前提。现有的煤矿动态衡多采用红外对射探测器或独立的方向传感器对运行方向进行判断，需安装的设备繁杂、施工难度大，且在矿山环境下使用容易出错。此外，由于本方法采取轮计重方式，对于矿车振动等原因引起的车轮反复现象，现有的设备很难准确识别，常会导致重复称重。因此，提出称重传感器的交错式安装方法，系统不需要安装红外对射探测器或独立的方向传感器就能对矿车方向作出正确判别，对于反复倒车亦能准确判断。具体安装见图1，在平行的两条轻轨之间分别安装称重传感器1与2，并将2个传感器沿矿车运动方向一前一后错开一定位置L，下面将通过图2示意进行论证:L的正确选取是实现准确判车的关键。论述中，将车轮踏上传感器的动作称为上衡，离开传感器的动作称为下衡。

图1 称重传感器的交错式安装

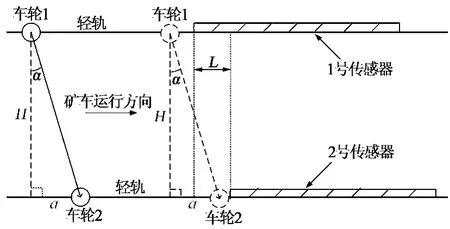
图2 轴变形矿车的方向判别

首先，L长度不能太小。若矿车无轴变形，即图2中矿车轴变形的偏移角α=0，则矿车从左向右运行时，同一轴上的轮1将比轮2先上衡，系统根据两轮上衡先后作出方向的正确判断。然而，实际矿车常存在严重的轴变形，即矿车轴变形的偏移角α≠0。设两轻轨之间的轨距为H，则同一轴上两轮由于轴变形在运行方向上产生了距离差a= Htanα，当矿车运行至传感器处，若两传感器错位长度L＜a=Htanα，则轮2会先上衡，系统将根据两轮上衡先后判断矿车从右向左运行，从而导致了误判，因此，L需满足:L＞a=Htanα。

其次，L长度也不能太大。由于系统采集的有效称重数据来源于同轴两轮在传感器上同时在衡时的数据，故必须保证同轴两轮在传感器上有足够的同时在衡时间，即保证两传感器的重叠区域足够长，理论与实验证明两传感器的重叠长度不能小于250mm（由于篇幅问题证明略），而如果L过大将导致两传感器的重叠长度太短。

根据前述理论分析结合实践经验，实际安装中L可按公式（1）进行计算:

式中，H为两轻轨之间的轨距;α为矿车轴变形的最大偏移角;e为安全系数 （1＜e＜2）。

1.2 上衡前的数据滤波与零点校正

启动系统并对称重传感器输出的信号进行采集，在车轮上衡之前传感器承重为零，此时的采集称为零点采集。如果矿车出车时间间隔长，则零点采集在一定时间后将积存大量零重数据，给系统的存储与传输带来困难。另外，系统采集到的尖脉冲噪声常会导致车轮上衡的误判。因此，在零点采集过程中对信号进行32点均值滤波，这样既能抑制尖脉冲噪声带来的上衡误判，也能大大减少数据的存储与传输量，具体方法为:每连续采集的34个点，剔除最大最小值点后，把剩余32个点的平均值作为信号有效点进行存储。

系统的零点采集过程，是矿车到来前的系统等待过程，同时也是称重零点的校正过程。设定零点校正间隔时间T，若系统持续零点采集时间达T后仍未有车轮上衡，则将时间T内的零点采集数据的平均值作为系统新的称重零点，并清除在此之前的零点采集数据。

1.3 上下衡之间的数据记录

估算矿车重量并设置上下衡判别阈值h，系统随时将零点采集的信号有效点与h相比较，若信号大于h，则判断车轮己上衡，系统停止零点采集并开始记录称重数据，同时将32点均值滤波改为4点均值滤波，这样既能抑制尖脉冲噪声可能造成的车轮下衡误判，也能获取尽量多的数据点用于称重。连续记录到所采集的信号小于h时，系统判断车轮已下衡并停止记录重量数据。图3所示为系统按本步骤记录到的某车轮上下衡之间信号。

图3 车轮上下衡间数据信号

1.4 车轮有效称重信号的截取

由于系统的2个称重传感器采取了交错式安装，对于两传感器安装的非重叠区域，矿车通过时同一轴上的两轮将不能同时在衡，对于该区域内的采集数据不能用于称重，必须进行截除处理。另外，安装基础不稳、矿车的轮轴变形等因素，都会在车轮上下衡时造成严重信号冲击，在图3上体现为两端可能出现的尖峰振荡，该振荡不属于重量的稳态信号，故不能用于重量计算，需要截除。

综合上述对于传感器错位以及信号冲击的考虑，并按照“快”且“省”的算法设计原则，系统在实际处理中对步骤1.3截取出的上下衡间信号两端各截除1/4后，得到最终有效轮称重信号，由图3信号得到的最终有效轮称重信号见图4。

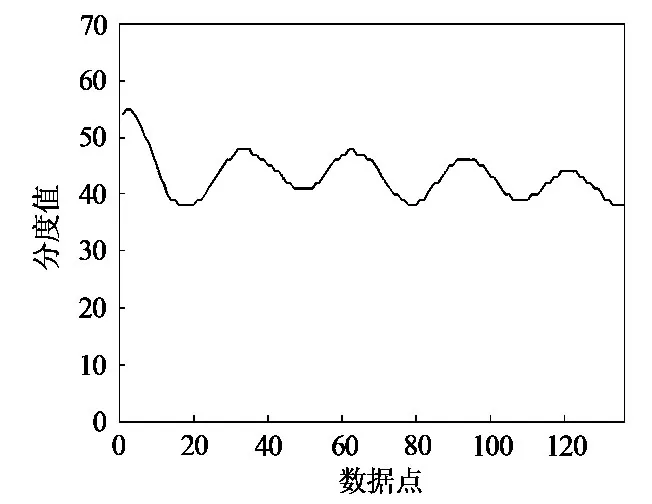
图4 车轮有效称重信号

2 基于经验模态分解的称重信号处理

2.1 经验模态分解

经验模态分解 （Empirical Mode Decomposition，EMD）是美国国家航空航天局 （NASA）的Huang N E等［6］在1998年首先提出的一种新的信号处理方法，是目前提取短数据序列趋势和均值的最好方法。EMD方法认为，任何信号都可分解为若干阶本征模函数 （Intrinsic Mode Function，IMF）与一个残余量，其中IMF要满足2个条件:整个数据集的极大值、极小值的数目和穿越零点的次数要相等或最多相差1;极大值点确定的上包络线和极小值确定的下包络线的均值要始终为零。EMD分解的具体步骤如下:

（1）对于分解的信号y（t），找出y（t）上所有的极值点，用3次样条曲线连接所有的极大值点，形成y（t）的上包络线;连接所有极小值点，形成y（t）下包络线。定义上下包络线的均值为m（t），y（t）与m（t）的差值设为（t）=y（t）－m（t）。

（2）如果（t）不满足IMF的2个条件，则令y（t）=（t），然后重复步骤 （1），得到（t）;经过k次迭代，直至得到（t）满足IMF的2个条件，定义信号y（t）的第一阶IMF分量C1（t）=（t）。

（3）设r1（t）=y（t）－C1（t），令新信号y（t）=r1（t），重复步骤（1）、（2），得到二阶IMF分量C2（t）;再令r2（t）=y（t）－C2（t）作为新的信号y（t），按此方法继续分解，直至标准方差SD的大小在0.2～0.3或残余量已经成为单调函数，其中:

这样原始信号y（t）可以表示成各阶IMF与一个残余量rn（t）的和:

2.2 基于EMD的称重算法

在系统的计量控制器中，将图4的有效称重信号进行EMD分解后见图5，分解得到各阶IMF分量 （C1，C2，C3）和残余量r，各阶IMF分量反映的是污染轮重信号的各种额外动态载荷，而r反映了真实轮重。

因此，把r作为实际重量信号并求取平均值即可得到对应车轮的重量分度值。

图5 有效称重信号的EMD分解

影响系统测量精度的因素主要有:环境干扰、轮轴变形、基础不稳、矿车速度以及系统误差等。当系统安装运行后，如果环境与系统保持相对稳定，则一定时间内各种因素对精度的综合影响可以近似认为稳定，因此，可以将各种因素的影响综合考虑并用一个总的误差校正参数k进行补偿，将矿车重量分度值乘以k后得到校正后的真实重量。k的最佳取值很难通过理论推导得到，可通过实验获取:系统安装后，用标准重量的矿车进行实验，对k值以预设值为基准进行微调，选取测量精度相对最高时对应的k值。由于环境的稳定是相对的，因此，需要定期对系统k值进行实验校正。

通过上述方法可分别算出矿车每个轮上的重量，将4个轮上重量相加即得整车重量。

3 称重方法的实验验证

在实验室环境中，向实验矿车里添加标准称重砝码，并让矿车通过称重传感器进行测试。实验矿车净重的静态值为116.5kg，标准砝码的静态值为30.7kg/个，矿车速度1m/s。设每次实验中加砝码后矿车总重量的静态值为Ti，对应的动态测量值为Ci，定义该次动态测量的相对精度A为:

选取上下衡判别阈值h为25，首先对加5个砝码的矿车进行10次实验，对k值以预设值1.3为中心进行大小微调，每次微调0.01，选取10次实验测量精度平均值最高时的k=1.28为系统k值，然后再分别对加6～10个砝码的矿车进行10次实验，表1列出了10次实验的各项计算平均值。结果表明，采用上述矿车动态称重方法，测量结果与静态重量相比误差微小，相对测量精度很高。

表1 10次实验的平均计算结果

4 结束语

“准”、“快”、“省”是煤矿动态轨道衡计量最重要的要求，这3个指标的考虑贯穿了本方法始终，具体描述如下:

（1）交错式传感器安装设计巧妙，“省”了方向传感器等设备，并用最简单的方法解决了判车不“准”的问题。

（2）在采集过程中采取均值滤波并定时清零;不再进行其他复杂信号滤波或端点延拓处理;对上下衡的判别采用统一阈值;直接采用EMD分解的残余量作为实际重量信号，而忽略各阶IMF对重量计算的微弱影响。这些措施在保证“准”的前提下实现了“快”与“省”的目标。

（3）综合考虑多种因素对测量精度的影响，得到一个总的误差校正参数k，该方法与分别考虑各种因素的影响并一一进行校正的方法相比，既“快”又“准”。

［1］姚恩涛，季 娟，张 明.两轴车辆动态称重信号分析方法研究［J］.传感器技术，2005，24（12）:22－25.

［2］周志锋，蔡 萍，许 嘉，等.基于经验模态分解的汽车动态称重数据处理［J］.中国机械工程，2005，16（20）.

［3］许光悦.微机控制动态轨道衡的模拟量判别车型法［J］.传感器应用技术，1989，7（1）:11－16.

［4］郭兰英，梁 波，董安国.汽车动态称重的新方法［J］.长安大学学报 （自然科学版），2009，29（2）:98－100.

［5］盖广洪，吕小俊，张 伟.车辆动态轴重衡称重信号的自适应滤波方法［P］.中国发明专利:CN 10 l1054llA，2008.1.

［6］Huang N E，Shen Z，Long SR，et a1.The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non－stationary Time Series Analysis［J］.Proceedings of Royal Society A，1998，454（4）:903－995.

Data Collection and Analysis of Dynam ic RailWeighbridge for Coal Mine

CHEN Jian，ZHENG Chuan-xing，CHEN Jian-zhong

（Information School，Guizhou Finance＆Economics Institute，Guiyang 550004，China）

In order to realize high-precision dynamic weighing in underground wicked environment，this paper researched installation ofweight sensor，data collection and single dealtmethod in dynamic railweighbridge for coalmine.Turn weighing was put forward and interlaced installation was applied to realizing accuracy direction judgment.After collecting effective weighing single，weightwas calculated based on experiencemode decomposition method.Test result showed that thismethod was accuracy，fast and economical.

dynamic railweighbridge;data collection;weight sensor;experiencemode decomposition

TD274.2

A

1006-6225（2011）04-0089-04

2010－12－01

贵州省科技厅工业公关项目 （黔科合GY字［2010］3078）;贵州省重点技术创新项目 （黔经信办［2010］713）

陈 建 （1959－），男，贵州贵阳人，硕士，研究员，从事计算机应用技术研究。

［责任编辑:张银亮］