独塔悬索桥基本参数研究＊

蒋 望，邵旭东，彭旺虎，余加勇

（湖南大学土木工程学院，湖南长沙 410082）

独塔悬索桥基本参数研究＊

蒋 望，邵旭东†，彭旺虎，余加勇

（湖南大学土木工程学院，湖南长沙 410082）

基于挠度理论以及等代梁法，分析矢跨比和高跨比对主缆和索塔用量的经济性影响和结构受力变形的影响，得出矢跨比和高跨比在经济性和结构刚度方面的各自适用范围.为验证建议范围内的矢跨比和高跨比可以满足结构经济性的同时亦满足结构的受力变形要求，试设计一座独塔双主跨悬索桥，并与中国某三塔悬索桥进行比较分析.结果表明：独塔悬索桥主缆用量比三塔悬索桥减少约14%，索塔造价减少约3.5%.活载作用下独塔悬索桥主梁最大挠跨比、主梁最大转角以及塔顶最大纵向位移均小于三塔悬索桥.选择合适的矢跨比和高跨比的独塔悬索桥，可以兼顾结构的经济性和使用性，还可与三塔悬索桥方案竞争.

桥梁工程；独塔悬索桥；挠度理论；等代梁法；矢跨比；高跨比；三塔悬索桥

悬索桥是跨越能力最强的桥型，双塔悬索桥是被人们熟知并被广泛应用于跨越大江、大河的桥型.但是，当出现一些特殊情况（W型河床地形、河中为沙洲）时，采用独塔悬索桥［1－3］或三塔悬索桥［4－5］无疑是较为合适的.关于独塔悬索桥方面研究的论文较少，本文对这种桥型的基本性能做了若干探索性的研究，主要包括主缆和索塔经济性及结构受力变形研究，通过试设计一座独塔悬索桥，从结构受力的合理性和材料的经济性方面进行研究，并与中国某三塔悬索桥进行比较分析，初步提出有关独塔悬索桥设计中可供参考的技术参数.

1 合理矢跨比、高跨比结构变形影响

设计独塔悬索桥时（见图1），矢跨比、高跨比是重要的设计参数，本节以经济性为基础进行相关研究.

图1 独塔悬索桥简图Fig.1 Single-tower suspension bridge

1.1 等代梁法分析主梁结构受力变形

本节用等代梁法［6］分析悬索桥主梁挠度与主缆水平力之间的关系.

1.1.1 全跨均布荷载挠度分析

主梁在全跨为均布荷载q1作用下（见图2），任意点挠度λx为：

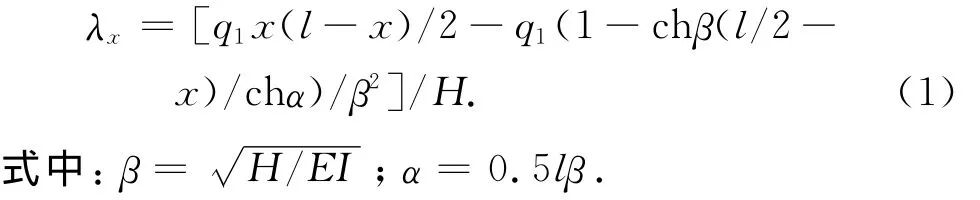
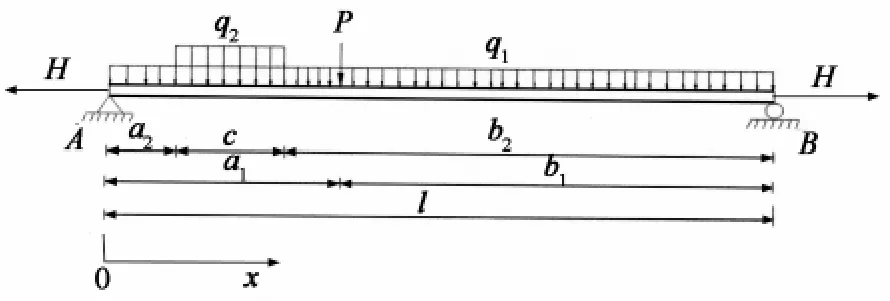
图2 荷载形式分布图Fig.2 Load distributions

1.1.2 任意长度均布荷载挠度分析

在任意长度c的均布荷载q2作用下，主梁任意点挠度λx为：

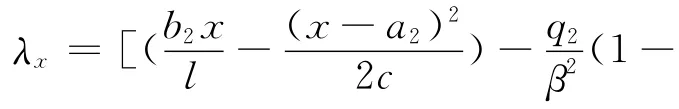
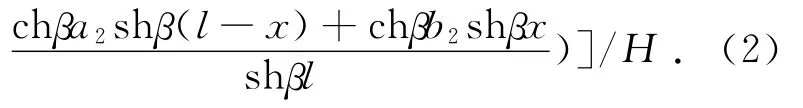
1.1.3 集中荷载挠度分析

在集中力荷载P作用下，主梁任意点挠度λx为：

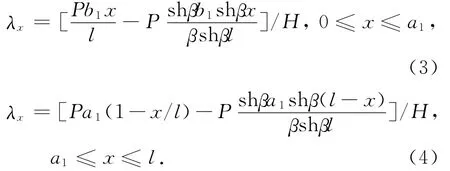
由式（1）～式（4），绘出主梁跨中挠度与主缆水平力关系图如图3所示（q1＝10.5 k N／m；q2＝93 k N／m；c＝60 m；P＝1 350 k N；l＝1 080 m；a1＝540 m；b1＝540 m；a2＝540 m；b2＝510 m）.由图3可知，集中力对挠度影响较小，均布荷载对结构挠度影响较大；主缆水平力决定了主缆的刚度，主缆水平力越大，主缆刚度越大，则主梁挠度越小.

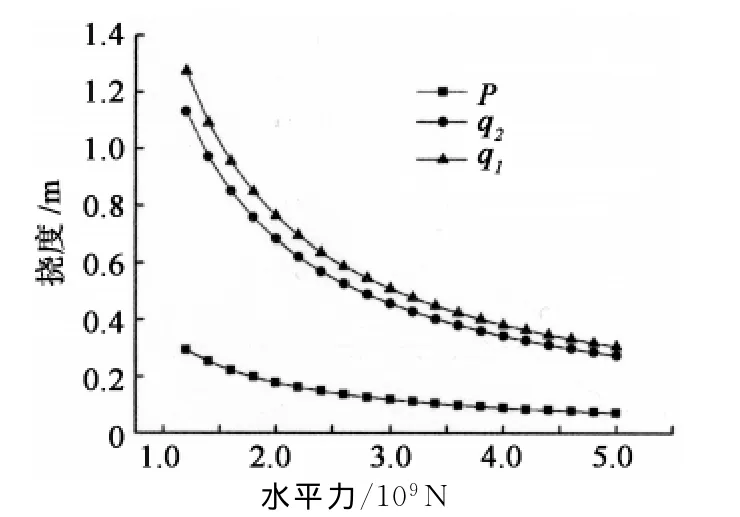
图3 主梁挠度与主缆水平力关系图Fig.3 Relation between deflection of main girder and horizontal force of main cable

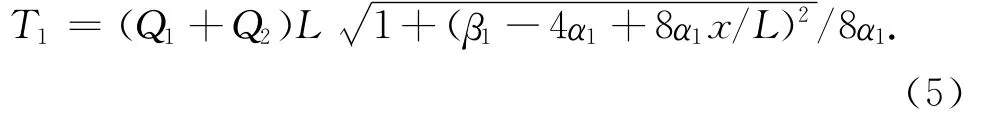
下面分别研究矢跨比和高跨比与主缆轴力的关系.在一期恒载Q1＝178.1 k N／m，二期恒载Q1＝53.1 k N／m作用下，主跨径600～1 000 m独塔悬索桥主缆轴力与矢跨比和高跨比关系曲线如图4和图5所示.

1.2.1 矢跨比α1与主缆轴力T1的关系

由图4可知，矢跨比α1越大，主缆轴力T1均越小；当α1＝0～0.12时，主缆轴力下降明显；当α1＝0.12～0.2时，主缆轴力变化较小.

1.2.2 高跨比β1与主缆轴力T1的关系

由图5可知，高跨比β1越大，主缆轴力T1越

1.2 矢跨比、高跨比与主缆轴力的关系

若主缆水平力越大，即主缆轴力越大，则整个结构刚度也越大，抵抗结构变形的能力越强，主缆轴力为：大；当β1＝0～0.4时，主跨径L＝600～1 000 m独塔悬索桥主缆轴力变化量不大.

由图4和图5可知，当矢跨比越小，高跨比越大时，主缆轴力越大，抵抗变形能力越强.为使结构具有较大的刚度，建议矢跨比取0.04～0.08，高跨比取0.2～0.4.

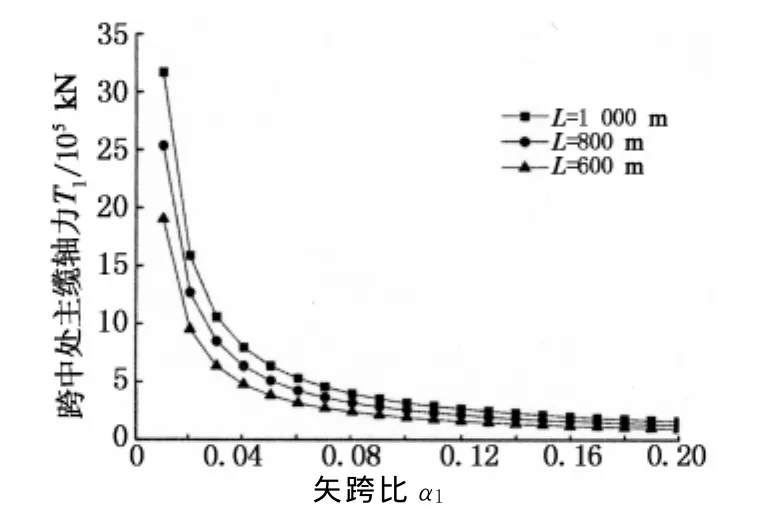
图4 矢跨比与主缆轴力的关系曲线Fig.4 Relation ofα1 and T1

图5 高跨比与主缆轴力的关系曲线Fig.5 Relation ofβ1 and T1

2 合理矢跨比、高跨比材料经济性研究

2.1 主跨主缆用钢量

主缆面积及主缆用量分别为［7］：

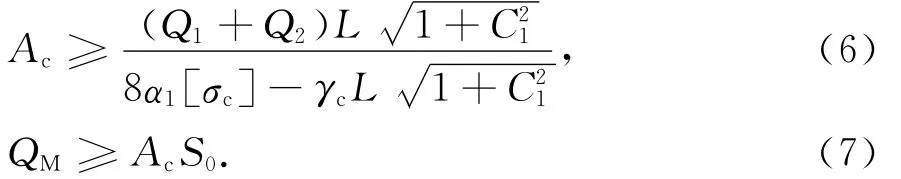
式中：C1＝4α1＋β1；α1＝f／L；［σc］为主缆容许应力；Q1为一期恒载集度；Q2为二期恒载集度；γc为主缆容重；S0为无应力索长.

2.2 矢跨比、高跨比与主缆用量的关系

若主跨跨径、材料弹性模量、主缆容重以及荷载集度均不变，主跨主缆用量只与主跨矢跨比α1和高跨比β1有关.下面分别对主跨径600～1 000 m的独塔悬索桥进行分析（计算采用Q1＝178.1 k N／m，Q2＝53.1 k N／m，［σc］＝500 MPa）.

2.2.1 矢跨比α1与主缆用量QM的关系

图6为矢跨比与主缆用量的关系曲线.由图6可知，当矢跨比为0.03～0.12时，主缆用量下降明显，跨径越大，主缆用量下降越快；当矢跨比为0.12～0.2时，曲线平缓，主缆用量变化较小.

图6 矢跨比与主缆用量的关系曲线Fig.6 Relation ofα1 and QM

2.2.2 高跨比β1与主缆用钢量QM的关系

图7为高跨比与主缆用钢量的关系曲线.由图7可知，高跨比越大，主缆用量越大，跨径越大，主缆用量增长越快，高跨比在0～0.16时，主缆用钢量相对较少.

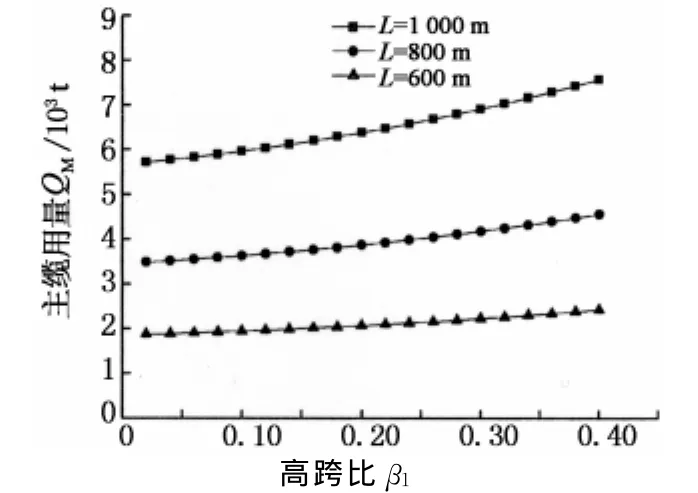
图7 高跨比与主缆用钢量的关系曲线Fig.7 Relation ofβ1 and QM

2.3 索塔材料用量Qt

由图8索塔受力示意图可推出［8］：

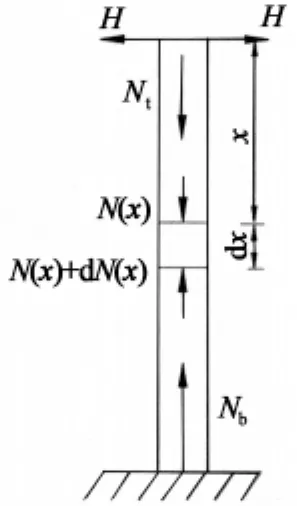
图8 索塔受力示意图Fig.8 Schematic of structural response of a tower

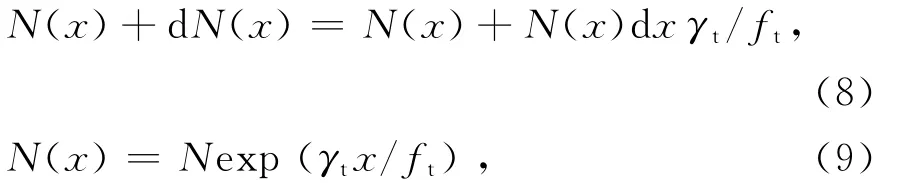
式中：γt为索塔容重；ht为索塔高度；ft为索塔容许应力；Nt＝H（tanφm＋tanφb），tanφm＝（C＋4f）／L，tanφb＝4fLb／L2＋Cb／Lb.

下面分析跨径为1 080 m，矢跨比为0.06～0.11，塔高为156～320 m的独塔双主跨悬索桥钢索塔用量的变化情况，以便了解矢跨比和塔高对索塔用量的影响.图9和图10分别为矢跨比、高跨比与索塔用量关系曲线.

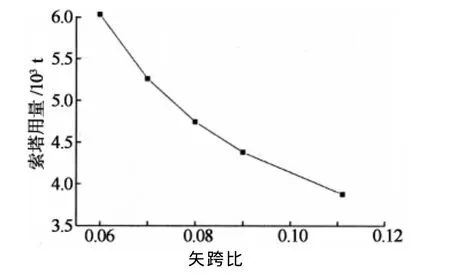
图9 矢跨比与索塔用量关系曲线Fig.9 Relation between rise-span ratio and value of tower

图10 高跨比与索塔用量关系曲线Fig.10 Relation between height-span ratio and value of tower

由图9和图10可知，矢跨比越大，索塔用量越小，塔高越高，索塔用量越大.主缆和索塔用量决定了独塔悬索桥的造价，通过前面的分析，为使结构具有经济性，建议矢跨比取0.12～0.2，高跨比取0～0.16.

3 材料经济性与结构合理性平衡范围

针对主跨跨径为600～1 000 m的独塔悬索桥，分别分析矢跨比α1，高跨比β1与主缆用钢量QM与主梁挠度值λ的关系，以寻求一个合理的α1，β1范围值使结构用量和刚度均较为合理.

由图11可知，主梁挠度值λ与矢跨比α1近似成线性关系，矢跨比α1越大，主梁挠度λ越大；当α1＝0～0.12时，主缆用钢量QM下降明显.

由图12可知，若高跨比β1越大，则主梁挠度λ越小；若主缆用钢量QM越大，主梁挠度和主缆用钢量变化值较小，则可认为高跨比β1对主梁挠度值和主缆用钢量影响不大.

通过对矢跨比和高跨比在结构经济性的研究和结构变形影响的研究，最终建议矢跨比α1＝0.07～0.12，高跨比β1＝0.14～0.24为合理范围.

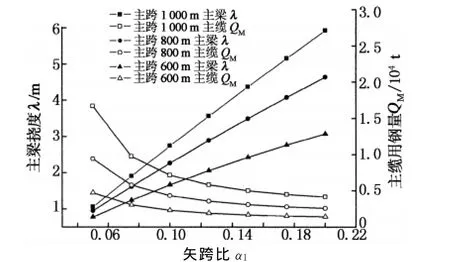
图11 α1与λ，QM关系曲线Fig.11 Relation amongα1，λand QM

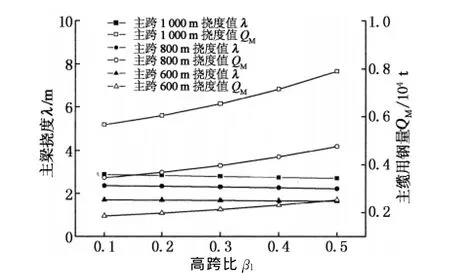
图12 β1与λ，QM关系曲线Fig.12 Relation amongβ1，λand QM

4 独塔悬索桥与三塔悬索桥比较算例

4.1 矢跨比与高跨比的选择

对跨径布置为1 080 m＋1 080 m的独塔双主跨悬索桥采用不同矢跨比（α1＝0.07～0.11）、高跨比（β1＝0.1～0.3）进行分析，结果见表1、表2和表3.

由表1可知，矢跨比越大，主缆用量和主缆水平力越小，索塔用量越大.与中国某三塔悬索桥（以下简称三塔悬索桥，见图13）相比，当α1＝0.07～0.11时，独塔悬索桥主缆用量和主缆水平力均大于三塔悬索桥.由表2可知，索塔高度相同，矢跨比越大，主缆和索塔用量以及主缆水平力越小.

比较表1和表2可知，相同矢跨比，索塔越高，独塔悬索桥主缆和索塔用量以及主缆水平力越大.

由表3可知，独塔悬索桥与三塔悬索桥矢跨比均为0.11时，索塔高度变化对独塔悬索桥主缆水平力影响较小，但对主缆和索塔用量影响较大，与三塔悬索桥相比，主缆最多可节省20%用量，索塔最多可节省83%用量.

通过上述分析，综合考虑结构经济性和结构受力性能，本文试设计的独塔悬索桥采用矢跨比α1＝0.11，高跨比β1＝0.2.

表1 不同矢跨比独塔悬索桥与三塔悬索桥各参数比较Tab.1 Results of a three-tower suspension bridge and single-tower suspension bridge in various rise-span ratios

表2 具有相同塔高的不同矢跨比独塔悬索桥与三塔悬索桥各参数比较Tab.2 Results of a three-tower suspension bridge and single-tower suspension bridge with various rise-span ratios and same height of tower

表3 不同塔高独塔悬索桥与三塔悬索桥各参数比较Tab.3 Result of a three-tower suspension bridge and single-tower suspension bridge in various height-span ratios

图13 某三塔悬索桥立面图（单位：m）Fig.13 Elevation view of three-towers suspension bridge（unit：m）

4.2 算例比较分析

试设计的独塔双主跨悬索桥（见图14），跨径布置为1 080 m＋1 080 m，主梁高3.5 m，全宽39.1 m，主缆矢跨比采用0.11，两主缆横向中心间距为34.8 m，主缆材料为极限抗拉强度为1670 MPa镀锌高强钢丝；吊杆布置间距为12 m，主梁上方吊杆采用柔性吊索，主梁下方吊杆采用刚性吊杆.加劲梁一、二期恒载与三塔悬索桥相同（一期恒载集度为178.1 k N／m，二期恒载集度为53.1 k N／m），桥面设计成双向6车道，汽车荷载等级为公路－I级.

图14 1 080 m独塔双主跨悬索桥方案（单位：m）Fig.14 Single-tower suspension bridge scheme with a main span of 1 080 m（unit：m）

4.2.1 结构使用性比较

主缆强度安全系数K＝2.53＞2.5，主缆与鞍槽之间摩擦系数μ＝0.2，主缆钢丝在鞍座槽内抗滑移安全系数K＝2.096 2＞2，钢塔塔顶纵向抗推刚度为28.5 MN／m，（三塔悬索桥抗滑移安全系数K＝2.019 7，中塔塔顶纵向抗推刚度为25.9 MN／m）.

1）钢塔受力分析.塔柱最大应力工况为一个主跨加基本可变荷载，另一个主跨不加载，塔柱关键截面应力计算结果比较见表4.

表4 塔柱应力结果比较Tab.4 Result of pylon’s stress MPa

由表4可知，在恒载＋活载作用下，独塔悬索桥索塔分叉点截面及塔底截面最大拉应力分别为69.7 MPa和31.1 MPa，最大压应力分别为－193.6 MPa和－191.4 MPa，分叉点截面应力幅为263.3 MPa，塔柱底部截面应力幅为222.5 MPa.从表4比较结果可知，关键截面最大拉、压应力值以及应力幅，独塔悬索桥均优于三塔悬索桥.

2）结构变形计算.主梁最大挠度及塔顶纵向最大位移工况均为不对称汽车活载加载，经计算分析，主梁在索塔位置处支撑体系设竖向限位挡块，不设竖向支座约束，纵向设弹性约束，横桥向设置抗风支座约束.表5为结构变形结果的比较.

表5 结构变形结果比较Tab.5 Result of structural deflection

由表5可知，独塔悬索桥最大塔顶位移为1.467 m，小于三塔悬索桥塔顶最大水平位移1.724 m，三塔悬索桥主梁最大挠跨比为1／259，主梁最大转角0.018，独塔悬索桥主梁最大挠跨比为1／308，主梁最大转角0.013.两桥主梁挠跨比均满足《公路悬索桥设计规范》（JJJ XXX－2002）规定汽车荷载（不计冲击力）引起的竖向挠度值不宜大于跨径的1／250～1／300的要求.相比之下，独塔悬索桥主梁挠度及最大转角较小均小于三塔悬索桥，因此，更能保证结构竖向刚度和行车条件.

4.2.2 材料经济性比较

本文试设计的独塔悬索桥主塔采用纵向刚度较大的人形钢塔，塔高266 m，塔柱斜腿中心交点以上塔柱高170 m，分叉点以下塔柱高96 m，下塔柱张开量为80 m，主塔结构采用Q370qd和Q420qd钢材，上塔柱壁厚60 mm，下塔柱壁厚40 mm，塔顶纵向宽度15 m直线变化到纵向宽度为20 m的分叉点截面，塔柱截面尺寸如图15所示，钢索塔用量合计约为16 504 t；三塔悬索桥钢中塔用量合计约为10 980 t，C50混凝土边塔用量为30 488 m3.目前钢塔造价约为1.5万元／t，混凝土塔造价约为3 000元／m3，三塔悬索桥索塔总造价约为25 614万元，独塔悬索桥钢塔造价约为24 756万元，三塔悬索桥索塔与独塔悬索桥索塔造价相差约为3.5%.

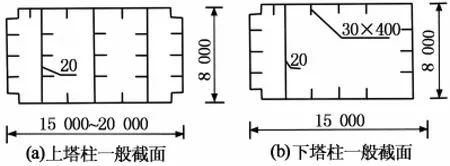
图15 塔柱截面示意图（单位：mm）Fig.15 Cross-section of pylon（unit：mm）

独塔悬索桥主缆无应力长度约为2 262 m，单根主缆面积为0.384 7 m2，主缆总用量约为13 666 t.三塔悬索桥主缆无应力长度约为3 100 m，单根主缆面积约为0.326 6 m2，主缆总用量约为15 886 t，试设计的独塔悬索桥主缆用量相对三塔悬索桥节省约14%.

4.2.3 通航及结构可实施性

从通航的角度，要求尽量减少桥墩的数量，或最好不设桥墩.一般情况下，长江公路大桥的通航净宽可以以《内河航道通航标准》代表船队中16×3 000 t级内河船队要求的主航单孔双向通航时通航净空宽度不小于600 m，通航净空高度以5 000 t级进江海轮控制的设计最高航水位时通航净空高度不小于24 m来判断设计桥梁是否满足通航要求.本算例所设计的独塔双主跨悬索桥为双主航道，单孔通航净宽可达415 m，通航净高可达50 m，均大于上述要求，可以满足正常情况下内河通航要求.

主缆位于主梁以下部分的构造可以通过在这个区域设置刚性吊杆，使与主梁下缘铰接，刚性吊杆与主缆之间通过索夹连接，刚性吊杆与索夹铰接，主梁以下的两主缆索夹可以考虑采用桁架或者框架结构将其连接以防止主缆横向摆动.

5 结 语

1）本文对独塔悬索桥基本性能进行初探，针对独塔悬索桥两个重要参数——矢跨比和高跨比进行研究，讨论了矢跨比和高跨比各自对结构用量和结构受力变形的影响，最后综合考虑结构经济性和结构刚度合理性，建议矢跨比α1＝0.07～0.12、高跨比β1＝0.14～0.24为合理范围.

2）为验证建议的矢跨比和高跨比可使结构具有经济性和使用性，本文试设计了一座独塔双主跨悬索桥进行了结构经济性和受力分析，并与中国某三塔悬索桥在结构经济性、结构变形和结构受力方面进行比较，经济性分析表明独塔悬索桥主缆用量约为三塔悬索桥主缆用量的86%，约可节省14%；独塔悬索桥钢塔造价约占三塔悬索桥索塔总造价的96.5%，约可节省3.5%，由此说明试设计的独塔悬索桥具有经济性.结构使用性方面独塔悬索桥塔柱最大拉、压应力值均小于容许应力，且小于三塔悬索桥钢中塔应力值，独塔悬索桥主梁最大挠跨比、主梁最大转角以及塔顶最大纵向位移均小于三塔悬索桥，更符合行车需要.

3）算例表明试设计的独塔悬索桥兼具材料经济性和结构使用性，并在一定程度上略优于中国某三塔悬索桥.因此，独塔悬索桥可使结构满足经济性和结构使用性的要求，并且可与三塔悬索桥方案进行比选.

［1］ JOHN S，RAFAL M，MARWAN N.Design of looping cable anchorage system for new San Francisco-Oakland Bay Bridge main suspension span［J］.Journal of Bridge Engineering，2002，7（6）：315－324.

［2］ 胡建华，陈冠雄，向建军，等.平胜大桥设计构思与创新技术［J］.桥梁建设，2006（2）：28－31.

HU Jian-hua，CHEN Guan-xiong，XIANG Jian-jun，etal.Design considerations and innovative techniques of pingsheng nndge［J］.Bridge Construction，2006（2）：28－31.（In Chinese）

［3］ 朱仲毅.独塔自锚式悬索桥恒载状态下结构线形及内力分析［J］.铁道科学与工程学报，2005，2（2）：46－50.

ZHU Zhong－yi.Analysis of the geometry and inner force for self-anchored suspension bridge with single-tower under dead load［J］.Journal of Railway Science and Engineering，2005，2（2）：46－50.（In Chinese）

［4］ NAZIR C P.Multi-span balanced suspension bridge［J］.Journal of Structure Engineering，1986，112（11）：2512－2527.

［5］ FUKUDA T.Analysis of multi-span suspension bridges［J］.Journal of Structure Division，1976，13（9）：63－86.

［6］ 李国豪.桥梁与结构理论研究［M］.上海：上海科学技术文献出版社，1983：1－12.

LI Guo-hao.Bridge and structure theory research［M］.Shanghai：Shanghai Science and Technology Literature Press，1983：1－12.（In Chinese）

［7］ 邵旭东.桥梁设计与计算［M］.北京：人民交通出版社，2007：691－722.

SHAO Xu-dong.Bridge design and computation［M］.Beijing：China Communications Press，2007：691－722.（In Chinese）

［8］ 尼尔森J吉姆辛.缆索支承桥梁：概念与设计［M］.金增洪，译.北京：人民交通出版社，2002：259－286.

NIELS J G.Cable supported bridge：concept and design［M］.Translated by JIN Zeng-hong.Beijing：China Communications Press，2002：259－286.（In Chinese）

Research on Suspension Bridges with a Single-tower

JIANG Wang，SHAO Xu-dong†，PENG Wang-hu，YU Jia-yong
（College of Civil Engineering，Hunan Univ，Changsha，Hunan 410082，China）

Based on the deflection theory and equal-substitute beam method，the reasonable rise-span ratio and height-span ratio were suggested.A single-tower suspension bridge was designed according to the proposed rise-span ratio and height-span ratio，and was compared with a three-tower suspension bridge.According to the results，the number of main cables and the tower＇s construction cost of a single-tower suspension bridge reduced by 14%and 3.5%，respectively，as compared with a three-tower suspension bridge.The ratio of deflection to span，the maximum rotation angle of the main girder and the longitudinal displacement of the tower top in a single-tower suspension bridge are lower than that computed for a threetower suspension bridge separately under live load.Therefore，a single-tower suspension bridge is more economical and competitive，compared with three-tower suspension bridges.

bridge engineering；single-tower suspension bridge；deflection theory；equal-substitute beam method；rise-span ratio；height-span ratio；three-tower suspension bridge

U448.25

A

1674-2974（2011）06-0013-07＊

2010-06-12

国家自然科学基金资助项目（50778071，50908083）

蒋 望（1983－），男，湖南宁远人，湖南大学博士研究生

†通讯联系人，E-mail：shaoxd＠vip.163.com