钢纤维含量对活性粉末混凝土抗疲劳性能的影响＊

方 志，向 宇，匡 镇，王常林

（1.湖南大学土木工程学院，湖南长沙 410082；2.湖南中大建设工程检测技术有限公司，湖南长沙 410205；3.中国人民解放军95259部队，广东广州 510000）

钢纤维含量对活性粉末混凝土抗疲劳性能的影响＊

方 志1†，向 宇1，匡 镇2，王常林3

（1.湖南大学土木工程学院，湖南长沙 410082；2.湖南中大建设工程检测技术有限公司，湖南长沙 410205；3.中国人民解放军95259部队，广东广州 510000）

通过对3种不同钢纤维含量的活性粉末混凝土（RPC）进行单向受压等幅疲劳试验，研究了钢纤维含量对其抗疲劳性能的影响.结果表明：在疲劳荷载作用下，素RPC的破坏形态表现为劈裂破坏，钢纤维含量分别为1.5%和3%的RPC都表现为剪切破坏.随钢纤维含量的提高，RPC的疲劳寿命和疲劳强度相应提高.其宏观损伤、ε-n／Nf曲线和疲劳变形模量的衰减均表现出3阶段规律，随钢纤维含量的提高，ε-n／Nf曲线第1阶段和第3阶段延长.对应相同的荷载循环比，疲劳变形模量随钢纤维含量的增大而显著提高.在RPC构件抗疲劳验算时，建议钢纤维含量分别为1.5%和3%时，疲劳弹性模量与初始弹性模量的比值分别取0.7和0.75.

疲劳性能；疲劳试验；活性粉末混凝土；钢纤维含量

活性粉末混凝土（Reactive Powder Concrete，RPC）是一种具有高强度、高耐久性及良好韧性的超高性能混凝土，具有广阔的研究与应用前景.若将这种高强材料应用于工程结构，将显著减小截面尺寸，减轻结构自重，使结构的活载应力幅明显提高，从而对其抗疲劳性能的研究将成为这种新型材料工程应用时关注的主要问题之一.作为一种超高性能钢纤维混凝土，RPC的力学性能必然服从钢纤维混凝土和高强混凝土类材料的一般规律.对钢纤维混凝土抗疲劳性能的研究，始于丹麦奥尔堡波兰特水泥与混凝土实验室，于1986年研制了疲劳极限约为0.58的中等含量钢纤维混凝土（CRC）.Naaman等［1－2］对钢纤维混凝土在压缩循环荷载作用下的性能进行了研究，钢纤维混凝土适合在承受动荷载的情况下工作，且即使带裂缝工作，疲劳极限也高达0.65.鞠扬等［3］对钢纤维体积率Vf＝1.2%的圆柱体试件进行了等幅和典型变幅压缩疲劳试验，发现了宏观疲劳损伤演变的“潜伏期”现象和“疲劳锻炼效应”.

对于高强混凝土的抗疲劳性能，Fergestad等［4］进行了高强混凝土疲劳试验，结果表明高强混凝土的疲劳极限低于普通混凝土，后者在14万次循环荷载下疲劳极限为0.55，而前者200万次循环荷载作用下的疲劳极限为0.47～0.52.吴佩刚等［5］也得到了类似的结论.

目前国内外对RPC材料配合比、强度、耐久性等方面研究较多［6－7］，但对其抗疲劳性能的研究少有文献报道.余自若等［8］研究了单一配比下RPC的抗疲劳性能，结果显示RPC的抗疲劳性能优于普通混凝土.基于目前材料静力性能的研究结果，可知钢纤维含量的提高能显著改善其静力性能，但对其抗疲劳性能的影响还未见相关文献报道.参考既有的普通混凝土和钢纤维混凝土疲劳性能研究成果［8－12］，本文对3种钢纤维含量（体积率分别为0%，1.5%，3%）的RPC试件进行疲劳试验，研究钢纤维含量对其抗疲劳性能的影响.

1 试验概况

1.1 原材料及配合比

RPC的配合比见表1.制备RPC主要材料为：水泥强度等级为42.5级的普通硅酸盐水泥；硅灰的平均粒径为0.1μm，SiO2质量分数＞90%；石英砂为40～70目精制石英砂，平均粒径0.23～0.45 mm；减水剂为可溶性聚羧酸系高效减水剂，当含固量为35%，掺量为2%时，减水率为25%以上；钢纤维为采用镀铜光面平直钢纤维，其直径为（0.16± 0.005）mm，长度为（12±1）mm，抗拉强度＞2 000 MPa.

为了研究钢纤维含量对RPC材料性能的影响，分别采用了0%，1.5%，3%3种不同的钢纤维含量.

试件分组及荷载参量如表2所示.

表1 RPC材料配合比Tab.1 Material ratio of RPC

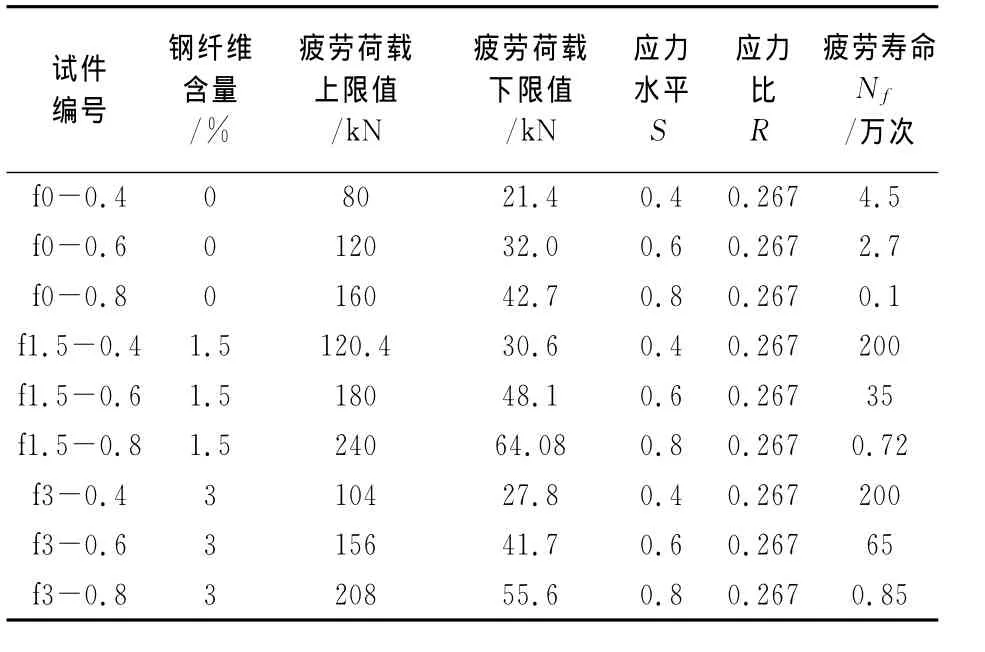
表2 荷载参量及试件疲劳寿命Tab.2 Load parameters and fatigue life of specimens

1.2 试件制备与养护

考虑试验机所能提供的最大荷载为500 k N，本文设计了两端截面较大（100 mm×100 mm），中部截面较小（50 mm×50 mm）的哑铃型试件用于RPC疲劳试验，试件形状及测点布置如图1所示.

图1 试件形状及测点布置图（单位：mm）Fig.1 Specimen shape and arrangement of measuring points（unit：mm）

同批制备尺寸为100 mm×100 mm×100 mm的立方体试件，100 mm×100 mm×400 mm的棱柱体试件和40 mm×40 mm×150 mm的抗折条形试件共计42个，用于测定RPC的静力性能.

试件浇筑完成先于标准养护室静置24 h后拆模，然后于80℃的热水中养护48 h，待自然冷却后，于室温环境下养护28 d.

1.3 试验方法

疲劳试验加载装置采用PMS-500数显式液压脉动疲劳试验机（见图2），加载频率为5 Hz，采用3种最大应力水平控制加载，分别为0.4，0.6和0.8来研究不同应力水平下RPC的抗疲劳性能.此处最大应力水平Smax是指施加的最大应力幅值σmax和试件的静载抗压强度fc之比，即Smax＝σmax／fc.其中fc于试验前取同种配比的3个哑铃型试件进行静载试验确定.对应3种不同的应力水平均取Smin＝0.267Smax.载荷历程采用正弦波谱.

图2 试验加载装置图Fig.2 Loading device of fatigue test

实测3种钢纤维含量RPC的28 d力学性能参数及哑铃型试件静载抗压强度fc如表3所示.

表3 试件材性参数表Tab.3 Material properties of specimens

2 试验结果分析

2.1 宏观损伤现象

RPC的宏观损伤过程按裂纹的演变模式分为裂纹潜伏阶段、裂纹稳定扩展阶段、失稳破坏阶段3个不同的阶段.根据钢纤维含量的不同，其破坏形态存在较大差异，当钢纤维含量分别为1.5%和3%时，宏观疲劳破坏表现为剪切破坏，而素RPC则表现为劈裂破坏.图3为根据试验现象绘制的疲劳加载过程中试件表面可视裂纹的演变示意图.

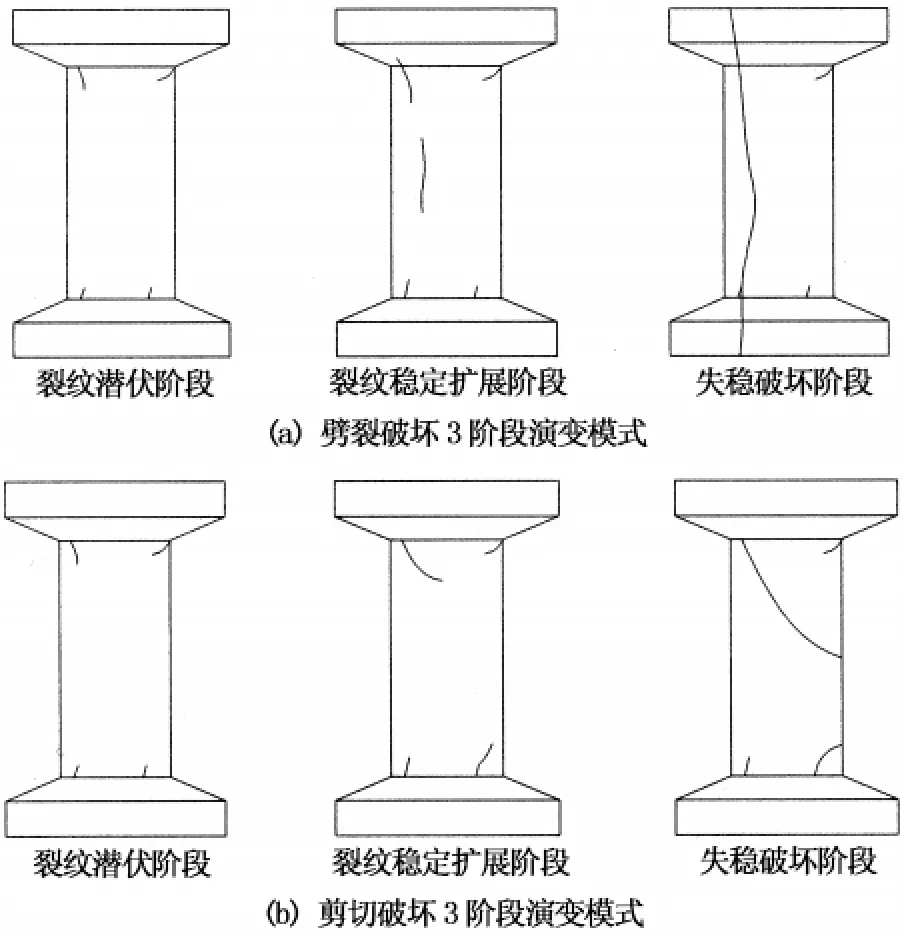
图3 RPC宏观裂纹3阶段演变模式Fig.3 Three-stage evolution model of macro cracks on RPC

第1阶段为裂纹潜伏阶段，试件上下两端出现数条竖向短裂纹，但随着荷载循环次数的增加，并不会迅速延伸，试件表面也未见其他裂纹萌生.实测表明，该阶段约占总疲劳寿命的15%左右.

第2阶段为裂纹稳定扩展阶段，此时随钢纤维含量不同表现出2种情况：其一，在试件中部出现一条纵向裂纹，并不断向两端延伸，最终形成贯通的纵向主裂缝（钢纤维含量为0%）；其二，第1阶段产生的端部纵向短裂缝沿约40度角向试件中部发展，裂纹长度和宽度稳定增加，最终形成剪切斜裂缝，该阶段约占总疲劳寿命的75%左右（钢纤维含量分别为1.5%和3%）.第3阶段为失稳破坏阶段，主裂纹迅速扩展直至贯通，试件丧失承载力，最终疲劳破坏，该阶段约占总疲劳寿命的10%左右.

2.2 疲劳寿命、疲劳方程及疲劳强度

2.2.1 疲劳寿命

疲劳寿命是指循环荷载作用下至试件破坏时的循环次数，本试验以2×106次作为疲劳强度对应寿命，当试件在某级循环荷载作用下达到2×106次时停止循环加载，进行疲劳后静载试验测定其力学性能的变化情况.

为反映疲劳寿命随钢纤维含量的变化规律，将各试件的疲劳寿命绘制成图4所示曲线，可见随着钢纤维含量的增加，RPC的疲劳寿命增大，随着应力水平的提高，RPC的疲劳寿命减少.

图4 疲劳寿命随钢纤维含量变化曲线Fig.4 Fatigue life-steel fiber ratio curves

2.2.2 双对数疲劳方程

根据本文疲劳试验的结果，应力水平S和疲劳寿命N的对数值lgS和lgN保持较好的线性关系，符合幂函数模型的特征，经回归分析给出双对数疲劳方程如表4所示.

表4 疲劳方程拟合计算表Tab.4 Calculation table of fatigue equation

由疲劳方程可绘制RPC应力水平S与疲劳寿命N的关系曲线如图5所示，由该曲线可估算各级应力水平对应的疲劳寿命，以及使试件免于疲劳破坏时的应力水平.

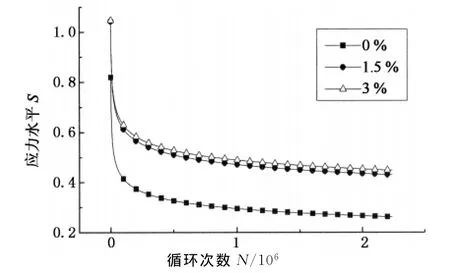
图5 3种钢纤维含量RPC的S-N曲线Fig.5 S-N curves of RPC with three types of steel fiber ratio

2.2.3 疲劳强度

疲劳强度是指材料在一定循环次数下能够承受的最大疲劳应力，结合S-N来说就是指寿命N趋于无穷大时所对应的应力水平S，在实际应用中通常用与静力强度之比的形式表示.对于混凝土类材料，常取N＝2×106作为疲劳极限寿命，并由表4中的方程分别计算得3种钢纤维含量RPC免于疲劳破坏的疲劳强度Sf，如表5所示.

表5 3种钢纤维含量RPC的疲劳强度汇总表Tab.5 Summary of the fatigue strength of the specimens

将文献［4］中得出的结论与本文试验结果（见表5）比较可知，钢纤维含量分别为1.5%与3%RPC的疲劳极限强度（分别为0.43与0.45）与高强混凝土的相应值（0.47～0.52）较为接近，但素RPC存在较大差异.林燕清等［12］对疲劳数据离散性进行了深入分析，认为混凝土强度的离散性是导致疲劳寿命及强度存在较大差异的主要原因.掺加钢纤维的RPC与素RPC相比，强度离散性相对较小，而素RPC强度的差异最大可达15%，这种误差将在混凝土疲劳试验中被急剧放大.

本文主要研究钢纤维含量对RPC抗疲劳性能的影响，尽管由于样本容量有限，试验数据存在一定的离散性，但3组数据之间相对变化的幅度仍然能够反映疲劳强度随钢纤维含量变化的一般规律.由表5可知，钢纤维的加入对于RPC疲劳强度的提高有显著的作用：钢纤维含量分别为1.5%和3%的RPC其疲劳强度分别比素RPC提高了59%和67%.疲劳强度随钢纤维含量的增加而提高，尤其是相对于素RPC而言，这种增强作用明显，但当钢纤维含量超过1.5%后，增强作用减弱.

2.3 变形特征

疲劳荷载作用下的试件变形，可以用应变－循环次数比（ε-n／Nf）曲线来描述.图6为不同应力水平下试件加载至最大应力σmax和卸载至最小应力σmin时纵向最大应变εmax和最小应变εmin随循环次数N的增加而变化的规律.

由图6可以看出，RPC纵向总应变（包括残余应变）随循环次数变化的一般规律符合“3阶段模式”：第1阶段纵向总应变发展较快，为内部损伤形成阶段，后期应变增长率随循环次数的增加逐渐降低；第2阶段，应变随循环次数的增加以接近恒定的增长速率变化，为内部损伤稳定扩展阶段；第3阶段，RPC的纵向总应变迅速增长，内部损伤加速发展，试件历经很短的时间循环后即产生突然的疲劳破坏.RPC疲劳变形过程曲线与普通混凝土相比有相似之处，但总体而言更加复杂，其特点是曲线受应力水平S和钢纤维含量的影响而呈现出不同的形状.

第1阶段所占比例随钢纤维含量的提高而增大（见表6），但提高幅度有限，该阶段混凝土基体尚未开裂，在循环荷载作用下，基体发挥主要作用，钢纤维辅之，所以其所占比例主要由基体性质决定，钢纤维含量对其影响并不明显.该阶段所占比例随应力水平的提高而增大，应力水平由0.6提高至0.8，第1阶段所占比例的平均值提高了21%.

图6 RPC疲劳应变－循环次数比曲线Fig.6 ε-n／Nf curves of RPC

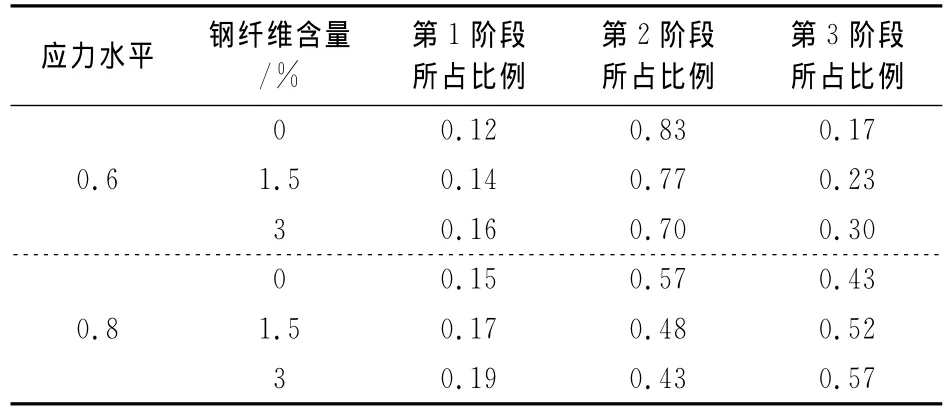
表6 疲劳应变－循环次数比曲线各阶段所占比例Tab.6 The proportion of each stage inε-n／Nf curves

第3阶段所占比例随钢纤维含量的提高而增大.通常认为该阶段的起点即为基体宏观裂纹的起始点，钢纤维含量越高，在基体开裂后越能有效地抑制裂缝的进一步扩展.在循环荷载作用下，通过纤维与基体的逐渐脱粘与纤维的逐渐拔出来消耗素RPC所不能消耗的额外能量，使得第3阶段的持续时间随钢纤维含量的提高而延长，在0.6的应力水平下，钢纤维含量分别为1.5%和3%的RPC与素RPC相比，第3阶段的所占比例分别提高了35%和76%，在0.8的应力水平下，钢纤维含量分别为1.5%和3%的RPC与素RPC相比，第3阶段的所占比例分别提高了20%和32%.该阶段所占比例随应力水平的提高而增大，应力水平由0.6提高至0.8，第3阶段所占比例的平均值提高了1.2倍.

钢纤维的添加显著延长了第1和第3阶段，相应第2阶段所占比例随钢纤维含量的提高反而减小，但该阶段长短主要由应力水平决定.钢纤维含量由0%提高至3%，该段所占比例最大降幅为25%（当应力水平为0.8时），而应力水平由0.6提高至0.8，3种RPC该段所占比例的平均值降低了36%，显然该值是随应力水平的增大而递减的，该结论与钢纤维混凝土压缩疲劳试验结果［7］保持一致.

2.4 疲劳变形模量

2.4.1 变形模量衰减曲线

混凝土单轴疲劳试验结果显示，纵向应变随荷载循环次数的增加不断增大，刚度逐渐退化.本文以试验所得RPC疲劳应力幅与应变幅之比来定义混凝土的瞬时变形模量（循环卸载点和再加载点的直线斜率为Ens），同时用第1次循环的疲劳变形模量E0s对瞬时疲劳变形模量Ens进行规范化，用疲劳寿命N对循环次数n进行规范化，即

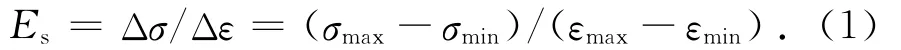
对图6所示的应变－循环次数曲线进行上述数学变换，得到疲劳变形模量随循环次数的变化规律，如图7所示.

图7 疲劳变形模量的变化曲线Fig.7 Fatigue deformation modulus curves

RPC疲劳变形模量随循环次数衰减的一般规律表现出3阶段特征：第1阶段疲劳变形模量随荷载循环次数的增加衰减较快，但该阶段只占疲劳寿命的15%左右，且衰减幅度较小；第2阶段疲劳变形模量随循环次数的增加以恒定的速率衰减，该阶段约占总寿命的75%；第3阶段为急剧不稳定的衰减，直至破坏，本阶段约占疲劳寿命的10%.

疲劳变形模量随钢纤维含量变化的规律为：在较低的应力水平（S＝0.6）作用下，对应相同的循环次数，变形模量随钢纤维含量的提高而提高.钢纤维含量较高的RPC，变形模量衰减曲线第1，2阶段较为平缓，第3阶段末的极限衰减率较高.为说明这一规律，表7给出了3种钢纤维含量的RPC试件在0.6和0.8两种最大应力水平下，疲劳变形模量的极限衰减率.

由表7可见，钢纤维含量对疲劳变形模量的影响显著，在相同应力水平下，变形模量的极限衰减率随钢纤维含量的提高而显著增大，钢纤维含量为3%的RPC比素RPC极限衰减率提高了38%，比钢纤维含量为1.5%的RPC提高了32%.

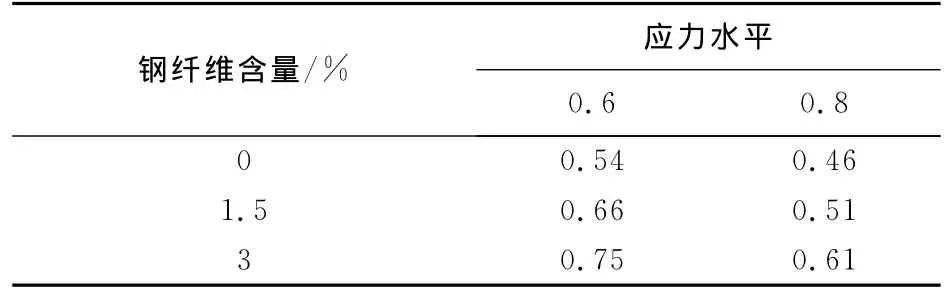
表7 疲劳变形模量的极限衰减率Tab.7 Ultimate decay rate of fatigue deformation modulus

疲劳变形模量随应力水平的变化规律为：应力水平越高，极限衰减率越小，以钢纤维含量为3%的RPC为例，应力水平由0.6提高至0.8，极限衰减率由0.75减小至0.51，衰减幅度达32%.

在较高的应力水平（S＝0.8）下，对应相同循环次数比，3种钢纤维含量的RPC变形模量接近，笔者认为由于应力水平较高，钢纤维的阻裂和增强作用已经不能表现出明显效果，其机理有待进一步研究.

2.4.2 疲劳后割线模量

本文疲劳试验中钢纤维含量分别为1.5%和3%的RPC试件在0.4的应力水平下经历200万次循环加载未破坏，停机进行静载试验至破坏，并给出应力－应变曲线，与疲劳试验前进行对照，结果如图8所示.

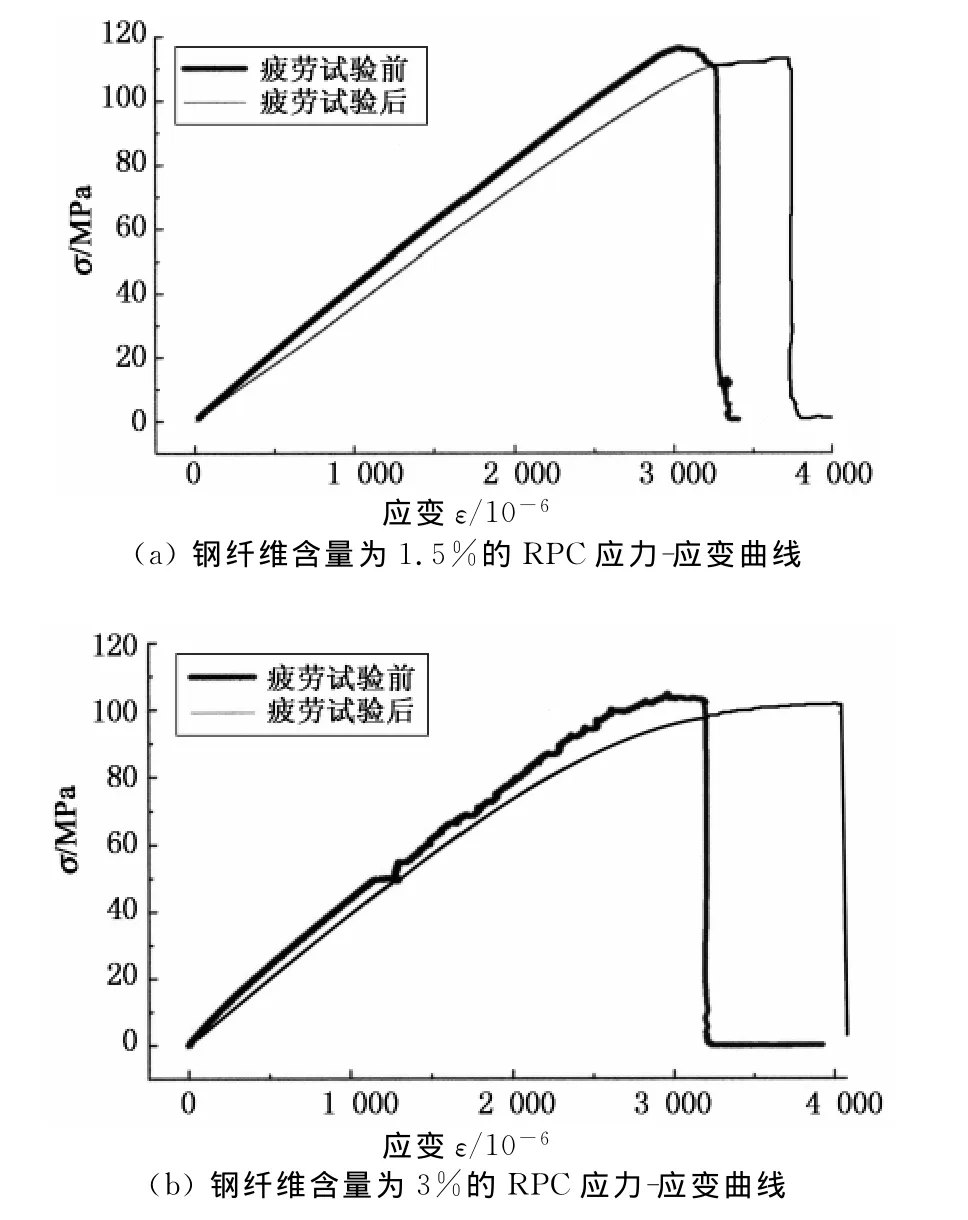
图8 疲劳后静载试验与初次静载应力－应变对比曲线Fig.8 Comparison chart of stress-strain curves before and after the fatigue test

表8为根据应力－应变曲线计算得出的钢纤维含量分别为1.5%和3%的2种RPC疲劳试验前后应力－应变曲线特征参量的汇总表.

表8 疲劳试验前后应力－应变曲线特征参量汇总表Tab.8 Characteristic parameters of stress-strain curves before and after the fatigue test

由表8可知，2种钢纤维含量的RPC经历200万次疲劳后，割线模量较疲劳试验前均呈现不同程度的衰减，其中钢纤维含量分别为1.5%和3%的RPC疲劳试验后割线模量与试验前相比，分别降低20%和25%，且随钢纤维含量的提高，疲劳后RPC的割线模量有降低趋势.

综合变形模量衰减曲线和疲劳后静载割线模量分析的结果，本文建议钢纤维含量分别为1.5%和3%的RPC经历200万次循环加载后，其疲劳弹性模量与初始弹性模量的比值，即Efc／Ec，分别取0.7和0.75，供RPC构件抗疲劳验算取用.

3 结 论

1）疲劳荷载作用下，素RPC的破坏形态表现为劈裂破坏，钢纤维含量分别为1.5%和3%的RPC则表现为剪切破坏.

2）随钢纤维含量的提高，RPC的疲劳寿命和疲劳强度相应提高.

3）RPC的宏观损伤，ε-n／Nf曲线和疲劳变形模量的衰减均表现出3阶段发展规律.随钢纤维含量的提高，ε-n／Nf曲线第1阶段和第3阶段延长；对应相同的荷载循环比，疲劳变形模量随钢纤维含量的增大而显著提高.

4）本文建议钢纤维含量分别为1.5%和3%的RPC其疲劳弹性模量与初始弹性模量的比值分别取0.7和0.75，供RPC构件抗疲劳验算取用.

5）钢纤维含量的提高对RPC的抗疲劳性能具有显著的增强作用.

［1］ OTTER D E，NAAMAN A E.Properties of steel fiber rein-forced concrete under cyclic loading［J］.ACI Materials Journal，1988，85（4）：254－261.

［2］ NAAMAN A E，HAMMOUD H.Fatigue characteristics of high performance fiber-reinforced concrete［J］.Cement and Concrete Composites，1998，20（5）：353－363.

［3］ 鞠扬，樊承谋.钢纤维混凝土的疲劳“锻炼效应”［J］.土木工程学报，1995，28（3）：66－71.

JU Yang，FAN Cheng-mou.Enhancement action in fatigue of steel fiber reinforced concrete［J］.China Civil Engineering Journal，1995，28（3）：66－71.（In Chinese）

［4］ FERGESTAD S，AMBJØR S.Raftsundet bridge in Lofoten，Norway［J］.SEI，1999，9（2）：96－99.

［5］ 吴佩刚，赵光仪，白利明.高强混凝土抗压疲劳性能研究［J］.土木工程学报，1994，27（3）：33－40.

WU Pei-gang，ZHAO Guang－yi，BAI Li-ming.Compression fatigue properties of high strength concrete［J］.China Civil Engineering Journal，1994，27（3）：33－40.（In Chinese）

［6］ RICHARD P.Composition of reactive powder concrete research［J］.Cement and Concrete Research，1995，25（7）：1501－1511.

［7］ 郑文忠，李莉.活性粉末混凝土配制及其配合比计算方法［J］.湖南大学学报：自然科学版，2009，36（2）：13－17.

ZHENG Wen-zhong，LI Li.Preparation and mix proportion calculation of reactive powder concrete［J］.Journal of Hunan University：Natural Sciences，2009，36（2）：13－17.（In Chinese）

［8］ 余自若，安名喆.活性粉末混凝土的疲劳性能试验研究［J］.中国铁道科学，2008，29（4）：63－70.

YU Zi-ruo，AN Ming-zhe.Experimental research on the fatigue performance of reactive powder concrete［J］.China Railway Science，2008，29（4）：63－70.（In Chinese）

［9］ 王瑞敏，赵国藩，宋玉普.混凝土的受压疲劳性能研究［J］.土木工程学报，1991，24（4）：38－47.

WANG Rui-min，ZHAO Guo-fan，SONG Yu-pu.Compression fatigue properties of concrete［J］.China Civil Engineering Journal，1991，24（4）：38－47.（In Chinese）

［10］李朝阳，宋玉普，赵国藩.混凝土疲劳残余应变性能研究［J］.大连理工大学学报，2001，41（3）：355－358.

LI Chao-yang，SONG Yu-pu，ZHAO Guo-fan.Study of residual strain of concrete under fatigue loading［J］.Journal of Dalian University of Technology，2001，41（3）：355－358.（In Chinese）

［11］欧阳辉，伍颖，杨军.钢纤维对混凝土疲劳性能增强的研究［J］.安全与环境工程，2004，11（1）：71－73.

OUYANG Hui，WU Ying，YANG Jun.Experimentation on fatigue behavior of steel fiber reinforced concrete［J］.Safety and Environmental Engineering，2004，11（1）：71－73.（In Chinese）

［12］林燕清，欧进萍.混凝土疲劳损伤试验中试件初始极限强度的推测方法［J］.哈尔滨建筑大学学报，1997，30（6）：9－20.

LIN Yang－qing，OU Jin-ping.A new method to infer the initial compressive strength of a single concrete specimen in its fatigue damage test［J］.Journal of Harbin University of Architecture and Engineering，1997，30（6）：9－20.（In Chinese）

Fatigue Properties of Reactive Powder Concrete with Different Steel Fiber Ratios

FANG Zhi1†，XIANG Yu1，KUANG Zhen2，WANG Chang-lin3
（1.College of Civil Engineering，Hunan Univ，Changsha，Hunan 410082，China；2.Hunan Zhongda Construction Engineering Testing Technology Co，Ltd，Changsha，Hunan 410205，China；3.The 95259 Force of Chinese PLA，Guangzhou，Guangdong 510000，China）

The fatigue properties of RPC（Reactive Powder Concrete）with different steel fiber ratios of 0%，1.5%and 3%in volume were investigated with the uniaxial compressive fatigue test.The results showed that the splitting failure mode appeared for pure RPC specimens without steel fiber，but the shear failure mode occurred for those specimens with steel fiber of 1.5%or 3%in volume.The fatigue life and strength increased with the increase of steel fiber ratio；the macroscopic damage，ε-n／Nfcurves and the evolution of the fatigue deformation modulus of tested RPC experienced three stages.With the increase of steel fiber ratio，the first and third stages ofε-n／Nfcurves lengthened，and the fatigue deformation modulus significantly increased with the increase of the steel fiber ratio corresponding to the samen／Nf.It is suggested that the ratio of fatigue deformation modulus to the initial elastic modulus should be 0.7 and 0.75 for the RPC with a steel fiber ratio of 1.5%and 3%，respectively.

fatigue properties；fatigue test；Reactive Powder Concrete（RPC）；steel fiber ratio

TU528.572

A

1674-2974（2011）06-0006-07＊

2010-10-20

国家自然科学基金资助项目（51078134）

方 志（1963－），男，湖北黄冈人，湖南大学教授，博士生导师

†通讯联系人，E-mail：zackfang＠163.com