连续配筋水泥混凝土路面温缩应力简化公式研究＊

白 桃，黄晓明，李 昶，林能辉，金 晶

（1.东南大学交通学院，江苏南京 210096；2.中国地震局工程力学研究所，黑龙江哈尔滨 150080）

连续配筋水泥混凝土路面温缩应力简化公式研究＊

白 桃1†，黄晓明1，李 昶1，林能辉2，金 晶1

（1.东南大学交通学院，江苏南京 210096；2.中国地震局工程力学研究所，黑龙江哈尔滨 150080）

连续配筋水泥混凝土路面（CRCP）在铺筑完成一段时间后，会在路面纵向上断裂成一个个单独的板块.借助正交设计和多元统计回归方法，在有限元计算的基础上，提出了单独板的温缩应力简化公式.极差分析结果表明，CRCP温缩应力影响因素的重要程度从大到小依次为：温度变化、裂缝间距、板厚、粘结刚度系数、钢筋直径、配筋间距.单因素单变量的回归分析，确定了温缩应力与各单个因素之间的大致关系.通过对各变量的假设组合分析，以单变量多因素的多元统计回归方法获得了一定精度的并能通过假设检验的拟合公式.误差分析表明，此公式的最大误差范围能控制在8%以内.

正交设计；连续配筋水泥混凝土路面；温缩应力；多元统计；简化公式

在水泥混凝土路面的温度应力计算中，通常将温度荷载简化为均匀温缩和梯度翘曲2个方面［1］.连续配筋水泥混凝土路面（CRCP）在铺筑完成一段时间后，板体裂隙发展会趋于稳定而在路面内形成一个个单独的板段.由于钢筋的存在，使得各板段不能像普通混凝土板一样自由伸缩而忽略温度均匀变化时的板体受力.因此，有必要对CRCP单个板体的均匀温缩应力进行研究.

1932年Vetter针对CRCP因混凝土干缩和温缩引起的钢筋受力状态进行了近似解析分析，给出了2种状态下最小配筋率的计算公式［1］.在近九十年的应用中，美国积累了大量的工程数据，建立了以AASHTO为代表的统计性经验方法［2］，并发展出一系列的CRCP设计方法和软件.但其建立过程不易查询得到，且这种经验性结论的应用有其局限性.陈云鹤［3］将连续配筋路面作为复合材料，利用复合材料力学等理论推导了连续配筋路面的温度应力，但其将配筋层等效为均质的薄夹层与实际不符.曹东伟［4］以杆单元处理钢筋，推导出了无地基摩阻和有地基摩阻2种情况下CRCP均匀温缩时板中应力计算公式，但是其结构比较复杂，应用不方便，并且，他假设混凝土横截面上的应力是均布的，与事实有一定的出入.

美国的典型设计方法AASHTO和NCHRP 1-15均以“punchout”作为设计极限状态［2］，前提是其国内连续配筋混凝土路面在经历或超过设计使用年限后已经出现了punchout.punchout极限状态设计中，环境温度的输入直接用来计算板体温度应力而不单独计算板体温缩应力.因此，鲜有单独针对CRCP温缩应力计算公式的研究.目前，中国连续配筋路面使用年限最长的也只有21年，都还没有达到CRCP设计使用年限，所以，以punchout为设计极限状态来研究中国的连续配筋路面不合适.从自主研究角度出发，针对CRCP的研究思路有借鉴普通水泥混凝土板研究方法的趋势，即将CRCP的受力划分为车轮荷载和温度荷载两块分别进行计算，再进行叠加.本文在有限元模型计算的基础上，借助正交设计和多元统计回归方法，提取CRCP均匀温缩应力计算的简化公式，为CRCP的受力计算提供参考，以方便工程应用.

1 计算模型及分析方法

本文选用ABAQUS有限元软件进行计算.在温度均匀变化情况下，一方面，钢筋与混凝土间的粘结刚度系数大约是地基摩阻系数的1 000倍，使得钢筋对板的约束要远大于地基；另一方面，CRCP的裂缝间距较小，减弱了温度降低所引起的温缩应力，因此地基摩阻力的变化在计算结果中很难体现，可忽略［4］.计算模型选用带单根钢筋的板条，不计入地基摩阻，由于对称性，取板条的一半进行研究，如图1所示.

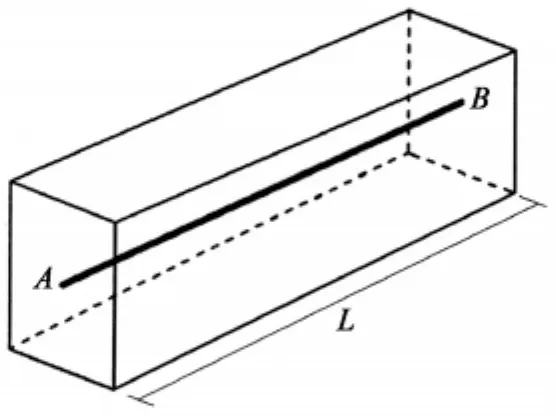
图1 带筋混凝土板条计算模型Fig.1 Model of reinforced concrete block

图1中，A端表示板中截面，B端表示裂缝端.钢筋选用truss单元里面的beam梁单元［5］，钢筋和混凝土的界面使用三向弹簧单元.即：默认钢筋和混凝土之间不产生垂直于钢筋轴向的挤入变形，横向刚度无穷大；而二者沿着钢筋轴向的剪切变形用弹簧受力变形来表征.粘结刚度系数Ks向弹簧刚度系数K的等效转换关系式为［6］：

式中：ds为钢筋直径，mm；L为计算板段长度，m；n为计算板段分段数.

计算过程中假定钢筋和混凝土均为弹性材料，各材料参数取值如表1所示.

表1 钢筋和混凝土材料参数Tab.1 Parameter values of steel and concrete

正交设计方法是一种处理多因素试验的科学试验方法，它利用规格化的正交表，合理地安排试验，通过较少次数的试验判断出较优的条件.若再对试验结果进行简单的统计分析，还可以更全面、更系统地掌握试验结果，做出正确判断［7］.正交试验设计的数据处理方法一般有极差分析法和方差分析法.

回归分析是一种处理变量与变量之间关系的数学统计方法，主要研究自变量变动对因变量变动的影响程度，其目的在于根据已知自变量的变异来估计或预测因变量的变异情况.在复杂的工程问题中，各因变量的相关关系及其显著性分析都因方程的非线性因素变得复杂，而多元回归分析使之变得简单.回归分析不仅能提供变量之间相关关系的准确表达式，判明所建立经验公式的有效性，而且能根据所得的经验公式，用一个或几个变量的值，预测或控制另一个变量的取值，达到一定的精度［8］.

2 因素影响分析

均匀温降情况下，CRCP板中温缩应力σc受到各种因素的影响.由于假定混凝土和钢筋均为弹性材料，模量和泊松比保持不变，则影响σc的因素主要有：板厚h、裂缝间距L、粘结刚度系数Ks、钢筋直径ds、配筋间距d和温度变化ΔT.为了考察σc与这6个变量之间的关系，本文采用正交设计方法，对每6个变量设置5个变化水平，见表2.

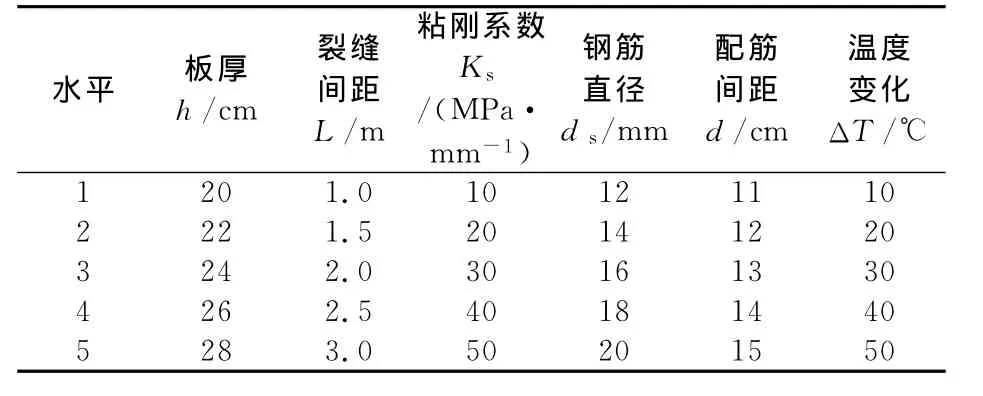
表2 6因素5水平正交设计表Tab.2 Six factors and five levels orthogonal design

以标准正交表L25（56）进行正交设计，正交表并计算结果见表3.

表3 L25（56）表CRCP的温缩应力正交分析Tab.3 Orthogonal analysis of CRCP’s contraction stress using table L25（56）

通过极差分析结果可以看出，影响CRCP温度应力的因素中，按重要程度依次为：温度变化＞裂缝间距＞板厚＞粘结刚度系数＞钢筋直径＞配筋间距.

此处各列均被因素、交互作用占满，试验误差无法估计，因此不进行方差分析.由于不知道回归公式中温度应力和各参量的对应形式，因此，先进行单因素单变量的回归分析，确定温度应力与各单个因素之间的大致关系.然后在此基础上，通过假设，对各变量进行组合分析，获得一定精度并能通过假设检验的拟合公式.

现行《公路水泥混凝土路面设计规范》（JTG D40－2002）［9］规定了连续配筋混凝土纵向钢筋计算参数经验参考值，见表4.

表4 纵向钢筋计算参数经验值Tab.4 Parameters’empirical value in longitudinal reinforcement calculation

考虑到粘结刚度系数可变性很小、与温缩应力回归关系的相关性不强，并且在后续的6因素回归分析中，回归公式无法通过假设检验.因此，将粘结刚度系数取定34 MPa／mm，然后进行其他5变量的组合回归分析.

3 回归分析

3.1 单变量单因素回归

取单板条模型，每次固定其中4个因素的值，单独变化余下一个因素的取值，计算温缩应力以获取其与各单个因素之间的对应关系.各组合的因素取值见表5，计算结果绘制的散点图并趋势线回归如图2～图6所示.其中应力取值为板中底部的纵向拉应力.

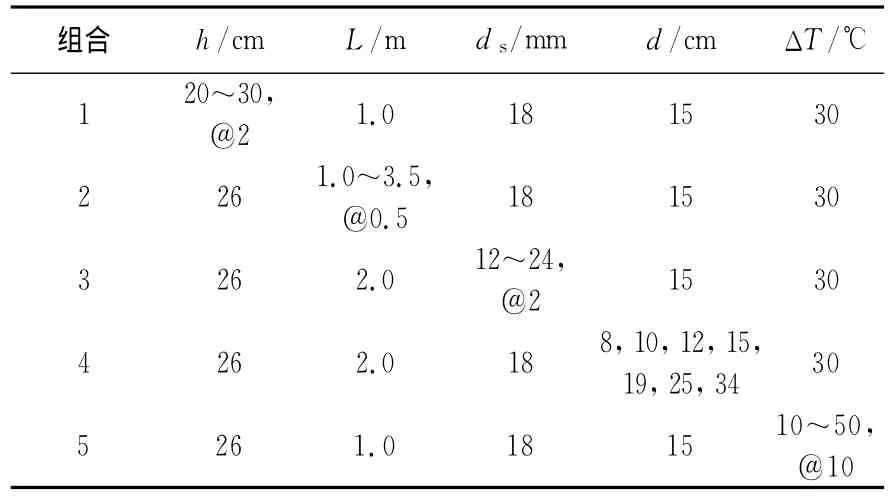
表5 单因素分析中参数取值Tab.5 Parameter value in the single factor analysis

图2 板厚与温缩应力散点图Fig.2 Scatter diagram of thermal stress and plate thickness

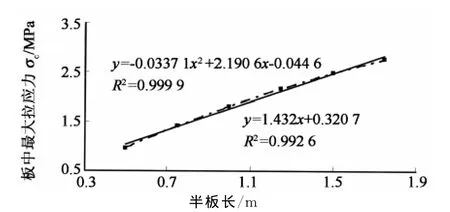
图3 板长与温缩应力散点回归关系图Fig.3 Scatter diagram of thermal stress and plate length

图4 钢筋直径与温缩应力散点回归关系图Fig.4 Scatter diagram of thermal stress and bar diameter

图5 钢筋间距与温缩应力散点回归关系图Fig.5 Scatter diagram of thermal stress and bar spacing

图6 温度变化与温缩应力散点回归关系图Fig.6 Scatter diagram of thermal stress and temperature change

3.2 单变量多因素回归

根据上节各因素与σc的回归关系，并从回归公式简易性表达出发，假设σc与d和h服从幂指数关系，而与L，ds和ΔT之间服从线性关系.如此，则先将L，ds和ΔT3因素合并考虑，即

总之，本研究揭示了江西南昌地区女性的大样本宫颈HPV感染现况及年龄特点，为南昌地区宫颈癌的二级预防提供了必要的流行病学数据，对宫颈癌疫苗的接种工作具有一定的参考意义。

式中：R为中间变量；β0，β1和β2分别为回归系数.

保证d＝15 cm和h＝26 cm不变，对板长L，钢筋直径ds和温度变化ΔT进行L9（34）正交表设计，结果见表6.

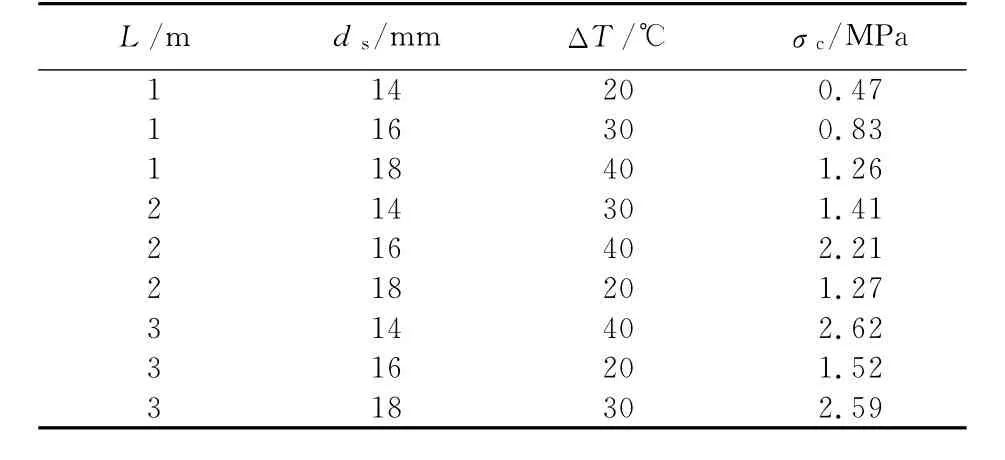
表6 L9（34）3变量正交设计Tab.6 Three-variable orthogonal design using table L9（34）

分别进行线性回归、二次和三次逐步回归，过程中预置95%的可信度，假设检验如表7所示.

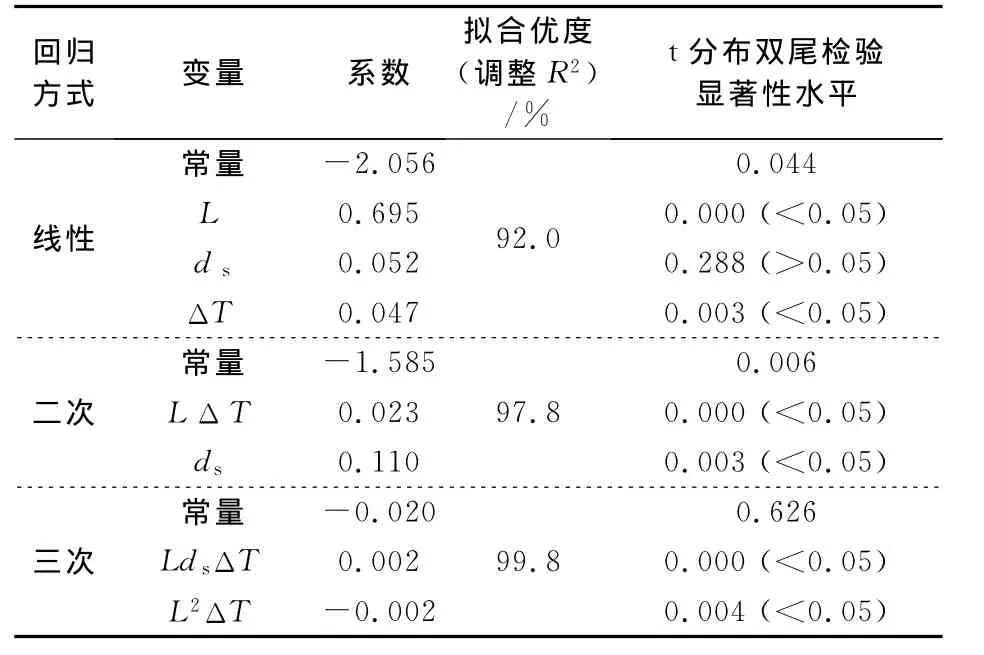
表7 3变量回归假设检验Tab.7 Three-variable regression hypothesis testing

从表7可以看出，三次回归所得的方程式简单、拟合优度高，并且能通过系数的t检验.其式为：

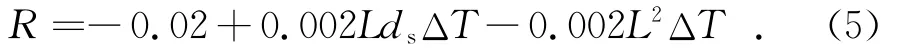
类似于表3，将其中的Ks变化栏全取定为34 MPa／mm，其他参数不变，重新进行混凝土板内的温缩应力计算，结果如表8所示.

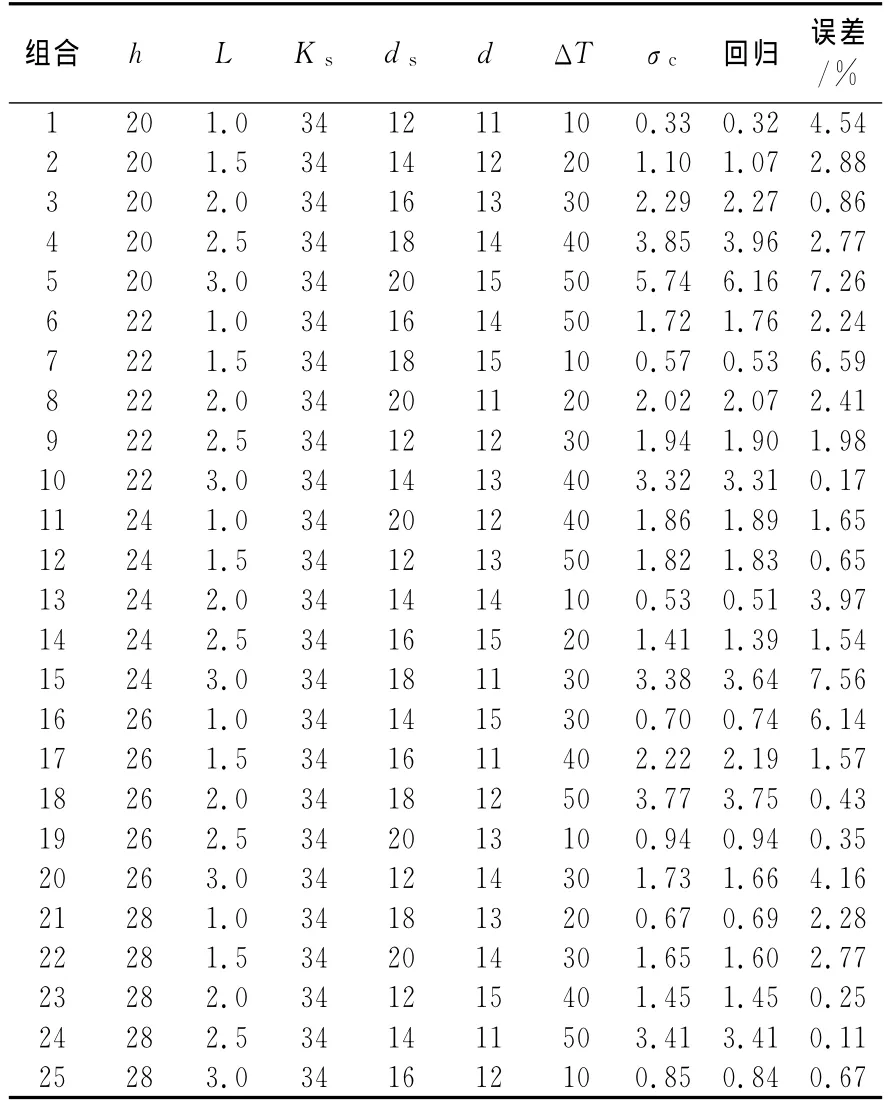
表8 定Ks的L25（56）CRCP温缩应力正交分析Tab.8 Orthogonal analysis of CRCP′S contraction tress using table L25（56）as Ks is fixed

最终得到的温缩应力回归公式为：

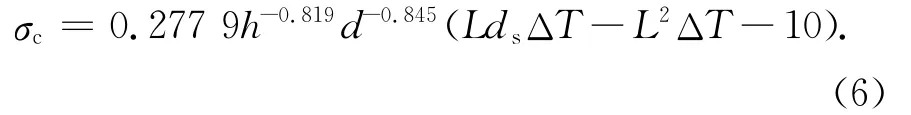
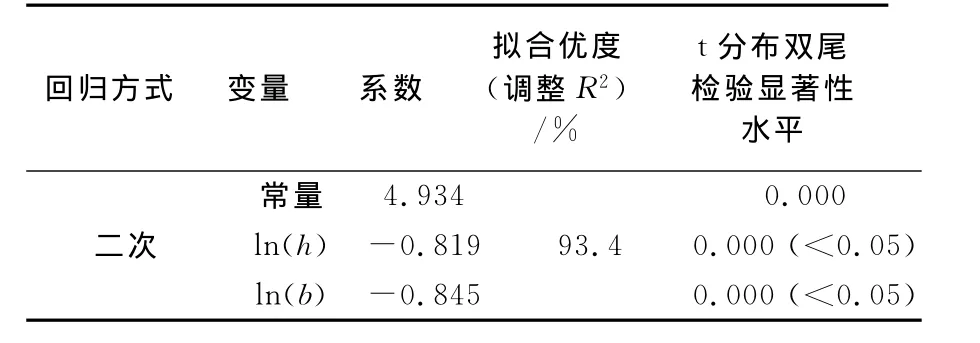
表9 h，b和R 3变量回归的假设检验Tab.9 Three-variable（h，b，R）regression hypothesis testing

4 公式验证

由于无法取得实测数据进行验证，本文选定粘结刚度系数为34 MPa／mm，然后任选3个因素组合并计算，得公式验证表如表10所示.

表10 公式验证表Tab.10 Formula verification

5 结 论

本文在有限元模拟计算的基础上，借助正交设计和多元统计回归方法，进行了连续配筋水泥混凝土路面温缩应力的简化公式研究.

1）提出了一种明确的简化公式提取思路和方法，可以为类似研究提供参考.

2）正交设计极差分析认为，影响CRCP温度应力的因素中，按重要程度依次为：温度变化＞裂缝间距＞板厚＞粘结刚度系数＞钢筋直径＞配筋间距.

3）以单变量单因素回归获得了混凝土应力和各因素之间的单一回归关系.然后在假设组合的基础上通过单变量多因素回归分析得到了CRCP板中温缩应力回归公式，此公式考虑了板厚h、裂缝间距L、钢筋直径ds、配筋间距d和温度变化ΔT5个影响因素.误差分析表明，此公式最大的误差范围控制在8%以内，精度足够高.

［1］ 邓学均，陈荣生.刚性路面设计［M］.2版.北京：中国人民交通出版社，2005：104－118；427－430.

DENG Xue-jun，CHEN Rong-sheng.Rigid pavement design［M］.2nd ed.Beijing：China Communications Press，2005：104－118；427－430.（In Chinese）

［2］ Mechanistic-Empirical Design Guide 2002.APPENDIX L L.Punchouts in continuously reinforced concrete pavements［S］.Illinois：ARA，Inc，ERES Division 505 West University Avenue Champaign，2003.

［3］ 陈云鹤.连续配筋混凝土路面荷载应力温度应力的计算理论与方法［D］.南京：东南大学交通学院，1999：57－66.

CHEN Yun-he.Calculating theory and method for load stress，thermal stress in continuously reinforced concrete pavement［D］.Nanjing：Transportation College，Southeast University，1999：57－66.（In Chinese）

［4］ 曹东伟.连续配筋混凝土路面结构研究［D］.西安：长安大学公路学院，2001：26－51.

CAO Dong-wei.Research on continuously reinforced concrete pavement structure［D］.Xi’an：School of Highway，Chang’an University，2001：26－51.（In Chinese）

［5］ Hibbitt，Karlsson ＆Sorensen Inc.ABAQUS analysis user＇s manual［M／CD］.Providence Rhode Island，USA：ABAQUS Inc，2006.

［6］ 白桃，黄晓明，李昶，等.均匀温降下连续配筋混凝土路面受力分析［J］.武汉理工大学学报，2010，32（7），55－59.

BAI Tao，HUANG Xiao-ming，LI Chang，etal.Mechanics analysis of CRCP under uniform temperature drop condition［J］.Journal of Wuhan University of Technology，2010，32（7），55－59.（In Chinese）

［7］ 高允彦.正交及回归试验设计方法［M］.北京：冶金工业出版社，1988：17－20.

GAO Yun-yan.Orthogonal and regression experimental design method［M］.Beijing：Metallurgical Industry Press，1988：17－20.（In Chinese）

［8］ 华伯泉.简明数理统计学［M］.天津：天津人民出版社，1987：243－245.

HUA Bo-quan.Concise mathematical statistics［M］.Tianjin：Tianjin People Press，1987：243－245.（In Chinese）

［9］ 中华人民共和国行业标准.JTG D40－2002 公路水泥混凝土路面设计规范［S］.北京：人民交通出版社，2003：53.

The Professional Standards of People′s Republic of China.JTG D40－2002 Design specification of cement concrete pavement design for highway［S］.Beijing：China Communications Press，2003：53.（In Chinese）

Simplified Formula Research on the Temperature Contraction Stress of Continuously Reinforced Concrete Pavement

BAI Tao1†，HUANG Xiao-ming1，LI Chang1，LIN Neng-hui2，JIN Jing1
（1.School of Transportation，Southeast Univ，Nanjing，Jiangsu 210096，China；2.Institute of Engineering Mechanics，China Earthquake Administration，Harbin，Heilongjiang 150080，China）

Continuously reinforced concrete pavement（CRCP）will break into separate slabs in the longitudinal direction a few months after its construction.Based on the calculation results of finite element method（FEM），a simplified formula of separate slab＇s temperature contraction stress was established by means of orthogonal design and multivariate statistical regression.Range analysis of the calculation results ranked the factors in the order of importance as follows：temperature change，crack spacing，slab thickness，bond-slip stiffness coefficient，bar diameter and bar spacing.Through single-factor and single-variable regression analysis，the general relationship between the temperature contraction stress and each factor was determined.A fitting formula was then obtained by single-variable and multi-factor multivariate statistical regression method through the assumption and combination analysis of each variable.The formula passed the hypothesis test，and error analysis showed that its maximum error range was controlled within 8%.

orthogonal designs；Continuously Reinforced Concrete Pavement（CRCP）；temperature contraction stress；multivariate statistical regression；simplified formula

U416.216

A

1674-2974（2011）06-0001-05＊

2010-07-24

交通部西部交通建设科技资助项目（6721001049）

白 桃（1987－），男，湖北洪湖人，东南大学博士研究生

†通讯联系人，E-mail：yixiaotian0113＠126.com