混合扩频测控体制下高精度测速研究

施 磊，苟先太，草 婷，吴 潜

（①西南交通大学电气工程学院，四川 成都 610031；②中国西南电子技术研究所，四川 成都 650000）

0 引言

混合扩频(DS/FH)体制在通信领域已经有了较为成熟的应用，但在航天测控领域的应用具有特殊性。低信噪比、高动态范围、大多普勒条件下的伪码快速捕获技术是测控系统与扩频通信系统之间的主要差别之一，DS/FH信号的快速同步捕获与多普勒偏移估计技术是十分关键的[1]。

1 宽带快跳系统快速同步技术

根据DS/FH测控体制的测速要求，一跳与一跳之间的多普勒频移量并不一样，所以在一跳的时间间隙内就要估算出该跳的多普勒频移量，这就对测控系统的测速时间提出了更高的要求。DS /FH的捕获包括跳频频点，直扩伪码和载波频率的三维捕获[1]。

1.1 传统载波多普勒频移跟踪方法

文献[2]给出了最大似然估计(MLE)和改进算法。该方法的主要思想是在时延和多普勒频移构成的二维坐标平面上求似然函数的最大值，以此来估计时延和多普勒偏移估计。

文献[3]给出了自适应最小均方误差算法(ALS)。该方法充分利用最小二乘的思想，并利用泰勒展开式来逼近变化的频率，有精度高且能适应快速变化载波的优点。

文献[4]给出了自适应频率跟踪环(AFC)，处理很大的多普勒偏移，通过划分频率区间的方法下变频，再利用 AFC环路对残留频偏进行捕获。但是该方法在多普勒偏移达到100kHz左右时，AFC环路难以有效工作。

文献[5]给出了基于扩张卡尔曼滤波器(EKF)的频率估计算法，该算法具有实时运算的优势，且能得到最小线性均方误差，但是该算法需要测量噪声信息和系统噪声信息，这使得系统需要很多的先验数据。

捕获载波的算法有很多种，评估算法的指标要综合估计精度、速度、工作环境信噪比、运算时间复杂度和硬件耗费等方面。

1.2 匹配快速傅里叶(PM-FFT)变换

[6]。考虑到无法保证跳频间隙内相位的连续性，故把分析的信号定义为相位随时间为非线性变化的信号，且不论时间的指数是整数或者分数。

有限时长信号 f(t)的FFT变换[7]可以表示为：

PM-FFT变换可以理解为在新的时间域(t2)里表示的FFT变换：

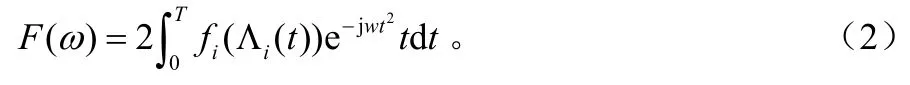
考虑到每一跳信号的相位变化规律都是有可能不相同，故用式(3)分析是不够的，由此给出匹配FFT变换的更一般形式，如式(3)：

式(3)中，Λi(t)是目标与地面相对运动决定的径向时间函数，ξ(t)是PM-FFT变换时设定的时间函数，该函数的约束条件是定义区间内，其导数必须均大于零或其导数必须均小于零。由此，给出PM-FFT变换的定义为：

若函数 f(t)在t的区域[0,T]内有定义且连续，ξ(t)导数连续且一只大于零或者小于零则有：

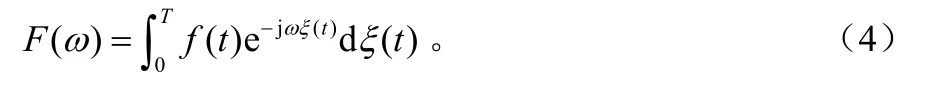
跳频信号时非常复杂的，比较简单情况是信号的相位中不仅有时间的二次方，还有时间的一次方，时间的一次方就是固定频率项，而固定频率项的存在会影响信号的PM-FFT变换谱[7]。处理二次方项需要二步PM-FFT变换，将时间一次方项和时间二次方项分别处理，二步PM-FFT变换不在这里进行讨论。

2 频谱细化方法

频谱细化方法参考文献[9]。

2.1 Z变换频谱细化方法

定义时间序列x(n)(0≤n≤N−1),其Z变换为：

A0,W0为正实数，给定A0,W0,θ0和ϕ0，当r=0,1,…,∞时，可得到在z平面上的点z0,z1,…,z∞，取这些点的Z变化，有

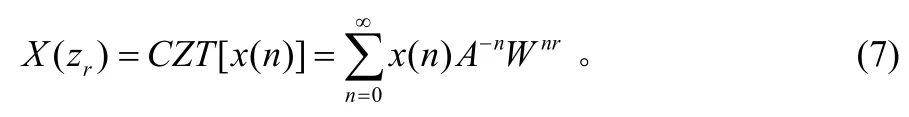
2.2 “栅栏效应”频率插值校正方法

参考文献[10]。当FFT频率分辨率不是实际频率的整数倍时，就会产生所谓的“栅栏效应”导致的频谱泄露问题，造成频率估计的误差，所以需要采用插值算法。较经典的由Quinn提出的利用FFT主瓣内，次大谱线和最大谱线FFT系数复数值之比的实部进行频率插值的方法，该算法结果如图1所示。

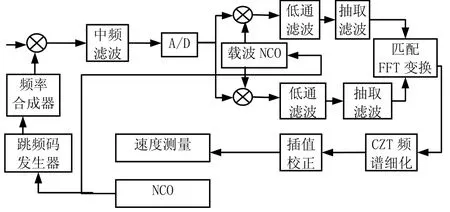
图1 算法结构

3 算法原理和仿真结果

低通滤波器的带宽应大于载波的最大偏移量（仿真最大多普勒偏移量为150 kHz），以允许大部分信号能量通过。抽取滤波器的抽取因子为100。

系统输入的中频信号为5 MHz的频率，多普勒频偏范围为±150 kHz，采样频率为1 MHz，信号通过抽取滤波器后采样频率降为了1 MHz，然后进行4 096点的FFT变化，频偏估计精度为1 MHz/4 096=244 Hz。取系统输入信号载噪比（C/N）为0。多普勒频移为0.5 MHz时的信号频谱图如图2所示。

图2 FFT检测到的频率量（局部）

由图3可以看出，当多普勒偏移为+0.5 MHz值时，峰值出现在第384点，估计出频偏值为0.507 3 MHz，如图4所示。而当多普勒偏移为-0.5 MHz值时，峰值出现在3 712点，估计出频偏值为-0.507 3 MHz，如图5所示。

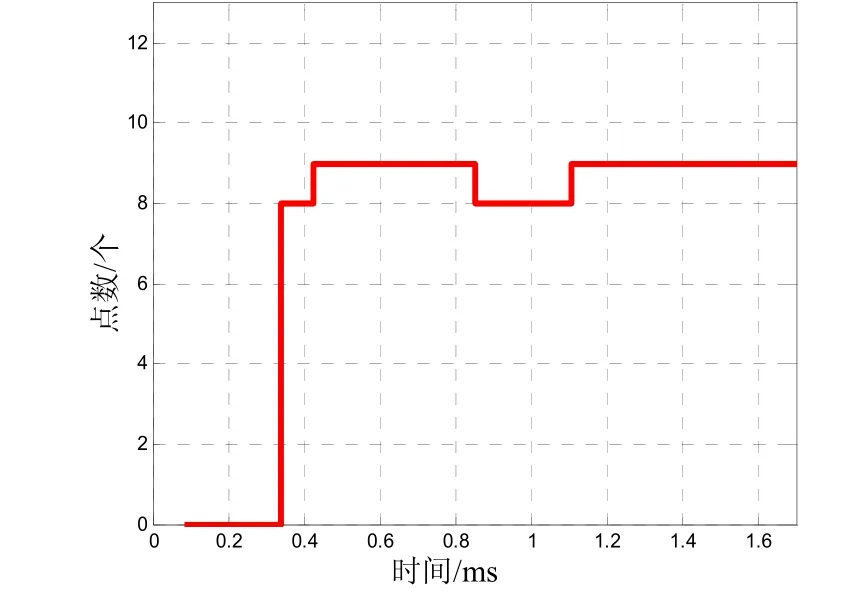
图3 计算用时间和点数

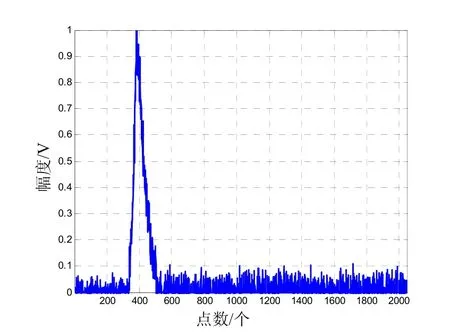
图4 多普勒偏移为正

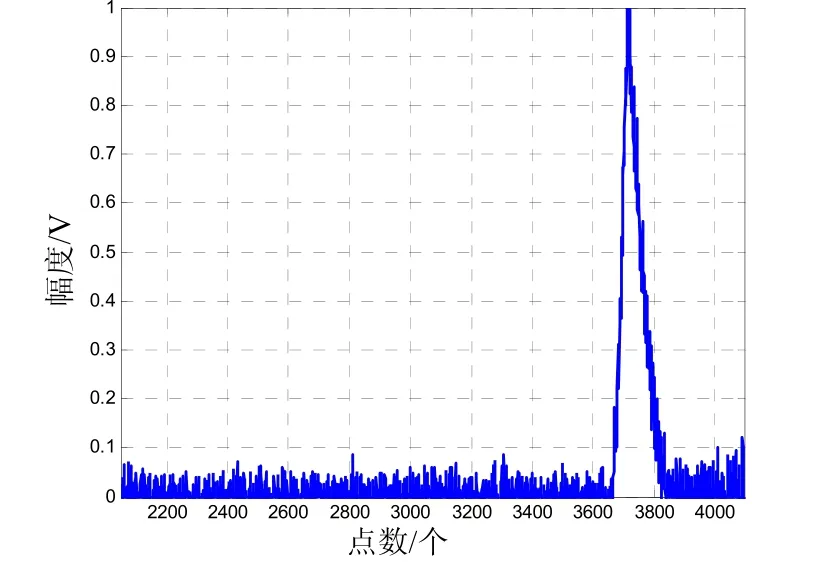
图5 多普勒频率为负

由图3可以看出，多普勒偏移的估算时间为0.085 ms，如果按照FH每秒10 000跳来计算，每跳驻留的时间为1/10 000=10 ms.FFT算法在时间上能够达到测速的要求。由以上分析已知，频率分辨率精度为244 Hz，每一次计算测速的精度为0.22 m/s，基本满足C频段的测控要求。

4 结语

在研究了 DS-FH/MSK测控体制下高精度测速方法的基础上，通过仿真表明了给出的采用匹配FFT技术对载波进行粗估计，再采用FFT频谱细化算法对载波多普勒频移进行精估计，并在较短的时间内同步系统的同时，对多普勒偏移进行高精度的估计和补偿的方法，应用于测控DS/FH测控的可能性，与传统方法相比较该方法在计算多普勒偏移时具有较大的时间效率，针对快速跳频系统每跳驻留时间较短和相位不一致的问题给出了具体的解决方案。另外还可以采用部分匹配滤波器的改进算法来进一步减少计算量，采用其它的插值变换来提高测量精度。

参考文献

[1] 苟先太.大多普勒频移下 DS/FH混合扩频测控机理与方法研究[J].学术动态，2010(02): 16-18.

[2] 杨光宣,苟先太,张波,等.DS/FH混合扩频快速同步技术研究[J].通信技术，2010,43(06):26-28.

[3] RIFE D C.Single Tone Parameter Estimation from Discrete-time Observations[J].Information Theory, 1974,20(05):591-598.

[4] NATION F D.AFC Tracking Algorithms[J].Communications,1984,8(32):935-947.

[5] HINEDI S.Two Novel Automatic Frequency Tracking Loops[J].Aerospace and Electronic Systems, 1989(25):749-760.

[6] KAPLAN E D.Understanding GPS Principles and Applications[M].USA: Artech House, 2006.

[7] 张波,杨光宣,金炜东,等.一种基于混沌码的宽间隔跳频图案实现[J].通信技术,2010,43(06):43-44.

[8] AKOPIAN D, AGAIAN S.Fast-matched Filters in Time Domain for GPS Receivers[J].IEE Proceedings Radar, Sonar and Navigation,2006, 163(06):525-531.

[9] 黄玉春,黄载禄,黄本雄,等.基于线性调频 Z变换的高性能频率估计[J].华中科技大学学报:然科学版, 2008, 36(06): 73-76.

[10] JANE V K, COLLINS W L, DAVIS D C.High-accuracy Analog Measurements Via Interpolated FFT[J].IEEE Trans-M,2009,28(02): 113-122.