基于虚拟基线的干涉仪测向改进方法

崔 旭

（中国电子科技集团第三十研究所保密通信重点实验室，四川 成都 610041）

0 引言

数字式相位干涉仪是一项对辐射源实施测向定位的技术，具备测向精度高、测角范围宽、适应辐射源信号能力强、天线布阵灵活、结构相对简单和技术体制成熟等特点，具有较强的工程实用价值，在信息战/电子战无源探测、交通管制、无线电频谱管理等军民用领域有着广阔的应用前景。

干涉仪基本的天线阵列为一维线阵，通常采用多个天线阵元构成多基线的配置形式，并且长短基线配合使用，长基线保证测向精度，短基线用于解相位模糊[1]。在某些特殊的工程应用场合，由于环境对天线尺寸和安装条件的限制，且短基线要求两阵元的间距小于辐射源信号的二分之一波长，当干涉仪工作在较高频段时，短基线间距太小难以布设，并存在互耦影响，导致多基线天线阵列工程实现难度较大。

现以一维线阵数字相位干涉仪为基础，通过多长基线系统构造虚拟基线作为短基线，完成相位解模糊，并对基于时域鉴相的测向估计方法进行改进，实现高精度测向。

1 相位干涉仪测向原理

数字干涉仪测向系统实际上是利用相邻阵元由于辐射源信号到达阵元的波程差而产生相位差，由相位差来进行到达角（DOA）计算。单基线测向原理如图1所示。

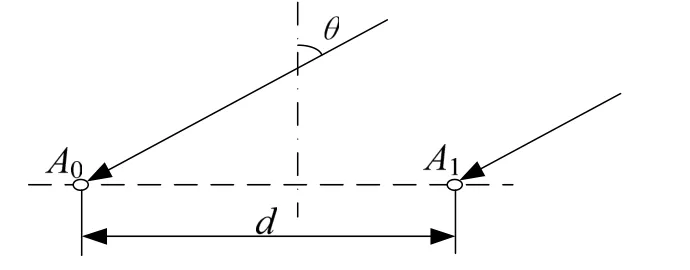
图1 单基线相位干涉仪

若有一平面电磁波从天线视轴(等强信号方向)夹角为 θ的方向到达天线阵元 A0、A1,则两天线接收到的信号相位差为：

式中, λ为辐射源的信号波长; d为两天线阵元间距; φ为信号到达两天线阵元的相位差。式（1）经变换，得:

式（2）即为辐射源到达角的基本计算公式。式中，若d ＞ λ/2是，相位差φ可能会大于2π，出现相位多值模糊。

构建多基线相位干涉仪系统时，通常需要利用短基线（d＜λ/2）解决相位模糊问题。同时，为保证高精度测向，必需设计较长的基线，以一维三基线相位干涉仪为例，原理如图2所示。

图2 多基线相位干涉仪原理

图中，由四个阵元 A0、A1、A2和 A3构成三条基线，长度分别为d1、d2和d3。其中，d3为最长基线，保证测向精度；d1为短基线，与d2配合用于逐次解相位模糊。根据式（1），可得：

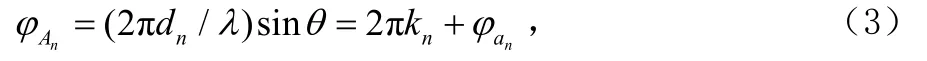
式中，kn≤dn/λ，n=1,2,3。φAn是不同基线dn的相位干涉仪产生的相位差，φan则为观测值。通过方程联立，根据基线比值，可以确定kn值，并由得到k3求得φA3，根据公式（2）计算出到达角θ，该θ值为该多基线相位干涉仪的最高精度测角值。

2 虚拟基线相位干涉仪测向原理

在工程应用中，若采用长短基线配对使用的多基线干涉仪系统，由于d1值一般比较小，尤其在对高频段辐射源测向时，首先天线架设和安装比较困难，其次天线阵元太近可能会带来天线互耦现象。若采用多长基线系统（无短基线），主要问题集中在解模糊的问题上，目前常采用的解决方法有两种：

①余弦定理解模糊方法；

②基于基线比多组相位差解模糊方法。

该两种方法在算法性能相当，满足一般的测向要求，但均存在缺陷[2]。①方法1要求基线比互质，解模糊时求整数解对鉴相误差比较敏感；②方法2算法较为复杂，需要进行多维搜索运算。两种方法存在同样问题：多基线系统需要多组基线比条件实现解模糊，一般地，当阵元数≥5个，才能保证测向精度。在对天线阵列有尺寸限制的应用场合，多长基线系统并不适合。

这里，构造了一种非对称三元直线阵，采用虚拟阵元的办法来构造虚拟短基线，达到解模糊，从而实现测向，原理如图3。

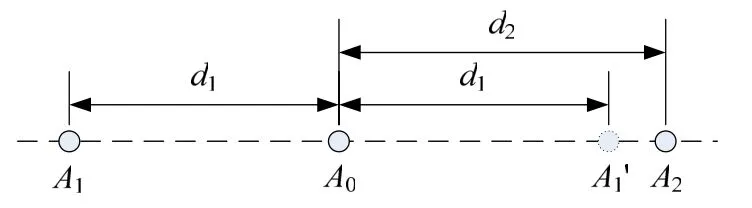
图3 非对称的虚拟阵元干涉仪

天线阵布置如图3所示。图中，A0为相位参考阵元，A1和A2关于A0非对称布置，而A1'为 A1关于A0对称的虚拟阵元，对于天线阵各基线长度的基本约束条件为：

①d2＞d1＞,均为长基线设置，保证测向精度；

②d2−d1＜，构造虚拟短基线，实现相位解模糊。

测向处理流程大致如下：

①以A0为参考阵元，计算A0A1和A0A2的相位差φ01和φ02，此时该相位差均为模糊值；

②根据φ01构造 A1关于A0对称的虚拟阵元A1'的相位差值φ0′1；

③变换以 A2为参考阵元，以φ02和φ0′1计算 A2A1'的相位差φ2′1值，此时该值为非模糊值（不考虑由于前面计算所得相位差模糊值关于值边界的模糊误差）；

④根据基本的干涉仪测向原理，利用A0A1'A2组建长短基线系统，A2A1'为短基线用于解模糊，A1'A0为长基线可实现测量来波关于干涉仪基线法线方向−9 0°～ 90°的方位角。

该方法与传统的长短基线测向原理相似，测向性能基本相当。

3 测向估计方法改进

数字相位干涉仪测向通常采用基于相位差解模糊的 DOA估计算法，为提高测向精度,可采用基于余弦估值误差方差最小准则的DOA估计算法进行性能优化，解模糊概率能提高大概5 dB[3]。但该种方法多适用于多长基线系统，测向性能对基线长度和数目均有一定要求。

基于虚拟基线的相位干涉仪系统在天线规模受限时，测向性能的提升从消除测向数字计算误差入手。DOA估值算法的核心是鉴相方法，鉴相误差直接影响测向精度。鉴相方法包括时域鉴相和频域鉴相，在高信噪比条件下，两种方法性能相当，在低信噪比条件下，频域鉴相的性能较优[4]。频域相对时域鉴相的性能提升，主要体现在窄带滤波和误差平均的效果上，频域鉴相方法性能与频谱变换后的频率分辨力有直接关系，对信号采样率有一定要求。在针对高速测向或采集数据有限的背景下，时域测向方法仍有相当的适用价值，数据处理更加灵活。

若两阵元的相位差为 φAn，时域鉴相方法是对信号相位差进行累积平均，即：

式中，N为时域采样数据长度。时域测向方法在信噪比条件下性能较差是由相位差估计值的最大绝对误差导致。根据公式（3），误差来自解模糊的kn确定，由此，测向精度的改进可通过kn对φAn(m)的数据进行筛选获得。

处理过程大致如下：

①对时域采样数据进行逐点求相位差，得到短基线无模糊相位差φan(m)，进行解模糊计算，得到kn(m)；

②利用大树判决准则，从集合kn(m) 确定标准值；

③对kn(m)进行筛选，条件为，得到新的解模糊无偏系数集合；

由上，改进方法主要通过大数判决准则确定解模糊无偏系数，以此为标准尽量去除鉴相误差较大的数据，从而筛选出“非弱段”数据进行测向估计，保证测向精度。

4 仿真分析

信号调制样式：单音；信号载频：1.2 GHz；采样率：100 MHz；采样点数：1 000；测向阵采用虚拟基线三元线阵布置，如图3，d1=0.5m，d2=0.6m。

假定辐射源到达角为25°条件下，分别用基本的数字相位干涉仪方法和改进方法进行测向估计。仿真软件：Matlab；仿真次数：1 000次。得到测向性能曲线如图4。

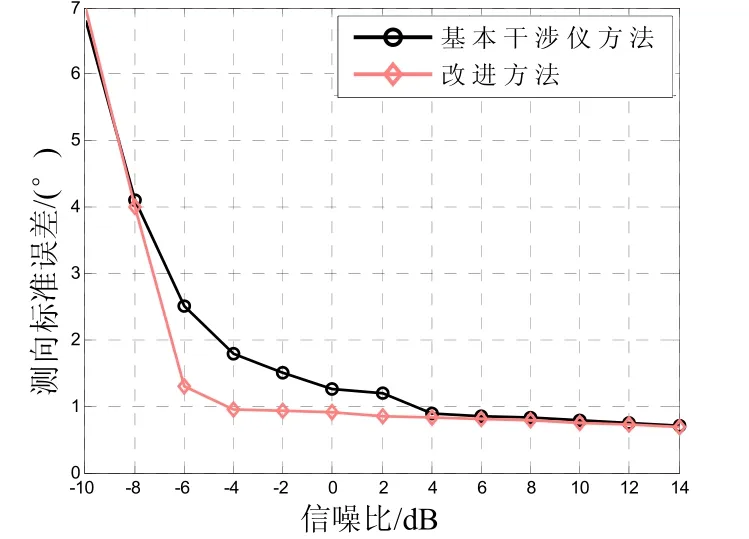
图4 测向性能仿真曲线

取辐射源达到角为10°、45°时，性能曲线趋势基本相似。通过基本干涉仪方法和改进方法的对比可以得到：

①改进方法在信噪比条件较高时，与基本干涉仪的测向性能相当；

②随着信噪比条件的降低，基本干涉仪方法的测向性能逐渐下降并迅速恶化，而改进方法在大数判决条件满足时仍能保持测向精度。但当信噪比条件恶化至一定程度，导致大数判决条件不成立，改进方法性能退化至与基本干涉仪一样。

5 结语

根据数字相位干涉仪原理，给出一种基于虚拟基线的数字相位干涉仪方法，能够解决测向精度和相位解模糊的矛盾，可消除了天线阵极小间距的限制；并通过从时域鉴相数据优化筛选，利用大数判决准则对干涉仪测向方法进行改进，可获得测向性能的改善和提升。理论分析与仿真验证了基于虚拟基线的数字相位干涉仪测向及改进方法的有效性，表明对于非弱段信号的测向，性能提升较为明显。基于虚拟基线的数字相位干涉仪及改进方法在工程上有着较强的实用前景。该方法能够应用在多长基线和不同天线阵形式的干涉仪系统中，测向性能可进一步得到提高。

[1] 袁孝康.相位干涉仪测向定位研究[J].上海航天, 1999(03):1-7.

[2] 龚享铱, 袁俊泉, 苏令华.基于相位干涉仪阵列多组解模糊的波达角估计算法研究[J].电子与信息学报, 2006, 28(01):55-59.

[3] 魏合文, 王军, 叶尚福.一种基于余弦函数的相位干涉仪阵列 DOA估计算法[J].电子与信息学报, 2007, 29(11):2665-2668.

[4] 李莉, 朱伟强.数字干涉仪测向实时鉴相技术[J].航天电子对抗,2005, 21(02):51-52.

[5] 蒋学金, 高遐, 沈扬.一种多基线相位干涉仪设计方法[J].电子信息对抗基数, 2008, 23(04):39-45.