改进的基于RSSI差值的定位算法

王振强，朱义胜

(大连海事大学，辽宁 大连 116023)

0 引言

目前，移动终端定位算法主要包括[1]：小区识别码（CI）定位，小区识别码和到达时延（CI+TA）定位和多基站质心定位。CI定位对手机没有特殊要求，采用基站的扇形覆盖中心作为终端的估计位置。CI+TA定位是对CI定位的改进，它将基站覆盖扇形区域中由TA所决定的550米宽度环形的中心作为终端的估计位置。多基站质心定位首先得到测量报告中的所有基站的位置，然后求这些位置的中心，作为终端位置的估计。这些定位方法的优势是所有手机和网络均支持，技术简单，系统成本低，因此在测量报告(MR)分析中，得到广泛应用。然而，这些定位方法的定位精度不高，达不到某些应用场合的要求。因此，大量的研究者致力于提高移动终端的定位精度，提出了各种有效的定位算法。

文献[2]提出了根据RSSI差值定位的方法，该方法将MR中的基站两两结合为一组，根据每个分组两基站的 RSSI差值分别画出一个圆，用这些圆的交点的中心作为手机位置的估计。文献[3]给出了最大似然法求解基于TOA（到达时延）差值的定位方程组的方法，给出了较高的定位精度。文献[4]给出泰勒法求解多点定位的方法，根据TOA估计终端位置。Liu Bo-Chieh[5]提出了一种方法来消除接收强度差（SSSD）中的测量误差。文献[6]改进了文献[4]中初始值的选择。文献[7]讨论了文献[3]的误差。

现借助多年GSM移动通信网络优化经验，改进了利用接收强度（RSSI）值的差进行定位的算法。该方法根据电波传播模型计算出基站和手机之间的距离，利用距离差建立线性方程组求解移动终端的位置。该文在求解方程组时考虑了距离测量和计算误差，并使用加权最小二乘法(WLS)两次求解，从而消除了距离误差对定位结果的影响，因而提高了估计精度。

1 基于RSSI差值的定位算法

以GSM网络为例，手机在通话过程中，每隔480 ms向基站控制器（BSC）上报一次测量报告。测量报告的内容包括[8]：服务小区的RSSI和TA（到达时延），6个最强邻区的RSSI。将这7个接收强度测量值代入电波传播模型，可以得出移动终端到每个基站的距离估计，进而通过求解方程组，得出移动终端的位置估计。如图1所示，以3个基站为例，在直角坐标系中，手机的位置坐标为 MS(x0,y0)，BS1、BS2、BS3为三个基站，它们的位置坐标分别为(x1, y1)、(x2,y2)、(x3, y3)，则手机的坐标与基站的坐标符合方程组（1）：

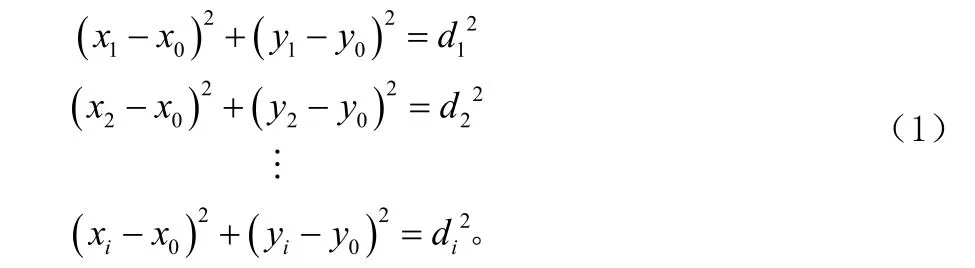
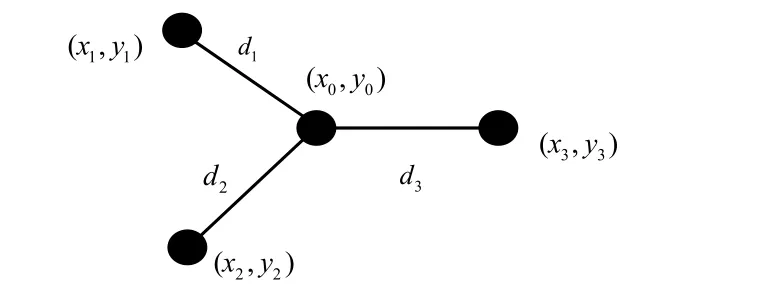
图1 手机定位算法示意

方程组（1）是一个非线性方程组，如果参与定位基站大于等于 3个，该方程组是超定的。借鉴文献[3]的方法，采用加权最小二乘法(WLS)求解超定方程组（1），详细求解过程如下：

①分别用后面的方程减去第一个方程，可以将上述方程组简化成线性方程组，即：

②如果参与定位的基站数等于3个，则上述方程的解为：

A−1表示A的逆，如果参与定位的基站数大于3个，可以采用最小二乘法来求解，其解为：

AT表示A的转置，A−1表示A的逆；

③进一步考虑到误差，则方程可表示为：

ψ为误差向量，参照文献[3]，使用加权最小二乘法可以得出，方程组（5）的解为：

这里，Ψ是ψ协方差矩阵，从式（2）、式（5）可以得出：

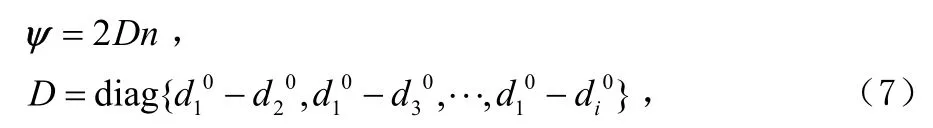
其中，Ψ是ψ的协方差矩阵，Q是距离测量误差n的协方差矩阵。因为Ψ中包含了手机终端与基站间的真实距离，这里无法得到。为了求解方程组，必须进一步假设，这里先假设D ≈d0I ，I为单位矩阵，d0为统一的距离差，因此由（6）式可以得到（9）式。

这里,Q是距离测量误差n的协方差矩阵,参照文献[4],距离测量误差定义如下：

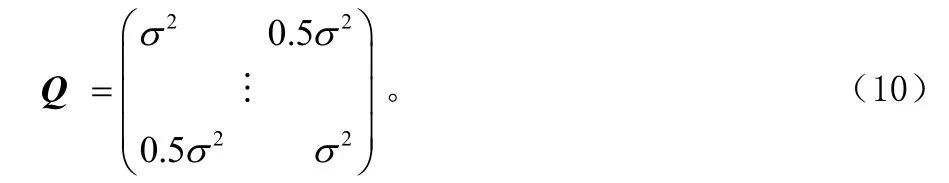
这里，σ为距离测量标准差。试验证明，多数情况下，用式（9）得出的定位精度已经足够，如果想进一步提高精度，可以用式（9）计算出初步位置，然后将式（9）结果代入式（8）求出Ψ，最后用式（6）得出最后定位结果。

2 传播距离的计算

在方程组（1）中，di表示基站i与终端之间的距离，要从接收强度测量值计算出距离di，需要借助无线电波传播公式。一般采用经验公式，这里采用广泛使用的 COST231模型[9-10]，结合试验区域的场景，确定了相关传播模型参数。

根据COST231模型，无线传播损耗Lb由三部分组成，即：

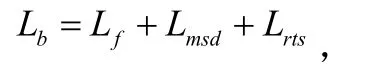
其中，Lf表示自由空间损耗，Lmsd表示由于连排房屋引起的多重障碍屏绕射损耗，Lrts表示从屋顶到路面的绕射损耗。

这里，平均街道宽度w为 20米，基站和平均屋顶高度差Δhb为8米，屋顶和手机终端的高度差Δhm为16米，则路径损耗Lb可以简化为下式：

对于900 MHz频段：

对于1800 MHz频段：

根据文献[6]，GSM基站的有效全向辐射功率（EIRP）为56.4 dBm。从而，手机在某点接收到基站的信号场强I，可以用式(13)表示：

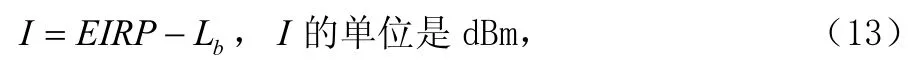
因此，对于900MHz频段：

对于1 800 MHz频段：

3 定位结果对比

为验证改进的基于RSSI差值定位方法的定位精度，以某运营商GSM网络为基础设计了一个定位精度试验。试验选取了某城区2 km×0.5 km的长方形区域作为定位测试评估区域，该区域有 10个基站，基站间的平均距离为 700米，平均街道宽度w为20米，基站和平均屋顶高度差Δhb为8米，屋顶和手机终端的高度差Δhm为16米。使用GPS定位设备及测试手机和测试软件进行 DT测试，同时收集MR数据。

从测试数据中提取测量报告中的RSSI和TA等定位基础数据，将基站的经纬度变换成平面直角坐标，然后根据式（6）计算出终端的初步估计位置，再进一步用式（9）计算出精确的估计位置。这里，取2σ=18。为了评估定位精度，这里把估计位置和终端真实位置的距离偏差作为定位误差，把67%和 95%的测试样本所能达到的定位精度作为评价算法优劣的标准。该文将此改进算法与CI、CI+TA和质心定位三种方法进行了定位精度对比。结果表明改进后的 RSSI差值定位的精度远高于CI+TA定位。当参与定位的基站数量为6时，基于RSSI差值的定位方法可以达到E911二阶段定位精度要求。应用改进 RSSI差值方法进行定位，参与定位的基站数量越多，定位误差越小，定位精度越高。图2给出各种定位方法的定位误差CDF分布，很明显，RSSI差值定位的精度远高于CI和CI+TA定位。但RSSI差值定位要求参与定位的基站数量最小为3个，而CI和CI+TA定位对参与基站的数量无要求。

图2 定位误差的CDF比较

表1给出了改进的RSSI差值定位与质心定位的定位误差对比。其中，其中RSSI(6)一列给出了使用改进算法定位，且参与定位的基站数为6时的定位精度，其他依次类推；质心(6) 一列给出了使用质心算法定位，且参与定位的基站数为6时的定位精度，其他依次类推。可以看出，参与定位基站数量在3～6之间时，RSSI定位的平均精度均高于质心定位。当基站数为6和5时，改进RSSI差值定位算法的定位精度均值提高幅度较大，67%精度分别提高了43%和17%。

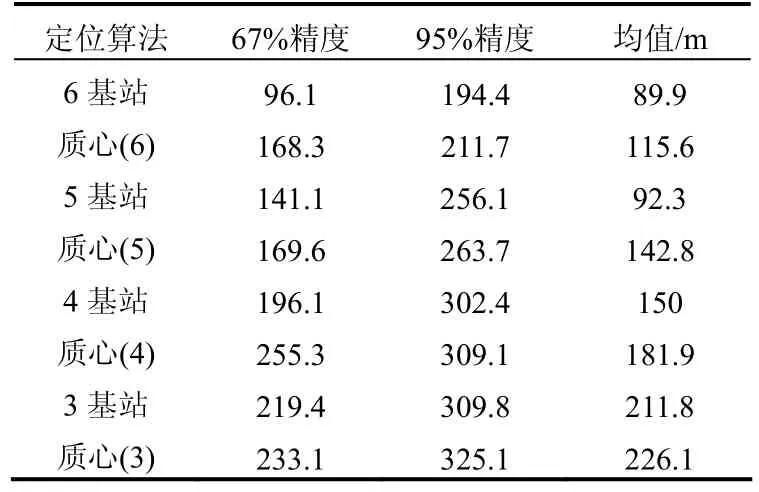
表1 改进的RSSI算法与质心算法的比较

4 结语

通过实验和统计分析，所提出的改进的基于 RSSI差值定位方法，在基站数目大于等于5时有明显优势，远优于质心定位及CI+TA定位，此方法适于处理测量报告，为网络优化 MR分析提供关键技术支持。为了继续提高定位精度，可以采用基于卡尔曼滤波的连续定位法，对用户位置进行跟踪修正。另外，该文仅给出了改进 RSSI差值定位在城区的定位精度验证，其对于郊区和农村场景的定位精度还需要进一步测试验证。

[1] 范平志,邓平,刘林.蜂窝网无线定位[M].北京:电子工业出版社,2002:18-29.

[2] LIN Dingbing,JUANG Rongtcmg,LIN Hsinpiao, et al.Mobile Location Estimation Based on Differences of Signal Attenuations for GSM Systems[C].USA:IEEE,2003:77-80.

[3] CHAN Y T, HO K C.A Simple and Efficient Estimator for Hyperbolic Location[J].IEEE Trans.on Signal Processing, 1994,42(08):1905-1915.

[4] FOY W H.Position Location Solutions by Taylor Series Estimation[J].Aerospace and Electronic Systems, 1976,AES-12(02):187-194.

[5] LIU B C.Distance Difference Error Correction by Least Square for Stationary Signal-Strength-Difference-Based Hyperbolic Location in Cellular Communications[J].IEEE Transactions on Vehicular Technology, 2008,57(01):227-238.

[6] 冯慧昭,张正平,秦水介.一种基于最小二乘法和 Taylor 级数展开法的协同定位算法[J].通信技术, 2009,42(02):210-212.

[7] 丁宏毅,柳其许,王巍.Chan 定位算法与 TDOA 估计精度的关系[J].通信技术, 2010,43(03):134-136.

[8] 张斌.GSM网络优化原理[M].第2版.北京:人民邮电出版社, 2010:213-251.

[9] HENRY L B.Radio Propagation for Mordern Wireless Systems [M].北京:电子工业出版社, 2002:192-209.

[10] 谢益溪.无线电波传播原理与应用[M].北京:人民邮电出版社,2008:176-182.