源于纵筋面混凝土劈裂的无腹筋板冲切模型

任 达,刘 坚,焦楚杰

（1.广州大学 土木工程学院,广州 510006;2.中南大学,土木建筑学院,长沙 410075）

混凝土板主要用于传递面上的荷载,其承载力一般可从弯曲和剪切两方面来考虑。相对于板的弯曲而言,人们对于剪切问题的认识还很不足。从上世纪初Talbot基础板试验起,板的剪切研究持续了百年。早先的研究多以试验为主,涉及的参量范围较广,包括混凝土强度、配筋率、构件尺寸、控制截面周长、轻骨料、钢纤维等等,其后还出现了借助钢板、高性能纤维增强复合材料（FRP）等对板进行抗冲切加固方面的探索[1-8],但多限于定性分析,或仅对数据作简单回归,所得公式缺乏物理意义。理论工作主要包括极限平衡法、弹塑性理论及能量原理的运用,辅之以有限元法等数值分析手段等[9-10],问题在于,剪切机理仍不完全清楚,模型假设与构件实际破坏过程、表现特征存在诸多偏离,精度有限或失之繁复。在寻求一般解析解有困难的情况下,若能着眼工程中大量存在、具有某些典型特征的板,从破坏特征出发建立更符合实际受力行为的理论模型,不仅可用于估计此类板的冲切承载力,对一般板破坏机理的研究亦有重要参考价值。

城市建筑工程对层高往往有限制,为节省空间、获取最大净空高度,常采用无梁楼盖结构形式,与基础板相比其楼板厚度往往不大、纵筋配筋量较大。对具有这种特征的板,从其实际破坏特征出发探讨抗力机制,并依据塑性极限理论建立相应的模型,最后与国内外文献报道的大量试验结果进行比较。

1 冲切破坏的机构特征

任何结构及构件在破坏时可能形成的机构分为两类：串联机构和并联机构[11]。前者各部分形如链条串联,例如轴心受拉杆件,某个截面失效即意味着整体破坏或断链;后者各部件以并联方式构成,只有全体部件都失效才导致机构发生破坏。若将塑性铰看成局部破坏,超静定框架或连续梁等当属此类。框架梁首个塑性铰形成后,由于塑性铰能够维持抵抗弯矩,结构还能进一步增荷,直到其它部位相继出现塑性铰,形成机动体系;就冲切破坏而言,外荷产生的剪力由冲切斜锥面上的剪压区混凝土、骨料咬合作用、纵筋销栓等3者共担,任一部分破坏后立即将剪力卸给其余部分,直至各部分均破坏并致整体丧失承载力,故从本质上说,冲切截锥面属并联机构。冲切锥面又有其特殊性,带有一定的串联特征,这一概念对于抗冲切构模十分重要。对于抗冲切机制,任何部分在失效软化后都会瞬即退出工作,原有负荷被迫向其余部分转移,这些部分可能在瞬间因不堪重负而发生连锁破坏,致使破坏锥从母体冲脱。因此,连锁破坏开始时的状态应视为极限状态,其荷载即为极限荷载,构建冲切强度计算模型必须以此状态为基础,将连锁破坏起始时刻的抗力视为极限承载力。

2 源于纵筋面劈裂错动冲切假说

以往的塑性分析通常假定,破坏机构沿斜截面发生相互错动,分析表明,与这种错动机构相应的破坏面上的正应力恒不为拉[12],因此传统的错动模型所描述的是剪压破坏,而不是剪拉破坏。剪压破坏的本质是剪压区的混凝土达到复合受力极限状态,根据上述连锁破坏概念,这等于认为：试件的破坏源于剪压区未裂混凝土部分的失效。然而通过对冲切破坏后截锥体的观测,发现从距柱周约2h0（h0为有效板厚）的冲切锥扩底起,向外沿纵筋平面常存在水平劈裂段ae（图1）,Guandalini等[4]亦在试验中观察到这一现象并做了细致的描述,其6块足尺系列板的截面图较为清楚的反映了上述事实。且当板的配筋率较大,板厚较小时,这种特征似更为明显。

图1 源于纵筋面混凝土劈裂的冲切模型

其原因可从混凝土构件粘结破坏机理探讨：首先,当纵向钢筋配筋量增大后,板内纵筋间距变小,这使得各相邻纵筋周围的混凝土劈裂裂缝之间相互连通所需的发展路径变短,即更易贯通,对那些处于纵筋平面内或其附近的裂缝来说尤甚;其次,当单位板宽所受的弯矩一定时,与厚板相比,薄板因有效厚度较小,用于抵抗弯矩的力臂也相应较短,板内纵筋受到的拉力会更大,使变形钢筋对周围混凝土的径向挤压作用更强,更利于径向裂缝的开展与延伸,当临界斜裂缝发展到纵筋位置时,极易与这些已有裂缝通连,因而,此时混凝土板较易沿纵筋平面发生劈裂。相对而言,基础板一般配筋率较小,有效厚度较大,加之板面作用有下部土体反力产生的横向压应力,一定程度上阻碍了劈裂的形成,上述现象较难出现。由此推测,对于配筋率较大的薄板,破坏截锥体的形成可能始于纵筋平面内混凝土的水平劈裂,并直接导致钢筋销栓失效,其负荷被迫向其余部分转移,进而触发连锁破坏。从破坏机理看,它是以纵筋销栓失效作为破坏源,而不是剪压区混凝土的开裂软化,与传统模型描述的情况不同,因此建立模型应以纵筋平面内,混凝土即将开裂而未裂时的受拉极限状态为依据。针对具有上述构造特征的板,由试验表征及机理分析,提出源于纵筋面混凝土劈裂的错动冲切模型,并作假定：1）破坏面构成——在几何上,该破坏模型假定冲切破坏面是由两段直线（斜直段与水平段,分别对应图1中oa与ae段）构成的折线以柱边为流动准线（图1点o的轨迹）回转而成的周界面;2）运动特征——以此破坏面为界,将板分成冲切破坏锥和外部刚域2部分,错动发生时,破坏锥沿与板面垂直方向相对于外部刚域产生竖向位移。

3 破坏准则

在完全塑性极限分析中,一般认为材料是刚塑性的。在岩土类材料（包括混凝土）的分析中,常采用M ohr-coulomb准则,它由2条关于σ轴对称的直线所构成,即τ=c-σtanφ （1）式中,φ为内摩角,如图2所示,c与φ有关,习惯上称为粘聚力,二者均为常数。

该准则是外凸强度理论的下限,相当于双剪统一强度理论中b为零的情形[13],没有考虑中间主应力效应,且与多数真三轴试验结果有差距,这必将对材料强度乃至结构极限荷载分析产生影响。

4 源于纵筋面劈裂的冲切上限解

由与屈服条件相关联的流动法则,屈服包络线上各点应该与实际破坏锥面母线依照固定角度φ一一对应,再结合前面的直母线假定可知,冲切锥母线斜直段oa与柱轴向的夹角亦为φ,由图2知c与φ存在以下关系：

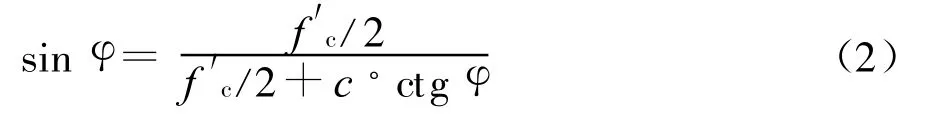
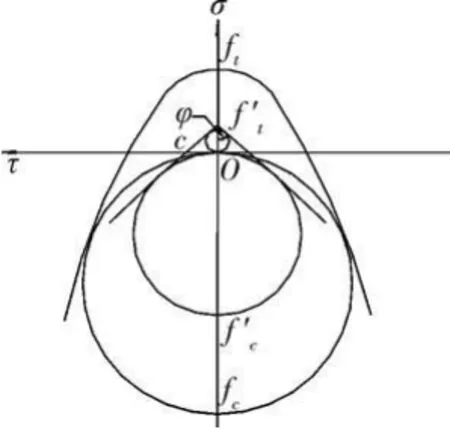
图2 材料破坏准则

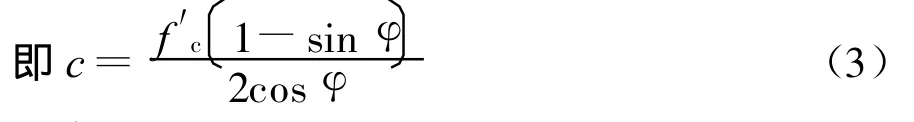
式中,f′c=νcfc,为混凝土有效抗压强度（νc为强度折减系数）。

冲切抗力上限解可通过建立虚功方程得到,但注意到破坏面上的应力分布特征,图3（a）中斜截面上的应力σ、τ经变换可以等效成图3（b）中的形式,在r-z坐标系中,由正交条件并考虑到式（1）有

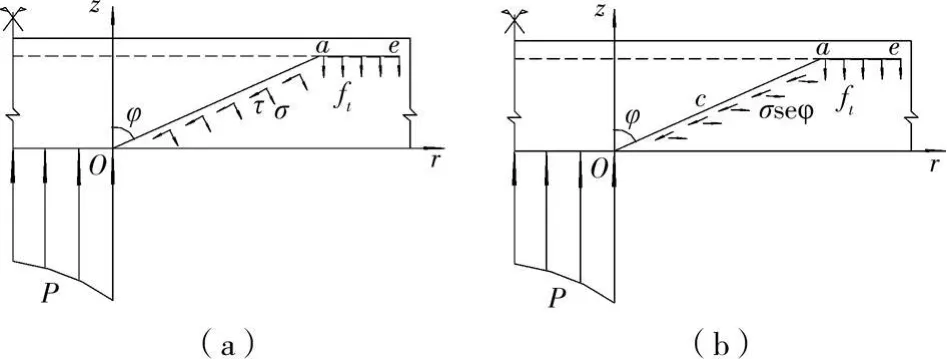
图3 破坏面上的应力等效

则图3（a）中应力σ、τ可等效为图3（b）中破坏面上的切向剪应力和径向拉应力。（此处应力系指每单位斜面积上沿箭头所指方向上的合力）

由竖向静力平衡条件建立平衡方程,可得到极限破坏荷载如下

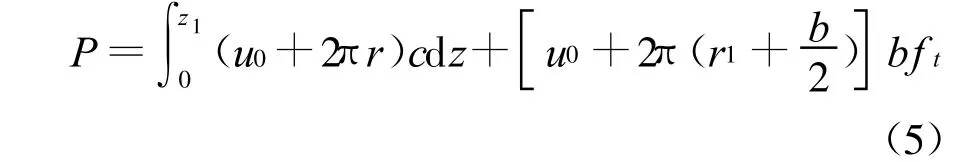
式中,u0代表柱周长,b为水平劈裂宽度,z1为构件有效厚度,r1=r（z1）,为破坏锥扩底处到柱边的距离,即图1中点a到z轴的距离。据图3,破坏锥面直母线方程设为

式中,r0=u0/2π,对于圆柱即为圆的半径,对于矩形或其它异形柱,则相当于周长为u0的该集中力域的等效半径,因此上式能适用于各种柱形。注意到secφ＞0,并令tanφ=t,上式化为

至此,极限冲切荷载P的表达式中仅剩待定参量νc与t。根据对破坏试件的观测结果,普通混凝土板的斜截面破坏锥倾角约为27°左右,即相当于t=2,故νc值可据式（8）经试验数据拟合确定。

5 理论计算值与试验值的比较

通过对国内外大量试验数据的分析,结果表明,νc对混凝土强度变化较敏感,对计算结果进行拟合得到νc～fcu关系式：νc=（fcu）-0.223,回代到式（8）可以反算出冲切荷载值,再将其与试验值比较,并以该比值为样本求得平均值为 1.072,变异系数为0.250（见表1）,可见按式（8）计算所得承载力与实测值之比的变异系数较大。

表1 理论值与试验值的比较

原因在于,源于纵筋面劈裂的错动理论模式主要是针对配筋率较大的薄板建立的,对于其它情形,如纵向配筋较弱,或板厚度较大,特别是二者同时满足的板,按该模式计算将造成理论值和试验值的较大偏离,且从计算结果看,配筋率的影响似乎更为明显,依次以ρ≥0.45,0.55,…0.85%为条件筛选出符合的试件组,结果表明：当配筋率从 0.45～0.85%以0.1%的台阶递增,理论值与试验值之比的变异系数呈递减趋势,即按该模式计算的总体精度越来越好;而当ρ超过0.85%之后,这种规律并不明显。据推测,该情形下,钢筋的间距已经足够小,此时是否发生这种沿纵筋面水平劈裂模式的冲切破坏还将取决于有效板厚、保护层厚度等因素的综合影响。为此,对满足该破坏模式要求的（ρ＞0.85%,h0≤120 mm）116块板进行了单独计算,其理论值与实测值之比的平均值（为1.017）变化不大,但变异系数为0.184,降低的幅度较大,说明用提出的源于纵筋面劈裂错动理论模式估计配筋率较大的薄板构件的极限承载力是合适的。

6 结 论

1）冲切破坏截锥面本质上属并联机构,但却带有一定的串联特征,抗冲切机制应视连锁破坏起始时刻的状态为极限状态,构建抗冲切模型必须以此状态为基础。

2）对配筋率较大的薄板,建议以纵筋销栓失效作为连锁破坏源,以纵筋平面处的混凝土将裂而未裂时的受拉极限状态为依据,建立错动冲切模型。

3）基于破坏源于纵筋面劈裂的假定,推导得到了冲切抗力上限解,并与满足模型特征的板的试验值作了比较,理论值与实测值之比的变异系数为0.184,与按所有板计算所得的变异系数0.250相比,有较大程度的降低,充分说明用上述理论模型估计配筋率较大的薄板构件的极限承载力是合理的。

[1]ASCE-ACI COMM ITTEE 326.Shear and diagonal tension,part3,slabs and footings[J].Journal of ACI,1962,59（3）：353-395.

[2]ESFAHANIM R,KIANOUSH M R,MORADIA R.Punching shear strength of interior slab-column connections strengthened with carbon fiber reinforced polymer sheets[J].Engineering Structures,2009,31（7）：1535-1542.

[3]THEODORAKOPOULOS D D,SWAMY R N.A design model for punching shear of FRP-reinforced slab-column connections[J].Cement and Concrete Composites,2008,30（6）：544-555.

[4]GUANDALIN I S,BURDET O L,M UTTONI A.Punching tests of slabs with low rein forcement ratios[J].ACIStructural Journal,2009,106（1）：87-95.

[5]LEE J H,YOON Y S,LEE S H et al.Enhancing performance of slab-column connections[J].J.Structural Engineering,2008,134（3）：448-457.

[6]SHERIF E G,EHAB E S,BRAH IM B.In fluence of rein forcement on the behavior of concrete bridge deck slabs reinforced w ith FRP Bars[J].J.Compos.for Constr.,2007,11（5）449-458.

[7]安玉杰,赵国藩,黄承逵.配筋钢纤维混凝土板抗冲切性能的试验研究[J].建筑结构学报,1994,15（2）：11-16.

AN YU-JIE,ZHAO GUO-FAN,HUANG CHENGKUI.Experimental study on punching shear resistance of SFRC slabs with steel bars[J].Journal of Building Structures,1994,15（2）：11-16.

[8]NAAM AN A E,LIKH ITRUANGSILP V,Parra-Montesinos G.Punching shear response of highperformance fiber-rein forced cementitious com posite slabs[J].ACIStruc tural Journa l,2007,104（2）：170-179.

[9]JIANG D H,SHEN JH.Strength of concrete slabs in punching shear[J].Journalof Structural Engineering,1986,112（12）：2578-2591.

[10]KINNUNEN S,NYLANDER H,TOLF.Symmetrical punching o f reinforced concrete slabs：an analy tical investigation based on non linear finite elementmodeling[J].ACIS,1988,85（3）.286-294.

[11]NOW AK A S,COLLINS K R.Reliability of structures[M].重庆：重庆大学出版社,2005.

[12]周朝阳.钢筋混凝土板和基础的冲切承载力[R].混凝土结构设计规范课题复合受力专题组研究报告（冲-1-3）,长沙：长沙铁道学院,1991.

[13]俞茂宏,ODA Y,盛谦,等.统一强度理论的发展及其在土木水利等工程中的应用和经济意义[J].建筑科学与工程学报,2005,22（1）：24-41.

YU MAO-HONG,ODA Y,SHENG QIAN,et,al.Development of unified strength theory and its app lications in civil engineering and its econom ic significance[J].Journal o f A rchitecture and Civil Engineering,2005,22（1）：24-41.

[14] REGAN P E.Symmetric punching of reinforced concrete slabs[J].M agazine of Concrete Research,1986,38（136）：18-26.

[15]任达.无腹剪混凝土板受冲、剪承载力研究[D].长沙：中南大学土木建筑学院,2002.

（编辑胡 玲）