考虑桥面板振动的桥梁结构低频噪声分析
2011-03-06布占宇黄剑源
丁 勇,布占宇,谢 旭,李 辉,黄剑源
(1.宁波大学土木工程系,宁波 315211;2.浙江大学土木工程系,杭州 310027)
考虑桥面板振动的桥梁结构低频噪声分析
丁 勇1,布占宇1,谢 旭2,李 辉1,黄剑源1
(1.宁波大学土木工程系,宁波 315211;2.浙江大学土木工程系,杭州 310027)
桥梁结构在车辆的动力作用下,将产生振动并辐射低频噪声,这种低频噪声对人体健康有很大的危害。针对这一问题,提出了一种基于桥面板振动的桥梁低频噪声预测方法,主要包括考虑桥面板振动的车桥耦合振动、桥面板辐射声波以及空气波传播分析。以一座辐射低频噪声较强的钢桥为对象,分别采用基于桥面板振动和基于梁格振动的方法计算了结构振动与噪声,并与实测值进行了对比。结果表明,基于桥面板振动的预测更为准确。在此基础上,探讨了降低桥梁低频噪声的方法,结果表明,降低桥面粗糙度可以降低桥梁低频噪声,但当达到ISO极好路面标准后,进一步降低粗糙度产生的效果不明显;对端横梁用混凝土进行加强是一种简便有效的降低桥梁低频噪声的方法。
结构振动;桥面板;有限元;表面粗糙度;低频噪声
当车辆通过桥梁时,桥梁将发生振动,并向周边 环境辐射噪声,其中频率在0-100 Hz之间的噪声称为低频噪声[1]。对于工作或生活在桥梁周边的人,如果长期暴露于这种低频噪声中,可能会产生头痛、耳鸣、失眠、腹部压迫等生理和心理反应,严重影响身体健康,这已经成为当今城市的一种环境污染。因此有必要对桥梁低频噪声进行分析,并设法降低这种噪声[1-2]。
桥梁低频噪声本质上是一种结构噪声,因此首先要分析车辆造成的桥梁振动。考虑到车辆与桥梁振动的耦合效应,需要建立车辆与桥梁相互作用的动力系统,在这个系统中,车辆往往是由车体、轮轴、轮胎和悬挂系统组成的理论模型[3],桥梁结构采用有限元模型,车辆通过桥梁的过程采用直接积分法或振型叠加法来模拟[4]。结构振动辐射的噪声可以用声能或者声压来衡量[5-7]。声能代表结构振动辐射的能量,而声压则反映了人在空间某点对于噪声的感受。结构噪声计算可以采用基于声学理论的简化方法[8],也可以采用边界元或有限元数值方法[9],其在桥梁交通振动辐射低频噪声领域的应用尚在发展中。
以往的研究曾经利用梁格模型来计算桥梁在车辆作用下的振动,并由梁格点的振动来计算桥梁声辐射[8]。这种方法计算量小,但存在2个缺点:1)梁格模型在反映桥梁结构的力学特性,特别是振动特性上误差较大;2)梁格模型得到的是梁格端点的振动位移,而声辐射是由桥面板发出的,因此梁格端点振动位移与桥面板声辐射计算存在衔接问题,由端点位移近似反映桥面板振动会带来一定的误差。
在前期研究的基础上,提出了一种基于桥面板振动的桥梁低频噪声预测方法,由桥面板的振动,利用简化的结构声辐射理论模型来计算桥梁辐射的声能和周边某点的声压;与声压计算相一致,在桥梁振动计算中,建立包含桥面板的精细化板壳桥梁模型,并考虑其与车辆的耦合作用。通过某钢梁桥辐射低频噪声的实例分析,验证了该方法的有效性。最后,利用文中提出的方法,探讨了降低桥梁低频噪声的途径。
1 桥面板振动辐射低频噪声的计算方法
1.1 桥面板声功率计算
桥梁结构的声辐射由桥面板振动产生,其中法向的振动速度分量﹒w起主要作用(图1),它可以用三角函数表示


图1 桥面板的振动速度
在大气中,桥面板振动导致的声功率可认为是桥面板上各点声强的积分[5]

其中A是桥面板面积,ρ0是大气密度;c0为大气中的声速。在当前分析中,速度幅值是频率的函数,可由速度-时间历史的傅立叶变换得到
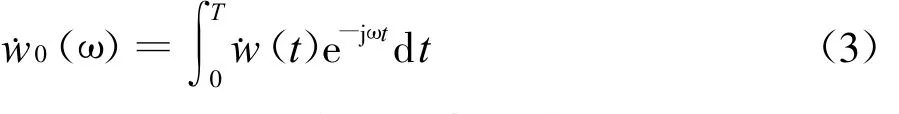
其中T为采样时间,j为虚数单位。公式(3)可由快速傅立叶变换(FFT)求解[10],代入公式(2)得到桥面板在各离散频率点的声功率,汇总后得到总声功率。声功率常常常用声功率级(单位为dB)表示

其中W0为基准声功率,W0=10-12w att。
在板壳有限元模型中,法向速度﹒w0由单元各节点的法向速度插值得到,因此某单元的声功率为

1.2 测点声压计算
在桥梁结构的上部或下部,在不计地面反射的情况下,大气中某点的声压可认为是桥面板上各点振动导致的声压之和[5]


根据公式(3),桥面板振动速度可表示为频率的函数,因此声压也是频率的函数。在当前的有限元模型中,某单元导致的声压为


其中是基准声压,=2×10-5Pa;prm s是有效声压,
2 桥面板振动的计算方法
车辆作用下的桥面板振动需要建立车桥耦合振动的系统进行分析,此外还需要考虑路面的不平整度。
2.1 车辆模型
传统的车辆理论模型导致复杂的车辆振动方程,为了克服这一缺点,用有限单元法建立车辆模型。图2所示为车辆的二维理论模型,拥有z1、z2、和 θ1共4个自由度,可得 4个动力学平衡方程[12]。为了建立该车辆的有限元模型,引入3种单元,分别为弹簧-阻尼单元[13]、集中质量单元和刚性梁单元。由此建立有限元模型如图3所示,包含9个单元7个节点,其中单元①-④为弹簧-阻尼单元,单元⑤、⑥为刚性梁单元,节点2、4、6为集中质量单元。

图2 车辆理论模型

图3 车辆有限元模型
单元组集后得到车辆动力学方程

2.2 桥梁模型
为准确反映桥梁动力特性,并与结构声辐射计算相协调,桥梁结构采用 4节点Mind lin平板壳元[11]建立有限元模型,单元组集后得到动力学方程为

其中ǜ、﹒u、u分别为节点加速度、速度和位移;M、C、K分别为质量、阻尼和刚度矩阵。结构阻尼采用瑞雷阻尼[11];F(t)为车辆的轮力荷载,考虑到车桥振动的耦合效应,F(t)由迭代得到。
2.3 路面不平整度模拟
路面不平整程度对桥梁振动响应有较大的影响,路面粗糙度r(x)可以用均值为零的平稳随机高斯过程来生成[14]

其中φk是在[0,2π]区间内随机分布的相位角,可由蒙特卡罗方法生成;x是顺桥向的坐标;n是相位角数目;其他参数定义为

其中S(Ωk)是功率谱密度(PSD)函数,Ω1和Ωu分别为最低和最高切断频率。
实际的功率谱需要基于实测数据,ISO国际标准定义了典型的功率谱[15],但是该标准要求较低,所谓的极好路面也仅相当于目前的一般路面,因此采用了图4所示A、B、C3种功率谱函数,其中B、C功率谱函数分别是A功率谱函数的20和100倍。由功率谱函数生成的路面不平整曲线样本曲线如图5所示,其中用到的参数为 Ωl=0,Ωu=6,n= 2 500。
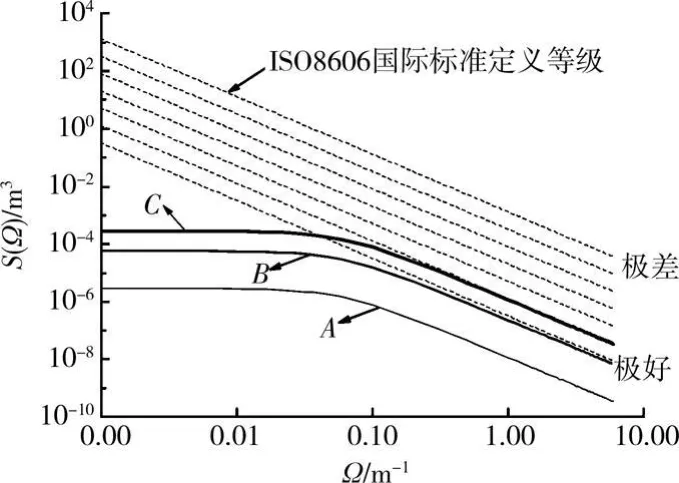
图4 路面不平整功率谱

图5 路面不平整样本曲线
2.4 车桥耦合振动的迭代算法
桥梁和车辆的动力学方程可以用直接积分法或振型迭代法求解。虽然振型迭代法能够减少计算量,但是忽略了车辆重量对桥梁振型影响,车辆较重时误差较大,因此文中采用直接积分法中的Newm ark-β法[11]计算桥梁和车辆的动力学方程。由于桥梁与车辆的振动耦合,每一个时间步桥梁和车辆的响应都是通过迭代求解的,算法如图6所示。

图6 车桥耦合振动的迭代算法
3 桥梁低频噪声实例分析
以因低频噪声遭到居民投诉的日本某简支钢箱梁桥为例,利用上述计算方法分析其结构振动与低频噪声辐射,并探讨降低低频噪声的途径。
图7为该桥的平、立面图和现场实测的照片。为了探讨计算方法对噪声预测的影响,分别建立板壳有限元模型(图8)和梁格有限元模型(图9),其中板壳模型的箱梁、U形肋、横纵梁、加劲肋等都严格按照实际结构建模,共包含 12 155个 4节点Mindlin平板壳元和10 248个节点;梁格模型按照梁格法建立,包含758个2节点梁单元和399个节点,梁单元的横截面面积、弯曲和扭转惯性矩计入桥面板的影响[16]。
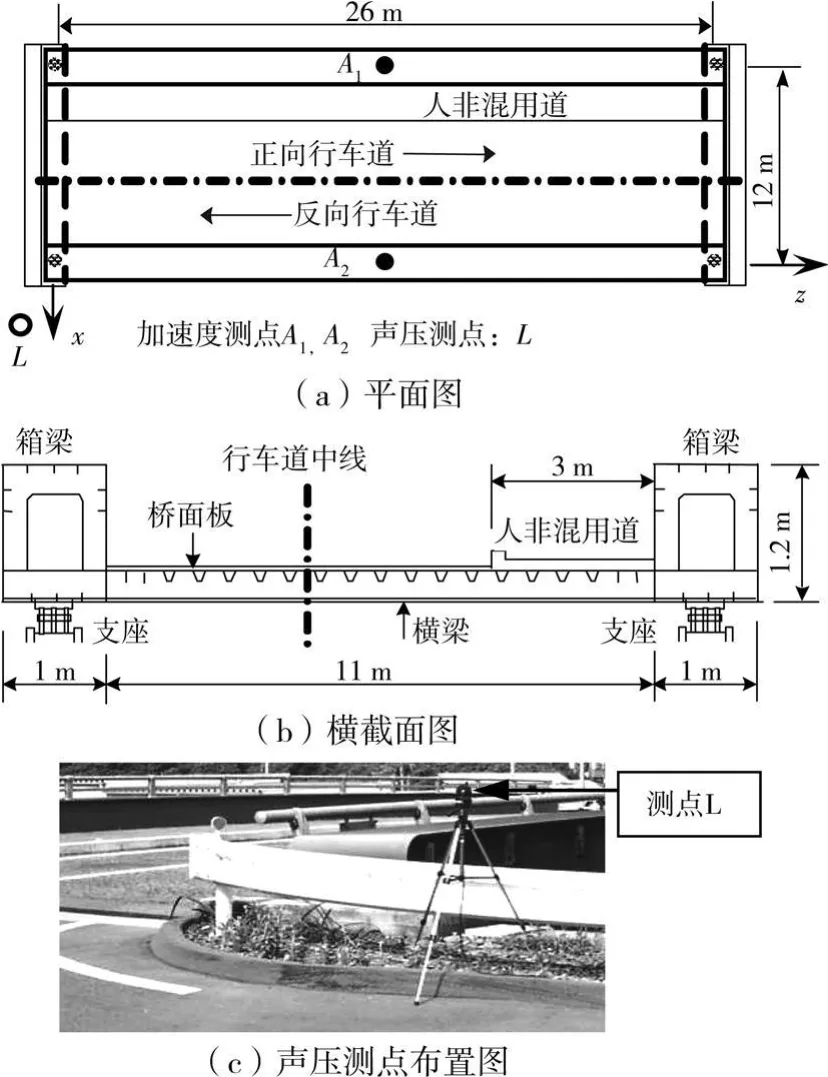
图7 简支钢箱梁桥实例

图8 板壳有限元模型

图9 梁格有限元模型
3.1 桥梁振动分析
结构振动分析是噪声计算的基础,因此本节先分析了桥梁振动的模态,然后计算车辆荷载作用下桥梁结构的振动响应。计算模型分别采用板壳和梁格两种模型,以探讨计算模型的影响。
3.1.1 振动模态分析 桥梁的自振特性反应结构的刚度指标,是动力响应分析的重要依据。分别采用板壳(图8)和梁格(图9)模型进行振动模态分析,前几阶自振频率和振型如表1和图10所示。结果表明:1)板壳模型得到的自振频率比梁格模型更接近实测值,特别是扭转振动频率(例如第2阶自振频率)方面;2)梁格模型虽然也可以反映高阶振型,但是自振频率、模态与板壳模型差别较大,例如第5、6阶自振频率差别在2 Hz以上,模态也不相同,这说明梁格模型在计算高阶频率的振动时误差较大。

表1 桥梁自振频率/Hz

图10 桥梁结构前6阶自振模态
3.1.2 车辆荷载作用下的结构振动响应 研究图2所示车辆通过图7所示桥梁时的结构振动响应,整个过程用第2节提出的计算方法来模拟,行车方向为反向行车道,车速约为40 km/h,桥面粗糙度为图5中的曲线A,车辆计算模型采用图3所示有限元模型,桥梁计算模型分别采用板壳模型(图8)和梁格模型(图9)以做比较。当桥梁采用梁格模型时,需要将轮压荷载平移到梁格的纵梁上,同时叠加扭转力偶。
图11为计算得到的桥跨中点A1、A2的加速度响应,图12为对应的实测结果。理论计算和实测都表明,车轮进桥和出桥时结构的加速度响应最大,这反映了车辆桥头冲击的影响,理论和实测的振动形态基本一致;加速度峰值对比参见表2和表3,板壳计算模型得到的加速度峰值与实测结果更加接近。以上比较表明文中算法较好地模拟出了车辆通过桥梁时结构的振动特性;而板壳模型因为准确反映了桥面板的力学特性,比梁格模型能够更准确地预测桥梁的振动。
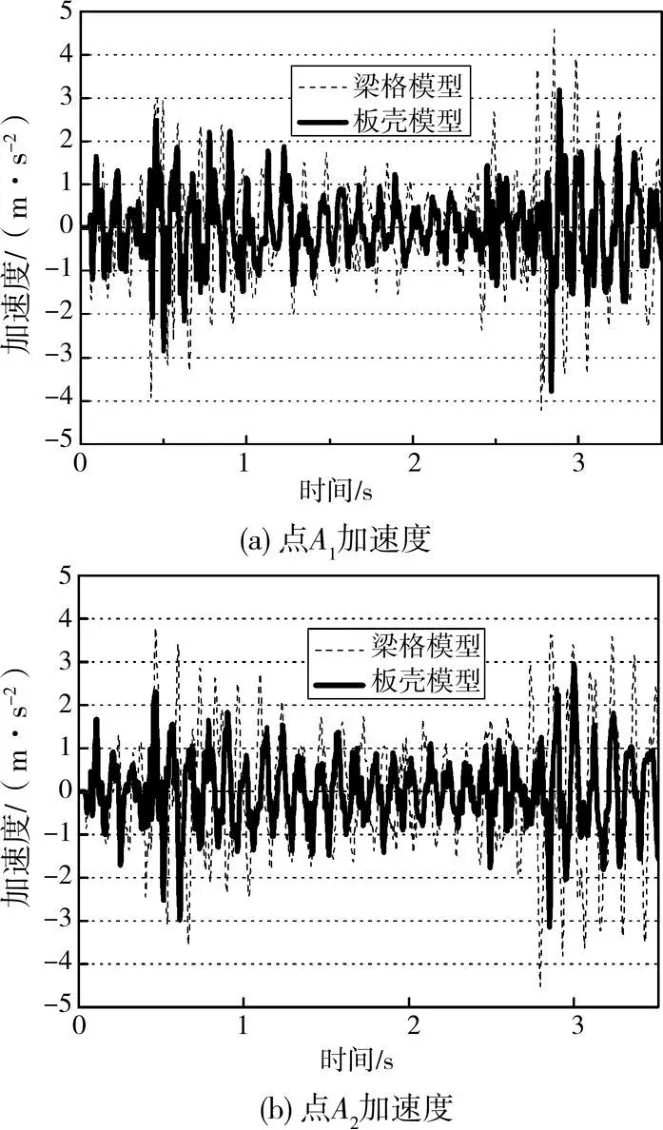
图11 计算加速度
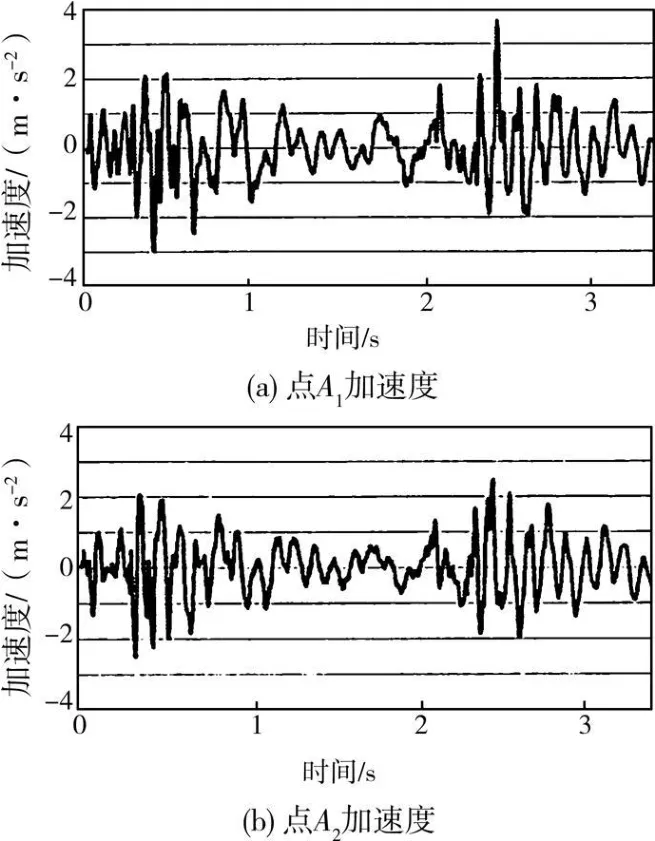
图12 实测加速度
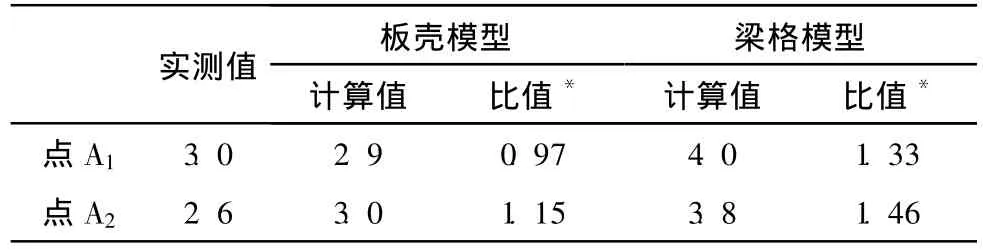
表2 车辆进桥时的加速度峰值对比/(m◦s-2)

表3 车辆出桥时的加速度峰值对比/(m◦s-2)
3.2 桥梁振动辐射低频噪声分析
基于振动分析得到桥面板振动速度,对于板壳模型,可以直接利用第1节低频噪声的计算方法,得到桥面板振动引起的声功率,以及桥梁附近某点的声压;对于梁格模型,则以梁格节点的振动速度代表该节点周围桥面板的振动速度,然后也可利用第1节的方法计算桥梁的声辐射。
与实测情况相同,车辆行驶方向分别为正向和反向行车道,车速约为30 km/h,声压测点为图7中的点L。计算时采用的车辆和桥梁模型与3.1.2节相同,由于桥面刚刚经过整治,粗糙度采用图5中曲线A,计算结果与实测结果的比较如图13所示。
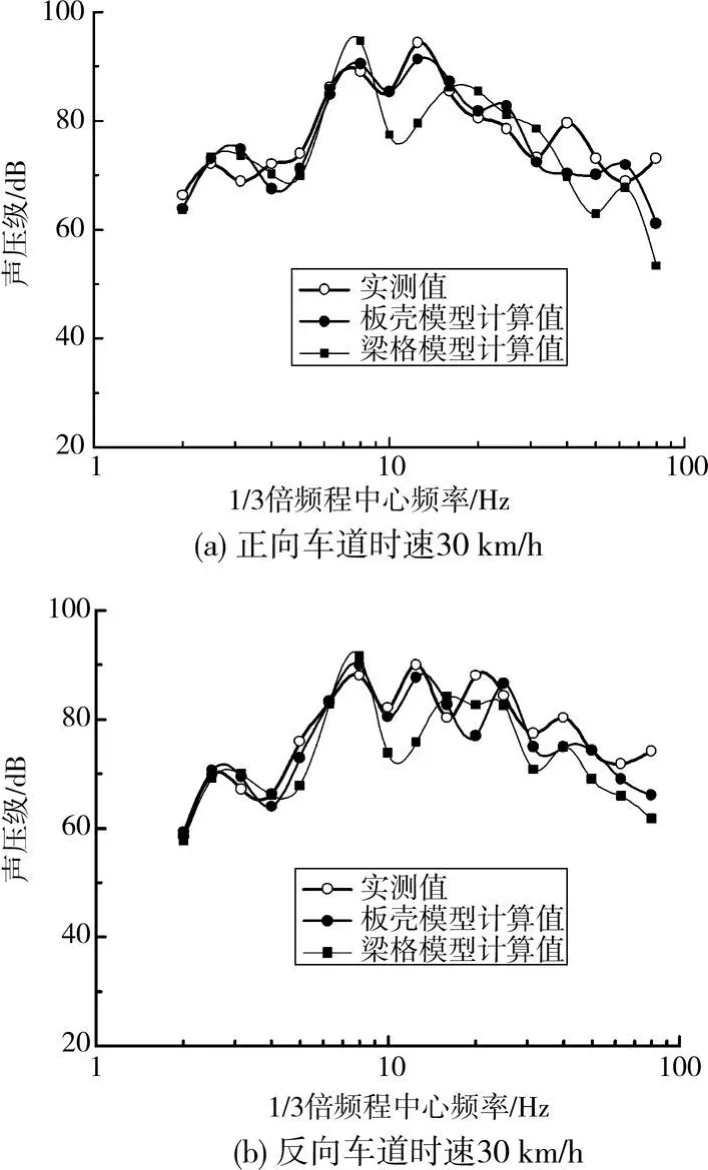
图13 桥头测点L的计算与实测声压对比
由图13可见,声压的计算与实测曲线趋势基本一致,但也存在一定的误差,误差大小可用各频带声压误差的平均值¯a来衡量

其中为第i个频带声压的误差,为计算声压,为测试声压,i为频带号,N为计算中采用的总频带数,N=17。各个频带声压误差的分散程度可用标准差σ来衡量
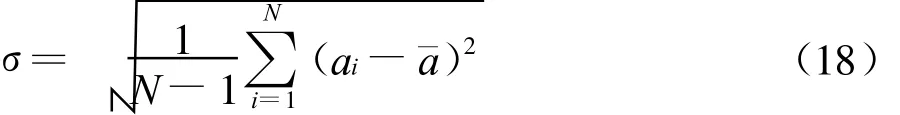
由此得到频带声压的计算误差参见表4。

表4 频带声压的计算误差/dB
由图13、表4可见,由板壳模型计算得到的频带声压曲线无论是在形态上,还是在数值上都比梁格模型更接近实测曲线(特别是8 H z以上的较高频率声压部分),误差分散程度也小,因此更适合用来估算桥梁结构低频噪声。
分析误差产生的主要原因,1)车辆、桥梁、路面粗糙度的计算模型与实际存在差异;2)严格来说,车辆通过桥梁是一个非平稳的随机过程,利用FFT方法计算桥梁振动速度的频谱会造成误差;3)实测声压包含了部分汽车和轮胎噪声,虽然这些噪声在低频噪声段要小于桥梁结构噪声,但是仍有一定影响。
桥面板振动引起的声功率参见图14。对正向车道行车情况,当频率在70 H z以下时,板壳模型计算得到的桥面板声功率与梁格模型结果接近,70 H z以上时,板壳模型的计算结果要大于梁格模型的结果。对反向车道行车情况,20 Hz以上时,板壳模型计算得到的声功率普遍大于梁格模型结果,因此对于桥面板辐射声功率的计算也有必要采用板壳模型。

图14 桥面板声功率计算值
3.3 降低桥梁低频噪声的方法
以桥面粗糙度和桥头横梁刚度为例,对降低桥梁低频噪声的方法进行算例分析,桥梁计算模型采用板壳模型,行车方向为正向车道,车速30 km/h。
3.3.1 桥面粗糙度的影响 分别采用图5中A、B、C3种路面不平整度曲线,其中A、B曲线都优于ISO国际标准中的极好路面,B、C曲线的功率谱函数分别是A曲线的20、100倍,计算车辆过桥时点L的频带声压,结果如图15所示。

图15 不同桥面粗糙渡下的桥梁结构噪声
比较路面B、C得到的声压级曲线,说明当路面粗糙度由ISO曲线中的次极好级别提高到极好级别时,桥梁辐射的低频噪声在2~60 Hz范围内都有较大降低,平均降幅4.4 dB。比较路面A、B得到的声压级曲线,说明当路面都为极好路面时,降低路面粗糙度仅能降低频率在6 Hz以下的低频噪声,平均降幅约4.4 dB。
以上比较说明,降低桥面粗糙度可以降低桥梁低频噪声;在将桥面从ISO标准中较粗糙路面提高到极好路面时降噪效果明显,进一步降低粗糙度的效果则只能降低较低频率的噪声。
3.3.2 桥头横梁刚度的影响 提高桥头横梁的刚度可以降低车辆进、出桥时的冲击效应,是一种比较方便的加固方法。桥头横梁的位置参见图8(b),其横截面参见图16(a),下翼缘厚28 mm,腹板厚16 mm,上翼缘厚12mm;该截面可用填充混凝土的方法予以加强,加强后的横截面如图16(b)。对桥梁两端的横梁都予以加强后,计算车辆过桥时测点L的频带声压,结果如图17所示。
结果表明,加强桥头横梁可以降低桥梁低频噪声,其效果在较高频率范围内更加明显,本例中2~32 H z的声压平均降低1.5 dB,32~80 H z的声压平均降低4.5 dB。作为一种简便的局部加固方法,桥头横梁填充混凝土能获得较好的降噪效果。
4 结 论
利用车桥耦合振动分析得到桥面板振动响应,根据结构噪声的理论,提出了一种基于桥面板振动的桥梁低频噪声简化分析方法,并由此探讨了降低桥梁低频噪声的途径,主要结论如下:

图16 加强前后的桥头横梁截面

图17 桥头横梁加强前后的声压级
1)板壳模型准确模拟了桥面板的力学特性,相对于梁格模型可以得到更加准确的桥梁交通振动响应,特别是扭转和高频的结构振动,因此可以为结构噪声的准确计算打下基础。
2)与实测结果的对比表明,基于桥面板振动的预测方法得到的低频噪声精度比基于梁格振动的方法有了较大提高。
3)降低桥面粗糙度可以降低桥梁低频噪声,其效果与桥面的初始情况有关。在将桥面从ISO标准中次极好路面提高到极好路面时降噪效果明显,进一步降低粗糙度则只能降低较低频率的噪声。
4)加强桥头横梁可以降低车辆对桥梁的冲击效应,有效减低桥梁低频噪声,其作用在较高频率范围内更加明显。
[1]中野有朋.实践骚音对策:骚音,低周波音,超低周波音[M].东京:日刊工业新闻社,2000.
[2]CHANPHENG T,YAMADA H,MIYATA T,et al. App lication of radiation modes to the problem of lowfrequency noise from a highw ay bridge[J].A pp lied acoustics,2004,65(2):109-123.
[3]TAN G H,BRAMELD G H,THAMBIRATNAMD P.Development of an analytical model for treating bridge-vehicle interaction[J].Engineering Structures, 1998,20(1-2):54-61.
[4]KIMC W,KAWATANI M,K IMK B.Threedimensional dynam ic analysis for bridge-vehicle interaction w ith roadway roughness[J].Computer and Structure,2005,83(19/20):1627-1645.
[5]KINSLER L E,FREY A R,COPPENS A B,et al. Fundamentals of Acoustics(4th)[M].New York:John Wiley&Sons,1999.
[6]LEE Y S,K IMS H,JANG W S.Analysis of sound radiation from the coup ling effect of vibrating noise and moving-vehiclenoise on bridges[J].Canadian Journal of Civil Engineering,2005,32(5):881-898.
[7]BEWESO G,THOMPSON D J,JONESC JC,et al. Calculation of noise from railway bridges and viaducts:Experimental validation of a rapid calculation model[J]. Journal of Sound and Vibration,2006,293(3-5):933-943.
[8]谢旭,张鹤,山下幹夫,等.桥梁振动辐射低频噪声评估方法研究[J].土木工程学报,2008,41(10):53-59.
XIE X,ZHANG H,YAMASH ITA MIK IO,et al. Theoretical analysis of low-frequency noise radiated from bridge vibrations[J].China Civil Engineering Journal,2008,41(10):53-59.
[9]MERZ S,KESSISSOGLOU N,KINNS R,et al. Minim isation of the sound power radiated by a submarine through optim isation of its resonance changer[J].Journal of Sound and Vibration,2010,329(8):980-993.
[10]BRIGHAME O.The fast Fourier transform and its applications[M].New Jersey:Prentice H all,1988.
[11]ZIENKIEWICZ O C,Tay lor R.L.The finite element method,6th edition[M].London:McGraw-Hill,2005.
[12]谢旭,朱越峰,申永刚.大跨度钢索和CFRP索斜拉桥车桥耦合振动研究[J].工程力学,2007,24(S):53-61.
XIEX,ZHU Y F,SHEN Y G.Study on vibration of long-span cab le-stayed bridge with steel and CFRP cables due to moving vehicles[J].Engineering Mechanics,2007,24(S):53-61.
[13]JU S H,LIN H T,et al.A simp le finiteelementmodel for vibration analyses induced by moving vehicles[J]. Internationa l Journal for Numerical Methods in Engineering,2006,68(12):1232-1256.
[14]AU F T K,CHENG Y S,CHEUNG Y K.Effects of random road surface roughness and long-term deflection of prestressed conc`rete girder and cable-stayed bridges on im pac t due to moving vehicles[J].Computers and Structures,2001,79(8):853-872.
[15]ISO 8608.Mechanical vibration-road surface profilesreporting ofmeasured data[S].1995.
[16]戴公连,李德建.桥梁结构空间分析设计方法与应用[M].北京:人民交通出版社,2001.
(编辑 王秀玲)
Analysis of Low-frequency Noise of Bridge Considering the Vibration of Bridge Deck
DINGYong1,BUZhan-yu1,XIEXu2,LIHui1,HUANGJian-yuan1
(1.Department of Civil Engineering,Ningbo University,N ingbo 315211,P.R.China; 2.Department of Civil Engineering,Zhejiang University,Hangzhou 310027,P.R.China)
Under thedynam ic load of vehicle,the bridgew ill vibrate and radiate low-frequency noisewhich is harm fu l to human health.A method for p redicting the low-frequency noise is proposed based on the analysisof vibration ofbridgedeck.The prediction includes theanalysis of vehicle-bridge coup ling vibration considering the bridge deck and the analysis of sound radiation and propagation in the air.By taking a bridgew ith low-frequency noise as exam ple,the vibration and sound radiation of the bridge are analyzed respectively by the currentmethod and the previousmethod based on the grillagemodel.The results show that the prediction based on the vibration of bridge deck ism ore accurate.Furthermore,themeasures to reduce the noise of bridge are explored,and the resu lts indicate that a sm oother road surface leads to lower noise.Butwhen the condition of road surface is up to the extremely good standard defined by ISO,the effect of reducing the roughness of surface is not significant.A lso,strengthening the crossbeam in the bridgehead is a sim ple and effectiveway to reduce the low-frequency noise of bridge.
Structural vibration;bridge deck;finite elem ent method;surface roughness;lowfrequency noise
U441;U491.9
A
1674-4764(2011)02-0058-07
2010-07-22
浙江省自然科学基金(Y1110548);宁波市自然科学基金(2009A 610157);宁波市交通科技项目(200912)
丁勇(1975-),男,副教授,博士后,主要从事计算结构力学、桥梁工程研究,(E-mail)dingyong@nbu.edu.cn。
