屏蔽电缆的电磁脉冲时域耦合特性研究
2011-03-06郑生全温定娥刘其凤
郑生全 温定娥 刘其凤 黄 琼 邓 峰
电磁兼容性国防科技重点实验室,湖北 武汉 430064
屏蔽电缆的电磁脉冲时域耦合特性研究
郑生全 温定娥 刘其凤 黄 琼 邓 峰
电磁兼容性国防科技重点实验室,湖北 武汉 430064
屏蔽电缆对电磁脉冲辐射场的耦合特性对电子设备、系统的电磁干扰控制和电磁脉冲防护具有重要意义。研究屏蔽电缆的双传输线模型分析方法,计算不同频段电磁脉冲辐射场激励下,两种典型的屏蔽电缆在屏蔽层两端不同接地状态时,屏蔽层和芯线上的感应电流。编织屏蔽电缆芯线上的感应电流比管状屏蔽电缆大几个数量级;由于集肤效应的影响,管状屏蔽电缆芯线上的耦合随着频率的升高而降低;编织屏蔽电缆由于编织电感和小孔电感的影响,芯线上的耦合随着频率的升高而升高。对于高灵敏的高频、微波系统,对电磁脉冲的防护时要选用管状屏蔽电缆。
屏蔽电缆;电磁脉冲;耦合电流
1 引言
电缆与天线一样,能够耦合空间电磁场的能量,在电缆表面形成高频电流,端口上产生高频电压。因此,在系统级电磁干扰控制和电磁脉冲防护设计中,要采用屏蔽电缆抑制干扰信号进入系统内部。屏蔽电缆能大大减小空间电磁场耦合到芯线上的电磁脉冲能量,从而减小高强度电磁脉冲环境对与芯线相连的器件、系统的干扰和危害[1]。但是,屏蔽电缆也不能将干扰信号完全屏蔽,主要是因为屏蔽层材料的电导率有限,不是理想的导体;另一方面,屏蔽层上常有许多孔缝,特别是通常使用的编织屏蔽电缆,在频率较高时,其屏蔽效能将明显降低。因此,准确分析和预测不同类型的屏蔽电缆在不同频段、不同负载及不同接地情况下屏蔽层的电磁脉冲耦合特性,以及芯线上的瞬态电压和电流响应特性,对电子设备和系统抗电磁脉冲设计具有非常重要的意义。
为了预测屏蔽电缆芯线上的瞬态感应电流,首先需要计算出空间电磁脉冲辐射场作用下电缆屏蔽层外表面的感应电流,再将其与屏蔽电缆的转移阻抗相乘得到芯线上单位长度的分布电压,最后,通过求解芯线、屏蔽层和负载构成的传输线系统方程,得到芯线上的耦合电流[2-3]。 因此,如何求解屏蔽层上的耦合电流、屏蔽电缆的转移阻抗以及芯线与屏蔽层构成的传输线方程,是预测屏蔽电缆芯线上感应电流的三个关键点。
2 屏蔽电缆时域耦合模型
2.1 屏蔽层耦合电流
求解屏蔽电缆屏蔽层耦合电流的时域分析方法主要有两类:磁场环路积分方法和等效电路方法[4-6]。 磁场环路积分法直接从 Maxwell方程组出发,用数值方法计算出屏蔽电缆周围的场,然后由安培定律将电缆周围的磁场进行环路积分,得到屏蔽电缆屏蔽层的耦合电流。此种方法在理论上是严格的,但对复杂的屏蔽多导体电缆系统而言,应用上存在不少困难;等效电路方法是对所要分析的电缆系统建立一组等效的传输线方程,在一定的近似条件下,将电缆内外的电场和磁场的耦合简化成电缆内外的电流和电压,通过屏蔽电缆的转移阻抗和转移导纳的耦合关系,求解电缆外部电磁场辐射时引起的内部响应,比较简单实用。
下面采用双传输线模型分析外部电磁环境与屏蔽电缆的耦合效应。图1为架设在接地平面上屏蔽电缆对电磁脉冲辐射场的耦合分析示意图,其传输线模型如图2所示。双传输线模型将屏蔽电缆与空间辐射场耦合问题分解为内外两个传输线模型。外传输线模型由电缆屏蔽层与其电流回路(大地)构成,用来求解屏蔽层的耦合电流;内传输线模型由芯线与屏蔽层内表面构成,通过屏蔽层的转移阻抗和外表皮耦合电流,计算芯线上的分布电压源,从而计算芯线上的感应电流。
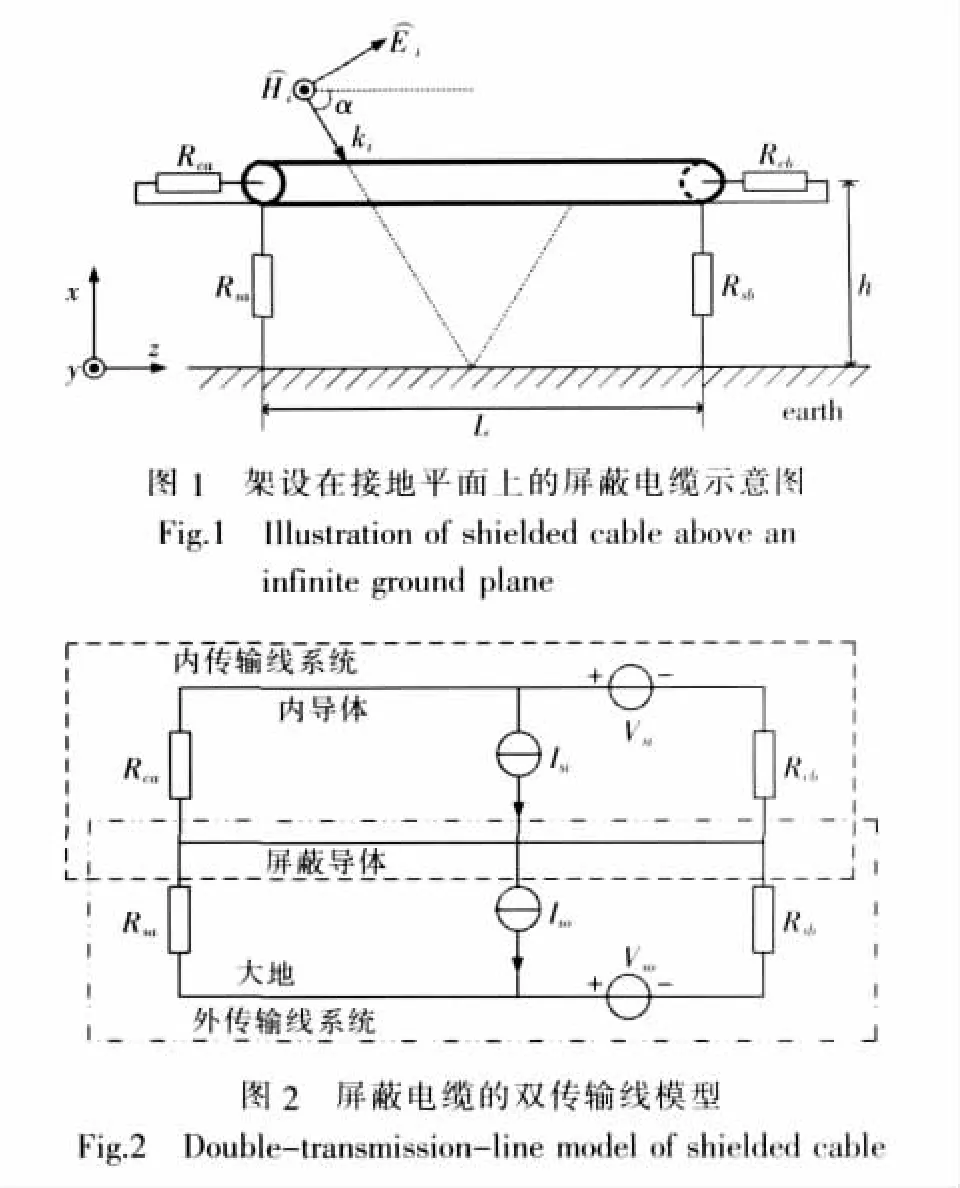
屏蔽电缆的屏蔽层与地面构成的传输线模型的时域传输线方程可用式(1)描述。

式中,R、L、C、G 分别为单位长电阻、电感、电容、电导参数矩阵;V、I分别为电压、电流列向量;VF和IF分别为外界电磁场在z处的等效分布电压源和等效分布电流源,其表达式为:
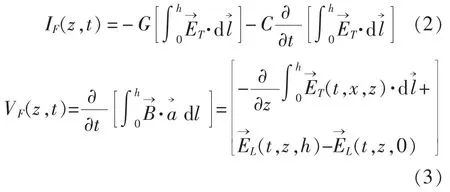
采用时域差分方法对传输线方程进行空间和时间的离散化,用中心差分近似代替偏微分。通过数值方法即可计算出空间电磁脉冲辐射场在屏蔽电缆屏蔽层上感应的等效电压源VF和等效电流源 IF的分布特性[7-9],从而求解出屏蔽电缆屏蔽层上的电压电流的时域响应。
双传输线模型法相对于频域的柱面波展开法,比较容易处理屏蔽层接地的情况。屏蔽层接地与否以及接地电阻的大小对外表皮耦合电流的影响比较大,因此对屏蔽电缆芯线的耦合影响也比较大。对于电缆两端悬空的情况(即屏蔽层两端不接地),可以采用较大的终端电阻 (Rsa=Rsb=100 MΩ);而对于屏蔽层两端接地的情况,则可以采用较小的终端电阻(Rsa=Rsb=0.01 Ω)。
2.2 屏蔽电缆的转移阻抗
内传输线系统的分布电压源与屏蔽电缆内外导体的转移阻抗密切相关。简单的屏蔽电缆结构可以采用计算公式求解转移阻抗,而比较复杂的屏蔽电缆结构,则需要通过测量来获得其转移阻抗参数。
转移阻抗将屏蔽层耦合电流与屏蔽层内纵向电场联系起来,这是因屏蔽层所用的材料总是具有有限的电导率,载流屏蔽层内的电场不为零。如果屏蔽层有缝隙(如编织型的屏蔽层),则在转移阻抗的公式中将包含互感项,此项是考虑了电磁场穿越屏蔽层上孔隙后的影响以及屏蔽层环流分量的结果。低频时,转移阻抗主要由电缆屏蔽层的扩散作用决定;高频时,电磁能量透过屏蔽层上的孔隙而耦合到电缆内部,转移阻抗主要由透射场决定。
与转移阻抗相对应的转移导纳与屏蔽层和地的电压的乘积,即为内传输线系统的分布电流源。由于转移导纳较转移阻抗小很多,因此在预测芯线上感应电流时,可以忽略。
以下给出管状屏蔽电缆和编织屏蔽电缆转移阻抗的具体计算公式。
1)管状屏蔽同轴电缆
薄管状屏蔽层的转移阻抗可以表示为:

式中,a为屏蔽层外半径;T为屏蔽层厚度;σ为屏蔽层电导率。为屏蔽层的趋肤深度。
由式(4)可以看出,转移阻抗与频率有关,是频变参数,因此在时域计算中,需要进行卷积处理。在低频时,转移阻抗简化为:

即为屏蔽层单位长度的直流电阻。
2)编织屏蔽同轴电缆
编织屏蔽同轴电缆的转移阻抗计算公式表示为:

式中,Zd是散射阻抗;Mh是小孔电感;Mb为编织电感。
对于散射阻抗,目前应用最为广泛的计算公式为:

式中,d为编织层内编织线的直径;n为编织束内的编织线数;C为编织层的编束数;θ为编织角。
对于小孔电感,Tyni的改进方法比较准确,其表达式为:
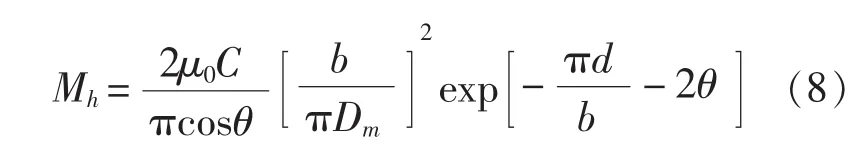
式中,Dm为编织层覆盖层的直径,表达式为:

式中,D0为绝缘层的直径;d为编织线的直径;h为两个相交叉的编织带间的距离。
对于编织电感,其表达式为:

由URM43电缆的特性参数计算可得:Mh=0.566 19 nH /m,Mb= - 2.577 6 nH /m。
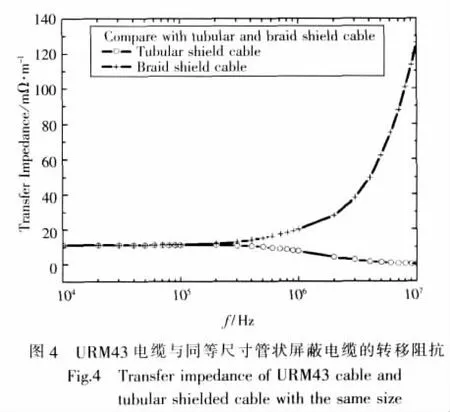
图3是编织电缆URM43的转移阻抗的计算与测量值的比较,其中测量值为文献值。

图4是与URM43同等尺寸的管状屏蔽电缆的转移阻抗。在低频时,两类屏蔽电缆的转移阻抗几乎完全一致;在高频时,编织屏蔽电缆的转移阻抗明显增加,而管状屏蔽电缆的转移阻抗逐渐减小。这是因为管状屏蔽电缆的转移阻抗只有散射电阻,没有电感项。而编织屏蔽电缆的转移阻抗既包括散射电阻,又包括电感部分。在低频段,电感部分比较小,所以转移阻抗主要以散射电阻为主,因此在低频段,两者基本一致;在高频段,由于频率的增加,导致电感部分增大,使得转移阻抗主要以电感部分为主,因此编织电缆的转移阻抗随着频率的增加而增加。而在高频段,集肤效应比较明显,随着频率的增加,集肤深度逐渐减小,因此管状电缆的转移阻抗随着频率的增大而逐渐减小。
2.3 芯线耦合响应
屏蔽层外表皮的耦合电流通过屏蔽层的转移阻抗或转移导纳在内外导体间感应出传输回路上的等效分布电压和电流源,并在电缆的芯线上引起耦合电流,对与电缆连接的设备或系统都造成干扰。
由双传输线模型可知,屏蔽层和芯线组成内传输线系统,并由等效分布电压源和电流源激励。由于转移导纳相对于转移阻抗要小得多,因此,忽略等效分布电流源的影响,而只考虑转移阻抗引起的等效分布电压源。因此,内传输线系统的传输线方程可表示为:

式中,R,L,G,C 是内传输线系统的分布参数;ZT是屏蔽电缆的转移阻抗。采用叠代方法求解方程(11),即可计算出芯线上的耦合电流和电压。
3 计算结果及分析
3.1 管状屏蔽同轴电缆
图5是外界电磁环境干扰下管状屏蔽电缆结构示意图。屏蔽电缆的长度为L=5 m,其中心距地面的高度为h=5 cm,绝缘层直径为D0=2.95 mm,屏蔽层厚度为 T =0.15 mm,芯线半径为 ri=0.45 mm;屏蔽层和芯线材料均为铜,电导率为σ=5.8×107S/m,内外导体之间的绝缘层为聚乙烯材料,其介电常数为εr=2.3。屏蔽层与芯线之间的端接电阻为Rca=Rcb=50 Ω,屏蔽层分别考虑接地与不接地两种情况。
入射电磁波为均匀平面波[10-12],其入射及极化方向如图5所示,入射角为α=45°。当t=0时,该入射波到达点(z,t)= (0,h)。
计算可得到外传输线系统的分布参数为:ls=0.823 9 μH/m 和 cs=13.504 1 pF/m,特征阻抗为Zs= 247.0 Ω; 内传输线系统的分布参数为:lc=0.237 4 μH/m 和 cc= 107.781 pF/m, 特征阻抗为Zc= 46.9 Ω。
激励源一 入射波为短波调制高斯脉冲,中心频率为 f0=15 MHz,脉冲参数分别为 τ=0.2 μs和 t0=0.8 τ= 0.16 μs,其时域波形如图 6 所示。

①屏蔽层两端不接地
图7、图8和图9分别是干扰电压电流响应。由于屏蔽层两端不接地,干扰电流比较小,因此芯线上受到的干扰也比较小。从图8和图9可以明显的看出,芯线上的干扰电流明显小于屏蔽层上的干扰电流,因此屏蔽层起到了很好的屏蔽作用。
②屏蔽层两端接地
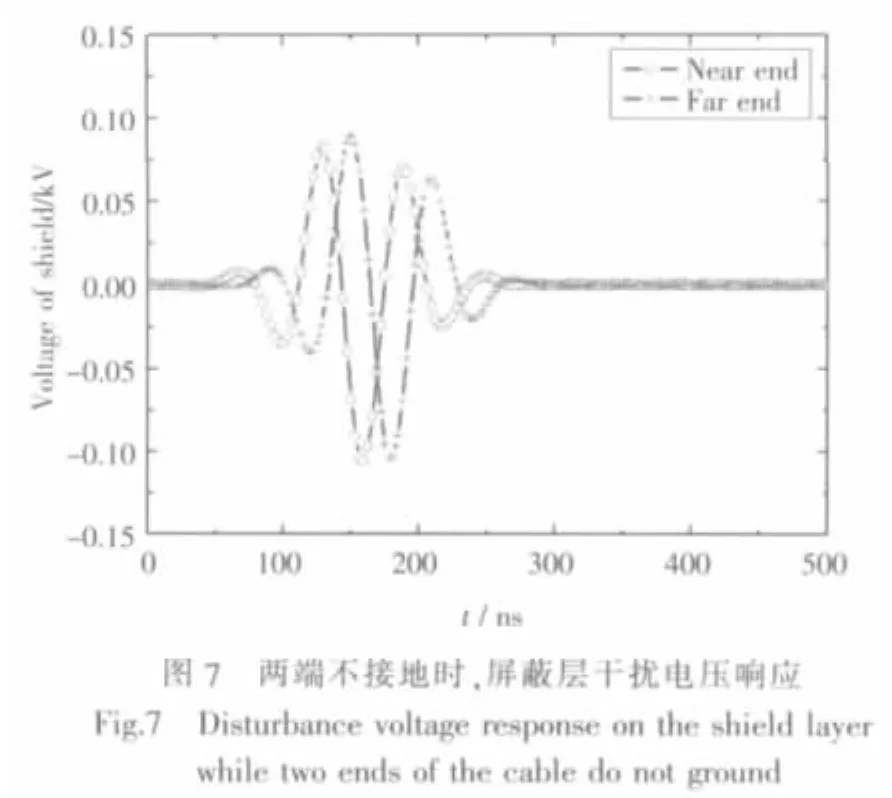

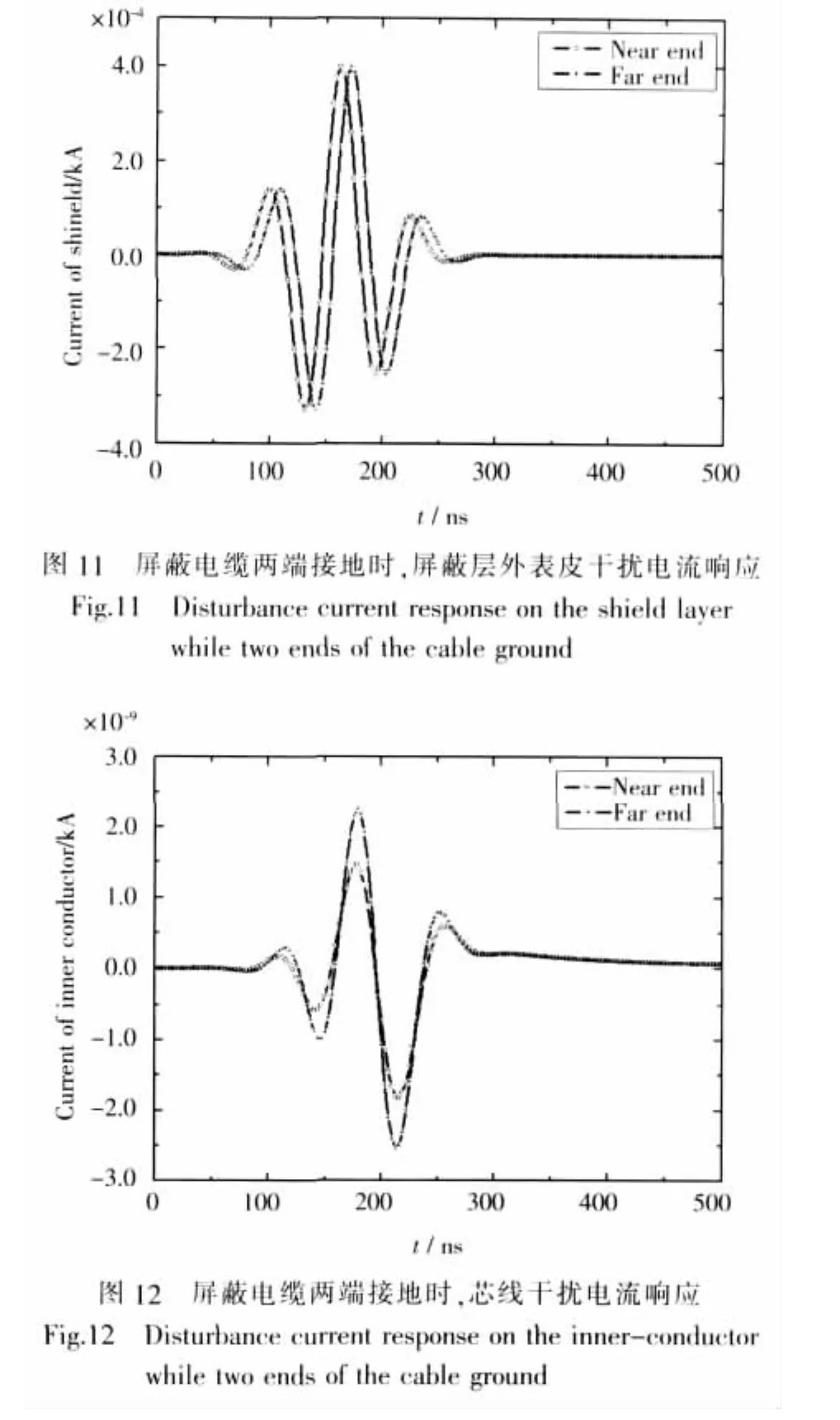
图10是屏蔽层两端接地情况下的干扰电压响应,和图7相比,屏蔽层接地情况下,干扰电压大大减小。比较图11与图8可得出,屏蔽层接地时,外表皮干扰电流明显增大,进而导致芯线的干扰电流也明显增大。因此芯线受到的干扰比屏蔽层不接地时明显增大,这一点也可以比较图12与图9看出。因此为了减少芯线受到干扰,应将屏蔽层与地面断开;但是,当屏蔽层两端不接地时,屏蔽层与地面之间的电压差也明显增大。若外界电磁场功率比较大,两端不接地时干扰电压会比较大。

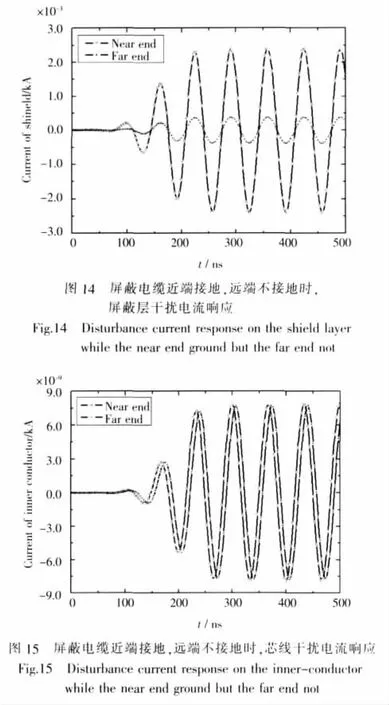
③屏蔽层近端接地,远端不接地
图13~图15分别是屏蔽层近端接地,远端不接地时,屏蔽层以及芯线的干扰电压电流响应。从图中可以看出,干扰响应存在明显的震荡效果,且震荡周期为两倍的传输线时延。比较图7、图10与图13得出:屏蔽层一端不管是与地断开还是与地良好连接,另一端的开路电压都比较大。

④屏蔽层两端接匹配电阻
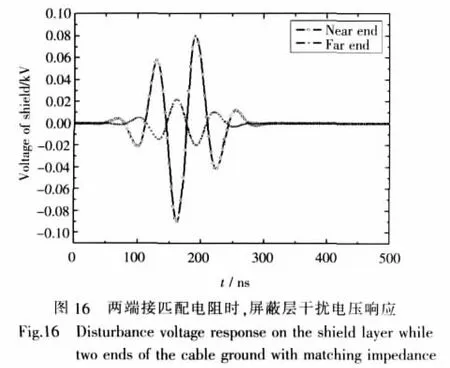

图16~图18分别是屏蔽层两端接匹配电阻时,屏蔽层以及芯线的干扰电压电流响应。比较图7、图10、图13以及图16可得出:端接匹配电阻时,干扰电压比不接地时干扰电压要小。而从图8、图11、图14以及图17可看出:端接匹配电阻时,外表皮干扰电流要比不接地情况要大,而比接地情况要小;因此端接匹配电阻时,耦合到芯线上的干扰电流同样要比不接地情况大,而比接地情况小,这可以从图9、图12、图15以及图18中明显看出。因此,屏蔽电缆的屏蔽层两端接适当的电阻,既可以相对地减小屏蔽层与地之间的电压响应,也能相对地减小芯线耦合电流的响应。因此在实际使用过程中,可以根据不同的抗干扰要求,对屏蔽电缆采取不同的接地措施。
激励源二 入射波为超短波调制高斯脉冲,中心频率为f0=150 MHz,脉冲参数分别为τ=0.02 μs和 t0= 0.08 τ=0.016 μs,其时域波形如图19所示。
图20~图22分别是屏蔽层两端接匹配电阻时,屏蔽层以及芯线的干扰电压电流响应。图17与图21比较可以看出,在两种不同频率调制高斯脉冲入射下,外表皮干扰电流响应大小差不多;而图18与图22相比较可以看出,两种情况下,芯线耦合电流响应却相差几个数量级。这是因为超短波调制高斯脉冲的频谱在 (50~250 MHz)范围内,而在10 MHz频率以上时,由于积肤效应的影响,转移阻抗逐渐减小几乎为零。

3.2 编织屏蔽同轴电缆

编织型屏蔽同轴电缆结构与图5中管状屏蔽同轴电缆结构相同,只是将管装屏蔽层改为编织屏蔽层,编织屏蔽层的参数同URM43型电缆。屏蔽层与芯线之间的端接电阻为Rca=Rcb=50 Ω,屏蔽层分别考虑接地与不接地情况。入射电磁波的情况也与图5管状屏蔽同轴电缆相同。
在计算外传输线系统时,将编织层近似看成管状结构,可以采用3.1节得到的外传输线系统的分布参数。
在图6所示的短波调制高斯脉冲入射场照射下,屏蔽层两端接匹配电阻时,屏蔽层上感应的干扰电流与管状屏蔽电缆的相同,如图17所示;芯线上的干扰电流响应如图23所示。
在图19所示的超短波调制高斯脉冲入射场照射下,屏蔽层两端接匹配电阻时,屏蔽层耦合的干扰电流与管状屏蔽电缆的相同,如图21所示;芯线上的干扰电流响应如图24所示。

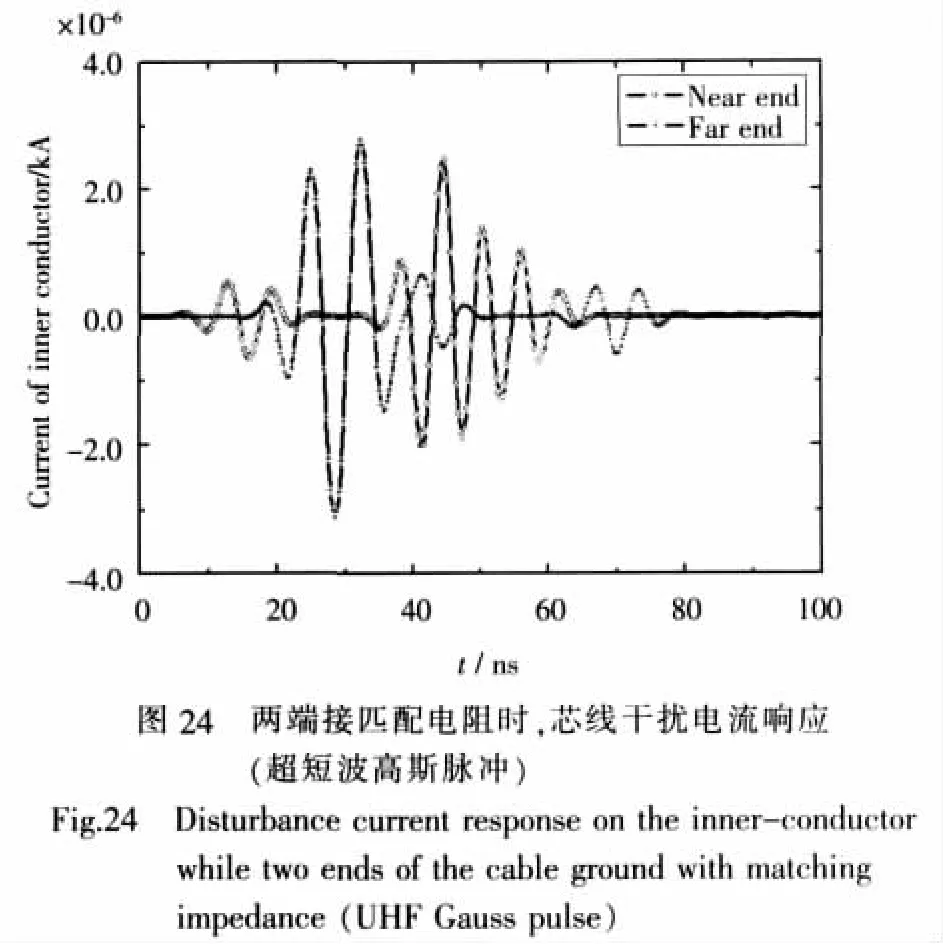
从图23和图24中明显看出,编织屏蔽同轴电缆的芯线干扰电流要明显比图18和图22中对应的管状屏蔽同轴电缆的芯线干扰电流大几个数量级。这是因为,编织电缆的转移阻抗中不仅包括频变电阻,还包括电感项,因此随着频率的增加,编织层的转移阻抗将随之增大,导致芯线的感应电流增大。
4 结束语
屏蔽电缆对电磁脉冲辐射场的耦合特性,与屏蔽电缆的长度、屏蔽层的结构、离地面的距离、屏蔽层的接地以及辐射场的频谱分量等因素有关。结构尺寸相同的管状屏蔽电缆与编织屏蔽电缆,屏蔽层与芯线的转移阻抗在低频时基本相同,而在高频时,由于编织屏蔽电缆的编织电感和小孔电感的影响,转移阻抗大大高于管状屏蔽电缆,在芯线上感应的脉冲干扰也大大增加。因此,对于高灵敏的高频、微波系统,对电磁脉冲的防护时要选用管状屏蔽电缆。在以屏蔽层作为信号回路的系统,屏蔽层的接地状态也直接影响芯线上耦合的干扰信号,此时,根据系统的特性选择合适的接地状态可以平衡屏蔽层上的感应电压和芯线上的感应电流的矛盾。
高功率电磁脉冲辐射下系统的响应特性是进行电磁安全性设计时需要考虑的重要内容。本文计算的高功率电磁脉冲激励下屏蔽电缆的屏蔽层和芯线的瞬态电压和电流响应,为分析强电磁脉冲对舰船通信网络及系统内电缆的耦合提供了方法。利用本文的预测仿真方法,得到脉冲辐射场照射时电缆上的感应电流,通过线性系统的外推方法,在电缆上注入相应的大电流,即可以模拟系统受到高场强照射时的响应特性,为电流注入替代辐射场的试验研究奠定基础。
[1]PAULC R.Introduction to Electromagnetic Compatibility[M].Second Edition.Hoboken,New Jersey:Wiley-Interscience,2006.
[2]Press J L.EMP response of a generic ground based facility[C]//IEEE International Symposium on Electromagnetic Compatibility,1990:74-79.
[3]TESCHE F M.Comparison of the transmission line and scattering models for computing the HEMP response of overhead cables [J].IEEE Trans EMC,1992,34 (2):93-99.
[4]ARI N,BLUMER W.Analytic formulation of the response of a two wire transmission line excited by a plane wave[J].IEEE Trans EMC,1988,30(4): 437-448.
[5]CLAYTON R.PAUL, Analysis of Multiconductor Transmission Lines [M].Hoboken,New Jersey:Wiley-Interscience,1994
[6]D’Amore M,Feliziani M.Induced fast transients in multiconductor shielded cables [C]//Seventh International Conference on Electromagnetic Compatibility,1990:103-108.
[7]KORDI B,LOVETRI J,BRIDEGS J E.Finite-difference analysis of dispersive transmission line within a circuit simulator [J].IEEE Trans Power Delivery,2006,21(1):234-242.
[8]FELIZIANI M,MARADEI F.Full-wave analysis of shielded cable configurations by the FDTD method [J].IEEE Trans Mngn,2002,38(2):761-764.
[9]ORLANDI A,PAUL C R.FDTD Analysis of lossy, multiconductor transmission lines terminated in arbitrary loads[J].IEEE Trans on Electromagnetic Compatibility,1996,38(3):388-389.
[10] MILLARD D P,MELIPOPULOS A P S,COKKINIDES G J.Parametric analysis of EMP induced over voltages on power lines [J].IEEE Transactions on Power Delivery,1998,3(3):1224-1231.
[11] IANOZ M,NICOARA B I C,RADASKY W A.Modeling of an EMP conducted environment [J].IEEE Trans on EMC,1996,38(3):400-413.
[12] MANSSON D,NILSSON T,THOTTAPPILLIL R.Propagation of UWB Transients in Low-Voltage Installation Power Cables[J].IEEE Trans On Electromagnetic Compatibility,2007,49(3):585-592.
The Time-Domain Coupling Characteristics of EM Pulse for Shielded Cable
Zheng Sheng-quan Wen Ding-e Liu Qi-feng Huang Qiong Deng Feng
National Key Laboratory of Science and Technology on EMC, Wuhan 430064,China
The study of the coupling characteristics of shielded cable in an EM pulse radiation field both for EMI control and EMP protection on electrical equipment and systems becomes absolutely essential.A double-transmission-line model of shielded cable was therefore investigated.The coupling current response on the shield layer and inner conductor of two typical shielded cables in different grounding states and range of frequency of EMP field were calculated.The coupling current on the inner-conductor of braid shielded cable is typically very higher in several orders than of a tubular shielded cable.The coupling current on the inner-conductor decreases along with the increase of frequency for the tubular shielded cable due to the skin effect,but increases for braid shielded cable as result of the effect of braid inductance and eyelet inductance.
shielded cable;EM pulse; coupling current
O441.4
A
1673-3185(2011)01-56-08
10.3969/j.issn.1673-3185.2011.01.011
2010-04-08
郑生全(1970-),男,硕士,高级工程师。研究方向:电磁环境与电磁防护。E-mail:zhengshengquan@hotmail.com
