三维流体动力方法计算穿浪双体船的船体响应
2011-03-05李慧敏
郑 杰 谢 伟 李慧敏
中国舰船研究设计中心,湖北武汉 430064
三维流体动力方法计算穿浪双体船的船体响应
郑 杰 谢 伟 李慧敏
中国舰船研究设计中心,湖北武汉 430064
穿浪双体船船型复杂,航速较高,要准确预报其波浪载荷比较困难,但同时对于结构设计而言又非常重要。基于线性势流理论,采用三维流体动力学方法在时域上计算了穿浪双体船的运动响应和波浪载荷,时域计算结果经过傅立叶变换,在频域上分析了其响应特征。通过与规则波中试验结果和数值计算结果进行比较分析,表明用该方法计算穿浪双体船的船体响应可以获得比较满意的结果,可应用于同类船舶的波浪载荷预报。
穿浪双体船;运动响应;波浪载荷;传递函数
1 引言
近年来,穿浪双体船因其优良的耐波性能和快速性,被越来越多地应用于高速航运市场。为保证该类船舶在高航速下船体结构的可靠性、船舶航行的舒适性以及船舶设备的正常使用,研究其在波浪中高速航行时的运动响应和波浪载荷就显得尤为重要。
用传统的切片法计算单、双体船的运动响应和波浪载荷响应已较普遍,但切片法是基于细长体和高频低速的假设来求解,而穿浪双体船高速状态下的傅氏数已达0.8以上,此时,就限制了切片法的应用[1]。
目前,用三维水动力理论求解辐射—绕射问题一般采用自由面格林函数法和简单格林函数法(Rankine源方法)[2]。Rankine源方法是在物面和自由面上都分布奇点的一种计算方法,与自由面格林函数方法相比,该方法在分布奇点计算上较为简单,并可将自由面非线性和定常势的影响考虑进去。Rankine源方法最先是在研究Kelvin波和兴波阻力时提出,之后Chapman[3]将其应用于时域有航速计算上。Nakos和Sclavounos将Rankine源方法应用到了流场定常势和非定常势的频域分析之中[4-5],并对该方法的计算稳定性进行了深入研究。Nakos和Sclavounos的研究表明[6],将该方法计入定常势的贡献后,使水动力系数特别是非对角线项的计算精度得到了显著提高,可以更为精确地预报船舶运动。近十年来,随着电子计算机技术的飞速发展,该理论方法得到了深入的研究和应用。
本文应用三维势流理论,采用简单格林函数法研究分析了某型穿浪双体船在规则波中的运动和波浪诱导载荷响应。通过与规则波模型试验结果进行比较,验证了用该方法计算高航速穿浪双体船运动和波浪载荷响应预报的可靠性,为预报其波浪载荷提供了依据。
2 规则波中船舶运动和波浪载荷理论
在规则波中,船舶运动与波浪载荷的理论计算广泛采用三维势流理论[7],其基本条件为:
·波浪及船体运动均是微幅、线性的;
·流体为无粘、无旋、不可压缩的理想流体;
·考虑绕射和辐射的影响。
2.1 三维流场的速度势求解
根据线性化假设,船舶在波浪中运动的流场速度势可以按叠加原理分为定常势和不定常势两部分:
其中,U为船舶航行速度;ΦS为定常兴波势;ΦT为不定常势。而ΦT又可分解为入射波势、辐射势和绕射势3部分:
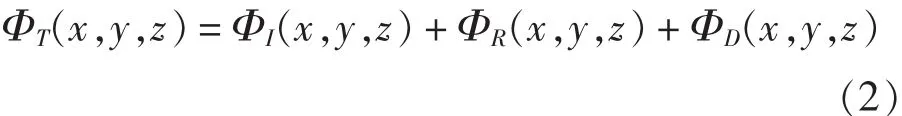
随着时间的变化,假定入射波是微幅和简谐的,因而就可以把时间因子e-iωt从速度势中分离出来:
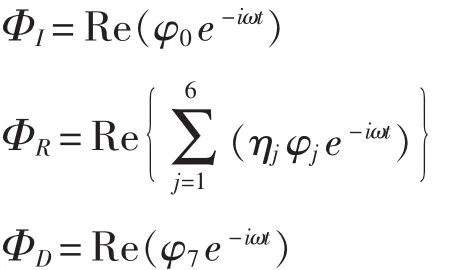

其中,入射波势φ0为已知的;ω为波浪遭遇频率;ηj是第j个运动模式的运动复幅值;φj是第j个运动模式单位幅值的振荡运动的速度势。
辐射势φj(j=1~6)和绕射势φ7可以通过求解下面的定解条件得到:

2.2 运动方程的建立
在随船平动坐标系中,利用微幅、线性化的假定条件,船舶在波浪中的耦合运动可用下面的二阶线性微分方程组表示:
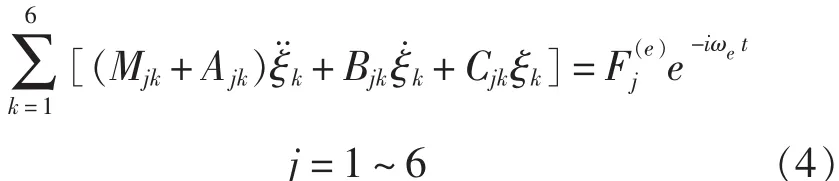
式中,Mjk为质量矩阵;Ajk为附加质量系数;Bjk为阻尼系数;Cjk为回复力系数;ξk,分别是k运动模式的位移、速度和加速度;ω为波浪遭遇频率;j和k为运动模式标号。
由于穿浪双体船的左、右片体形状相同,且相对于纵中剖面对称布置,所以船的纵向运动和横向运动之间无耦合作用。因此,可将方程组(4)解耦,得到纵向运动 (j=1,3,5)和横向运动 (j= 2,4,6)的两组独立方程。
2.3 运动响应和波浪载荷传递函数
在求得第2.1小节中流场的速度势φj(j=1~7)后,应用线性化Bernoulli方程,可得到水动压力p,积分后得到作用于船体的流体力。求得运动方程组(4)中的各水动力系数后,可进一步求得规则波中船舶运动的稳态解ζk(j=1~6)。解出规则波中的船舶运动,便可应用达朗贝尔原理计算船体各个剖面上的波浪诱导力和力矩。
规则波中,计算的重要目的是获得船舶运动和波浪载荷的频率响应函数,即传递函数。它是船舶运动与波浪载荷的响应幅值ηj和入射波幅ζ的比值,一般为复值函数,用复数极坐标形式可表示为:

3 模型试验和数值计算方法
3.1 模型试验
本文试验的船型为穿浪双体船,试验模型由玻璃钢材料制成,缩尺比为λ=18。船模的附体为带导流包的尖削水翼,水翼攻角为-2°,导流包前端位于模型的18号站处。试验采用双桨、双舵自航模试验方法。试验模型如图1所示。

实船和船模的主尺度如表1所示,规则波试验工况如表2所示。
3.2 数值计算方法
根据以上理论,本文应用以Rankine源方法为求解器的计算程序计算分析了某型穿浪双体船在规则波中的运动响应和波浪载荷频响函数。该程序在时域上计算了有航速时船舶在波浪中的运动响应和波浪载荷,时域计算结果经过Fourier变换转到频域上进行分析。
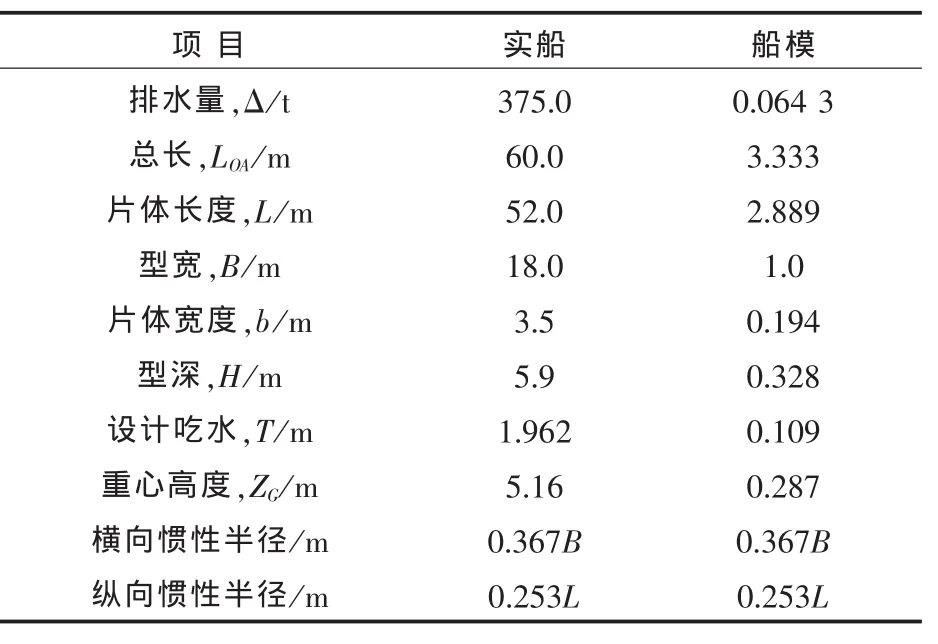
表1 实船和船模主尺度Tab.1 Principles of real ship and scale model
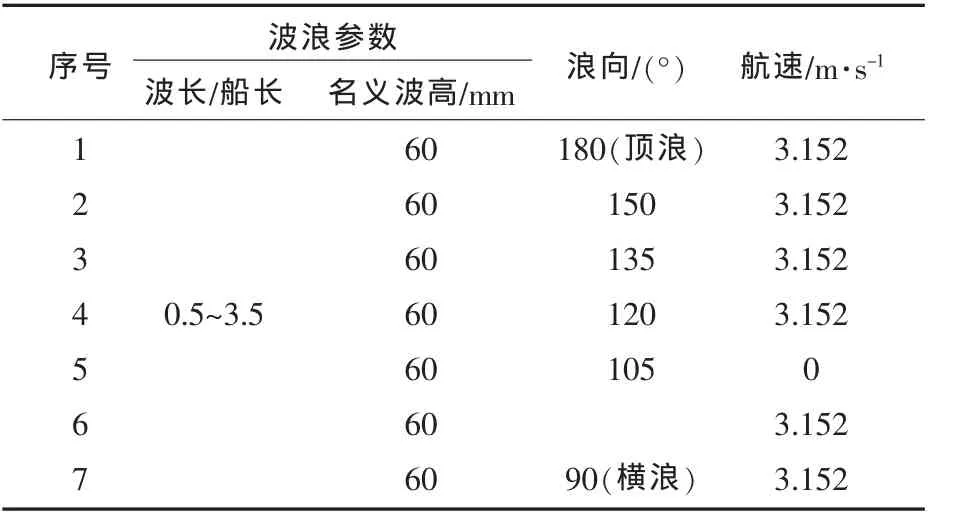
表2 规则波试验工况Tab.2 Model test conditions in regular wave
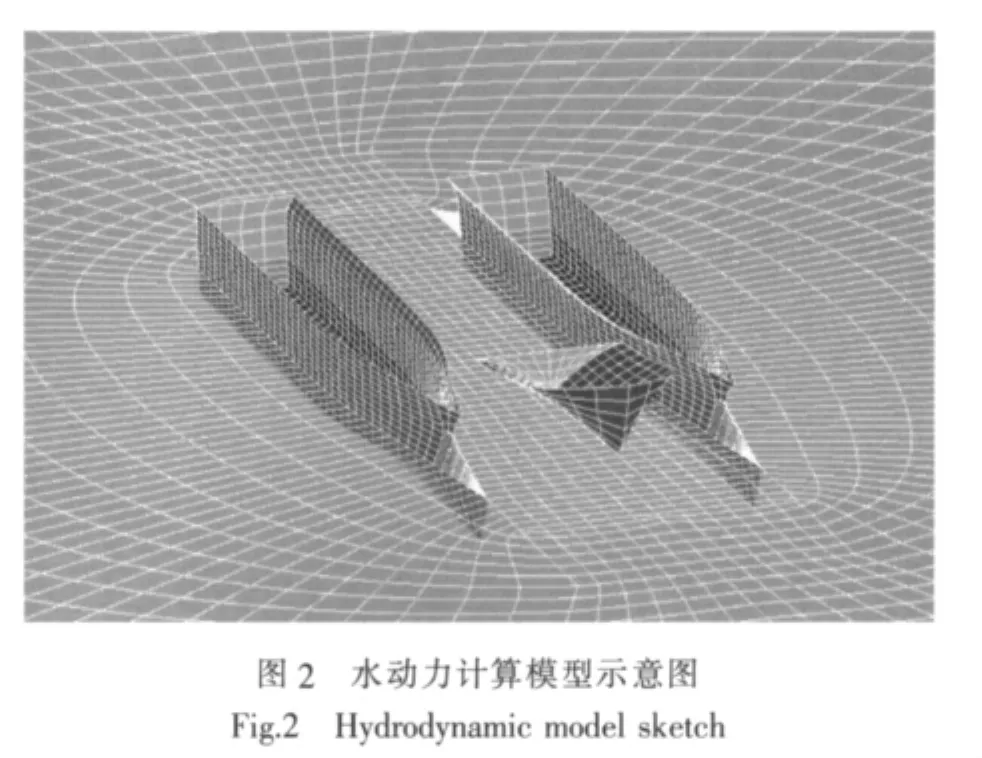
计算时,水动力模型的总重量、重心和对重心的惯性矩与实船一致,考虑到计算速度和精度,水动力计算时划分的总网格数为4 188个。其中,自由面取半径为5倍船长的圆形区域,划分网格数为3 042个,船体表面划分网格数为1 146个。水动力模型示意图如图2所示。
根据我国沿海海域的海浪统计资料[8],选择波浪周期从3~13 s、间隔为0.5 s的21个波频,浪向角从90°~180°(顶浪)、间隔为15°的7个浪向,共计147个单位波高的规则波计算船体的运动和波浪诱导载荷。
4 结果分析
为便于与该型穿浪双体船的规则波模型试验结果进行比较,本文将三维流体动力计算的运动响应与波浪载荷的结果进行了无因次化。摇荡运动的无因次化算子为1/kζ;加速度的无因次化算子为L/gζ;弯矩、扭矩的无因次化算子为1/(2ρgζBL2)。其中,k为波数(k=2π/λ);ζ为波幅;ρ为海水密度;g为重力加速度;B为片体宽;L为船长。
4.1 Fn=0.59时的运动响应和波浪诱导载荷
1)运动响应分析。
图3~8为穿浪双体船在典型浪向角下运动幅值响应的传递函数,图9和图10分别为顶浪和横浪下重心处垂向加速度的幅值响应的传递函数。
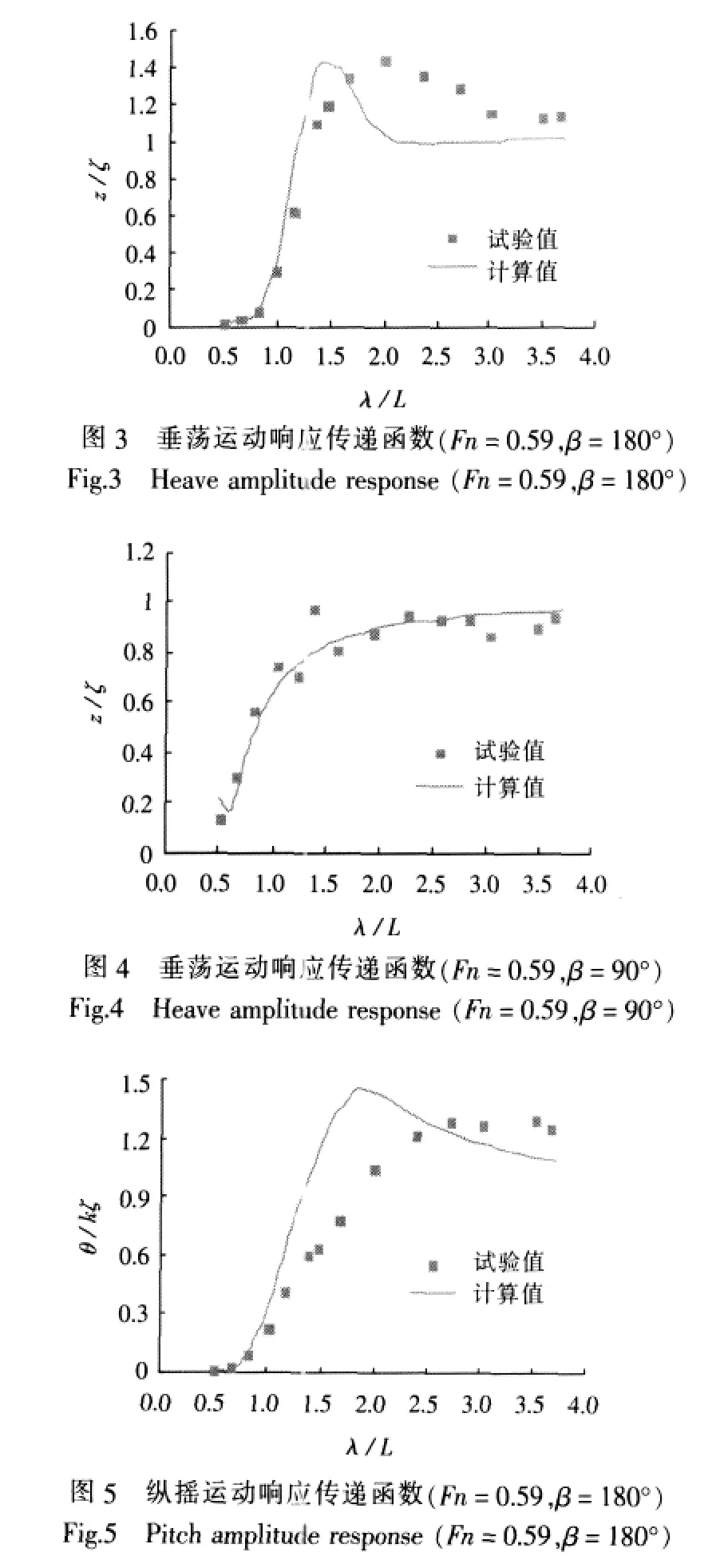
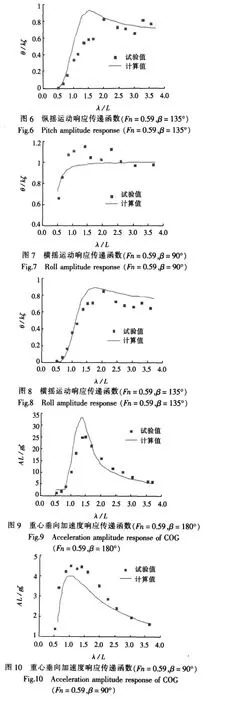
从图中可看出,在Fn=0.59的航速下,数值计算结果与试验值吻合较好。垂荡和纵摇运动的响应在顶浪时(β=180°)最大,垂荡运动的响应峰发生在波长船长比为1.5左右,纵摇运动的响应峰发生在波长船长比为1.8左右,与试验值的响应峰相比,都向短波方向有所偏移。而横浪时(β=90°),横摇运动响应最大,且在波长船长比为1.0左右时达到稳定值,这也说明穿浪双体船在波浪中有较好的横向运动响应。顶浪时,重心处的垂向加速度响应最大,响应峰发生在波长船长比为1.5左右,与垂荡运动的响应峰位置一致。横浪时,重心处的垂向加速度响应很小,最大值仅为顶浪时最大值的1/8。
2)波浪诱导载荷。
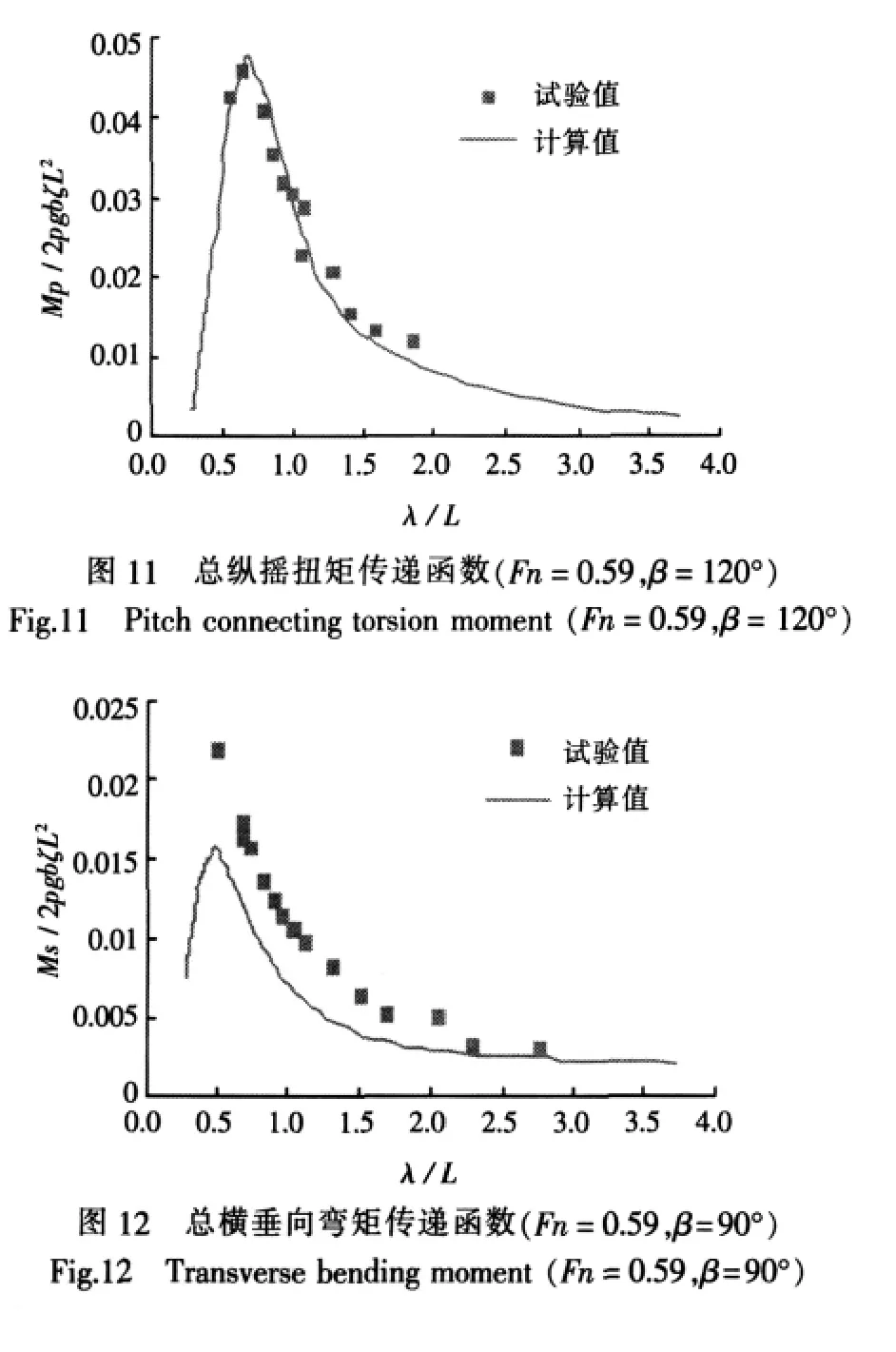
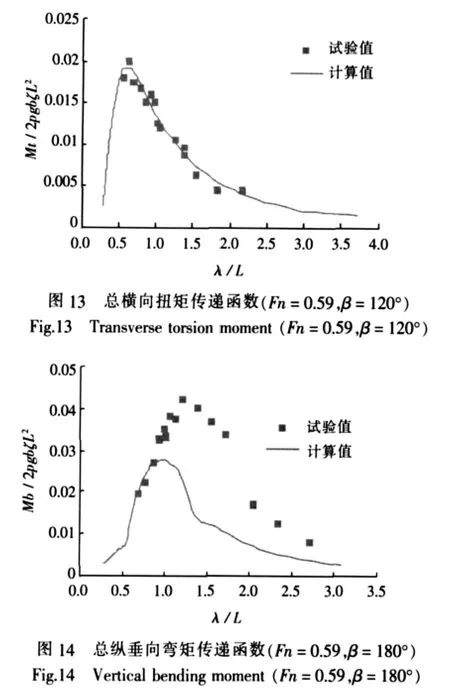
图11~14为穿浪双体船波浪诱导载荷响应最大时的幅值响应传递函数。图11和图12考查的是纵中剖面的总纵摇扭矩和总横垂向弯矩,图13和图14考查的是0.5L处横剖面的总纵垂向弯矩和总横向扭矩。
从图中可看出,在Fn=0.59的航速下,总纵摇扭矩和总横向扭矩的数值计算结果与试验结果吻合较好(由于受试验条件所限,没有获得λ/L<0.5时的试验结果),响应峰都发生在波长船长比为0.5左右。横浪时,总横垂向弯矩的响应峰发生在波长船长比为0.5左右,与试验值相比,数值计算结果偏小,但其规律与试验结果一致(λ/L<0.5时)。值得注意的是,总纵垂向弯矩在响应峰的位置和最大幅值都与试验结果差别较大,这有待于进一步的研究。
4.2 Fn=0时的运动响应和波浪诱导载荷
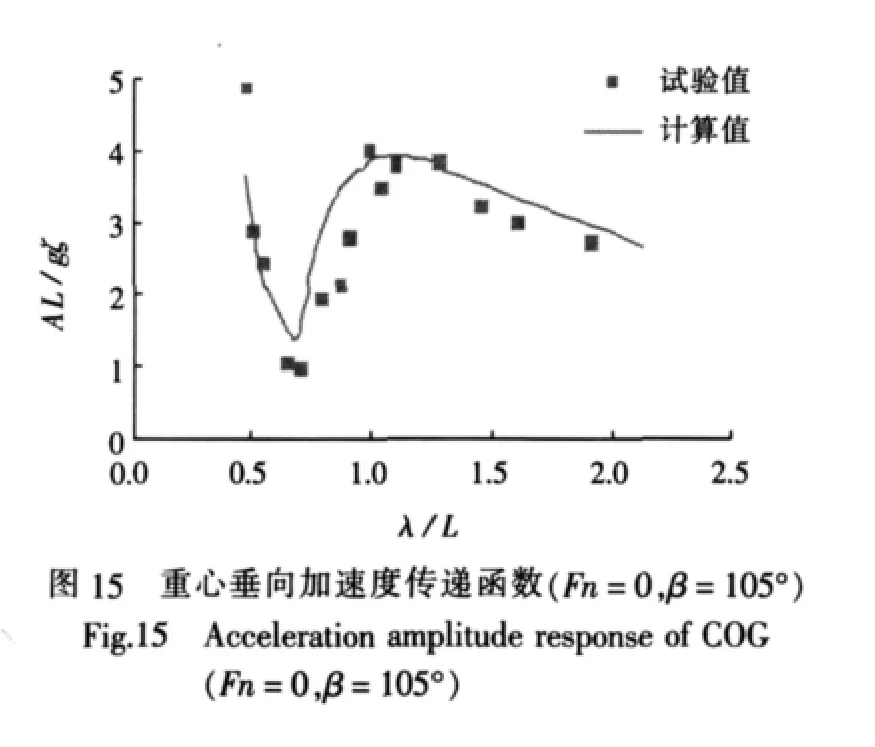
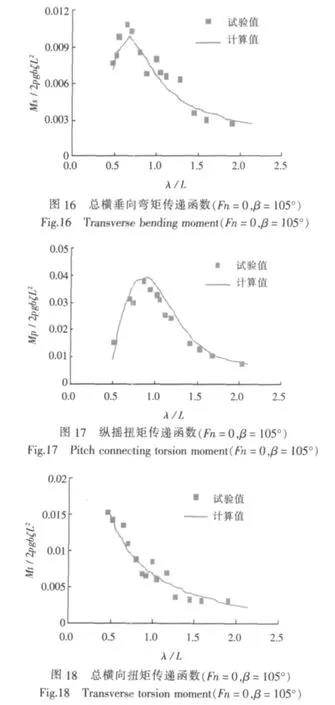
由于该试验工况下的模型试验数据不完整,所以仅给出了4个测试参数的比较。图15~18为穿浪双体船在Fn=0,浪向角β=105°时4个参数的幅值响应传递函数。
从图中可看出,在Fn=0时,重心处的垂向加速度、总横垂向弯矩、纵摇扭矩及横向扭矩的数值计算结果与试验结果均吻合较好 (由于受试验条件所限,没有获得λ/L<0.5时的试验结果)。
5 结论
通过以上分析可以知道,本文采用三维流体动力方法计算穿浪双体船在规则波中的运动响应与试验结果吻合较好。垂荡、纵摇和重心处的垂向加速度运动响应在顶浪时最大,运动响应峰值发生在波长船长比为1.5左右。数值计算结果的传递函数响应峰较试验结果均向短波方向有所偏移,产生这一现象的原因有可能是因为数值计算模型与试验模型有差别,如试验模型的折角线型及安装的首鳍对运动响应的影响。
对穿浪双体船而言,所关注的总纵摇扭矩和横向扭矩的数值计算结果与试验结果吻合较好,总横垂向弯矩的计算结果与试验结果的规律很一致,但在数值上要偏小一些。产生的原因有可能是因为横浪时,横摇运动响应的计算值比试验值略小(图7),而总横垂向弯矩又主要是由船体横摇过程中左右片体的水动力和惯性力不同所引起。
总而言之,采用三维流体动力法预报穿浪双体船的运动响应和波浪载荷可以获得比较满意的结果,其误差在工程应用的允许范围之内。在此基础上,还可应用此方法进行不规则波的运动响应和波浪载荷的长期预报,为该船型的结构优化设计提供合理的依据。
[1] 马山,宋竞正,段文洋.二维半理论和切片法的数值比较研究[J].船舶力学,2004,8(1):35-43.
[2] 秦洪德.船舶运动与波浪载荷计算的非线性方法研究[D].哈尔滨:哈尔滨工程大学,2003.
[3] CHAPMAN R B.Time-domain method for computing forces and moments acting on 3-D surface Piereing hull with forward speed,ADA 092475[R].Science Application INC,LA Jolla,CA,Sep.,1980.
[4] NAKOS D E,SCLAVOUNOS P D.On steady and unsteady ship wave patterns[J].Journal of Fluid Mechanics,1990,215:263-288.
[5] NAKOS D E,SCLAVOUNOS P D.Ship motions by a three-dimensional rankine panel method[C]//Proc.18th symp.On Naval Hydrodynamics,Ann.Arbor,MI,1990:21-40.
[6] SELAVOUNOS P D,NAKOS D E,HUANG Y.Seakeeping and wave induced loads on ship with flare by a Rankine Panel method[C]//Proceedings of the 6th International Conference on Numerical ship Hydrodynamics,Iowa City,Iowa,1993.
[7] 戴遗山.舰船在波浪中运动的频域与时域势流理论[M].北京:国防工业出版社,1998.
[8] 戴仰山,沈进威,宋竞正.船舶波浪载荷[M].北京:国防工业出版社,2007.
Motion and Wave Load Calculation of Wave-Piercing Catamaran Using 3D Hydrodynamic Method
Zheng JieXie WeiLi Hui-min
China Ship Development and Design Center,Wuhan 430064,China
Accurate prediction on the wave load of wave-piercing catamaran (WPC)is a difficult job due to its complexity and high speed performance.Based on linear potential theory,a 3D hydrodynamic method was proposed to calculate the motion response and wave loads of WPC in time domain.The numerical results were analyzed on frequency domain after fast Fourier transforming,and was then compared with the experimental results in regular waves.The result indicates that the proposed hydrodynamic method can successfully predict the motion and wave load of WPC and is applicable to the wave load prediction for similar vessel.
wave-piecing catamaran;motion response;wave load;transfer function
U661.1
A
1673-3185(2011)02-29-06
10.3969/j.issn.1673-3185.2011.02.006
2010-12-20
郑 杰(1981-),男,硕士。研究方向:船舶与海洋结构物设计制造。E-mail:zheng_jie701@163.com
谢 伟(1969-),男,研究员,博士生导师。研究方向:舰船总体优化。E-mail:xiewei@public.wh.hb.cn
