附加质量悬臂柱次随从力作用下临界力的精确解
2011-03-02薛艳霞苏振超
薛艳霞,苏振超
(五邑大学 土木建筑学院,广东 江门 529020)
附加质量悬臂柱次随从力作用下临界力的精确解
薛艳霞,苏振超
(五邑大学 土木建筑学院,广东 江门 529020)
基于相应的微分方程,推导出了次随从力作用下端部附加质量悬臂柱临界力的精确公式,讨论了次随从力参数γ和与集中质量相关的参数η对临界力参数crλ的影响,绘制了γ和η对临界力以及临界力变化率的影响曲线,并对结果进行了分析,所得的结论与数值模拟的结论一致.
悬臂柱;随从力;次随从力;次随从力参数;静态稳定性;临界力
悬臂柱在随从力作用下的静态和动态稳定性是很多学者密切关注的课题,并在实际工程中有重要应用.由于悬臂柱在随从力作用下其欧拉意义下的临界荷载不存在[1],人们开始研究次随从力作用下的悬臂柱临界力问题,如B.N.Rao等[2-5]分别对等截面和变截面悬臂柱在次随从力作用下的静态稳定性进行了分析,薛艳霞等[6]用数值方法研究了端部附加质量对次随从力作用下悬臂柱临界力的影响,本文在此基础上对端部附加集中质量的等截面悬臂柱在次随从力作用下的稳定性进行精确分析,并分别针对集中质量和次随从力对等截面悬臂柱临界力以及临界力变化率的影响进行讨论.
1 系统的微分方程
按照文献[6]中的符号和梁的Bernoulli-Euler理论,可得系统的微分方程:
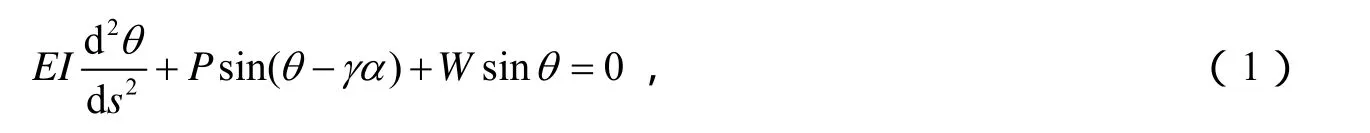
并具有边界条件:
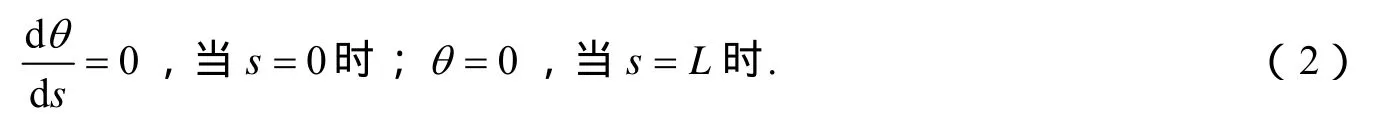
引入ξ=s/ L,则由式(l~2)可得:
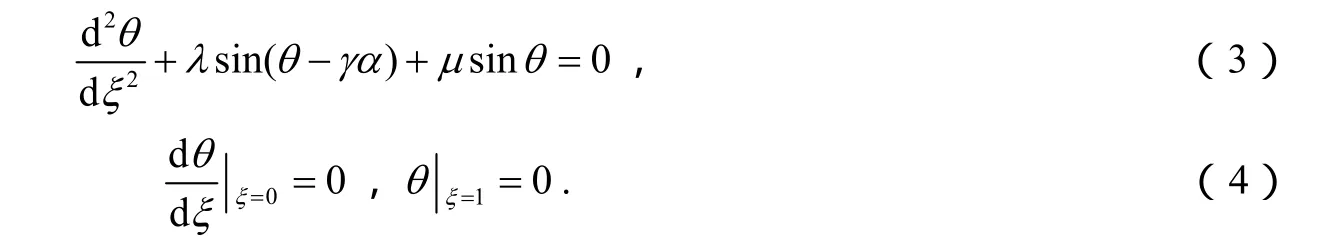
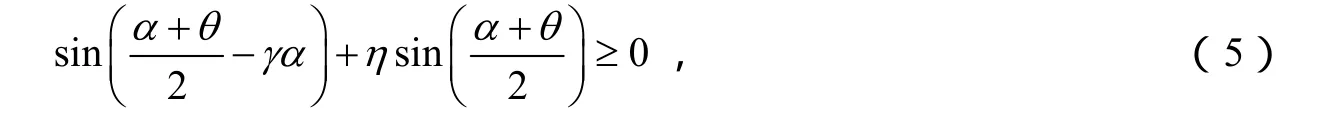
并且当θ=0时,有静力稳定平衡的条件如下:

对于η=1时有γ≤1.
从上述结果可知,如果考虑端部附加质量的重力影响,η可以大于0.5,甚至在W=P时,可以等于1.这在以后的讨论中可以看到.
2 临界力的精确解

由方程(7)可得:

令

则由式(8)可得:
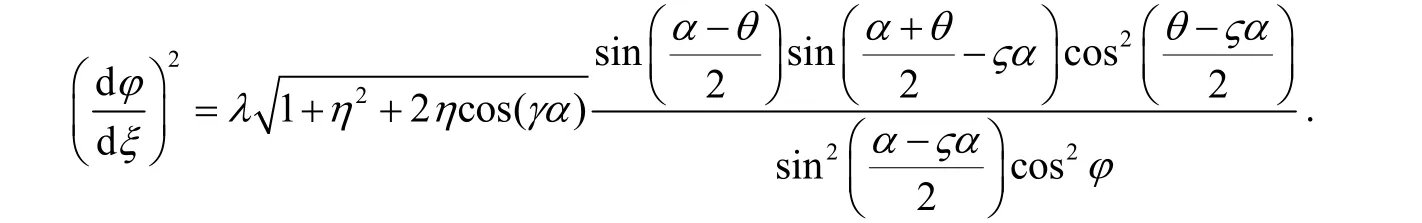
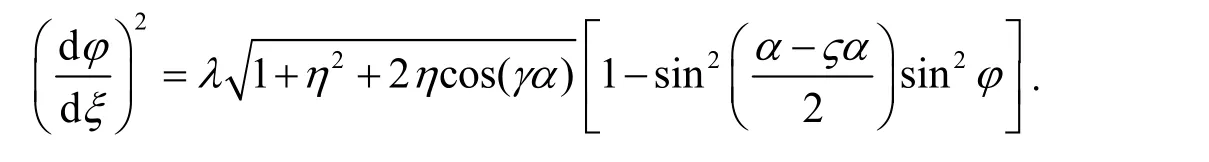
故:

边界条件可以利用式(4)和式(9)得到:

由式(10~12)可得:
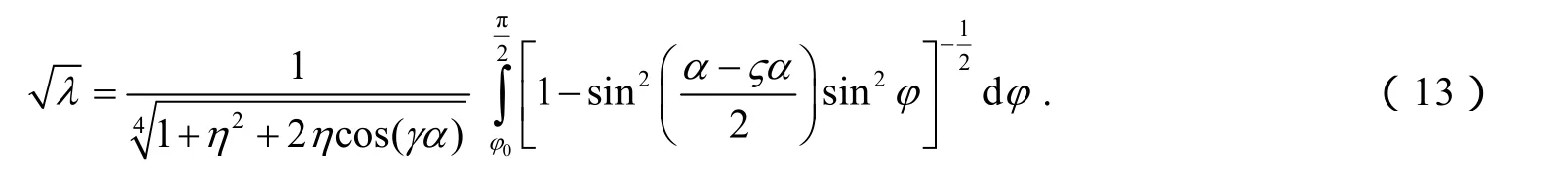
在方程(13)中,a→0时,则有 λ= λcr, λcr为线性临界力(临界荷载)参数,

所以crλ可表示为:
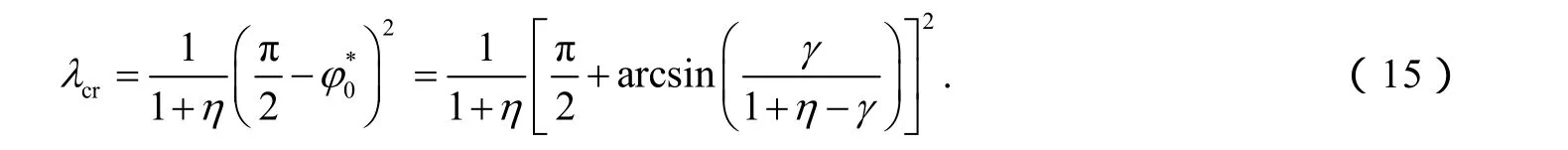
对于给定的次随从力参数γ和参数η,临界力参数crλ可以通过式(15)求解,但在计算过程中需要保证式(6)成立.式(15)中,当参数η=0时,所得到的结论就是文献[2]中的结果.
3 讨论
为了讨论次随从力参数γ和参数η对 λcr(或临界力)的影响,图1画出了当η分别取0、0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9、1.0时,λcr与次随从力参数γ的11条关系曲线.由图1可见,当η= 0时,次随从力参数γ的变化范围最小,为0~0.5,并且当η=0.5时, λcr(或临界力)取到最大值,这与周知的结论刚好吻合.当次随从力参数γ增加时,crλ(或临界力)的大小也随之增加,特别是在γ较大时,crλ(或临界力)会随着次随从力参数γ的增加而显著增加,并且随着η的增加,次随从力参数γ的变化范围逐步增加,当η=1.0时,次随从力参数γ的变化范围最大,为0~1.0,这与本文第一节的结论以及文献[6]中数值模拟求解的结果完全吻合.
当次随从力参数γ分别取0、0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9、1.0时,crλ(或临界力)与η的关系曲线见图2.从图2可以看出,当γ取0时,随着η的增加,附加质量的重力逐步增加,crλ逐步减小.事实上,这种情况演变为欧拉意义下的压杆稳定问题,由于附加质量的重力增加,荷载P对应的数值减小,所以 λcr(或临界力)也随之减小.当γ大于0时,则随着参数η的增加, λcr(或临界力)的取值逐步减小,特别是在γ较大而η较小时, λcr(或临界力)随着参数η的增加而急剧减小.同时,还可以看出,当0 ≤ γ ≤ 0.5时,η的值可以取遍0到1之间的任何值;而当γ=1时,则在η<1的范围内不能维持静态平衡,η=1这点例外.

图1 次随从力参数γ对 λcr的影响(η =0 ~1.0)

图2 η对 λcr的影响(γ =0 ~1.0)
为了进一步考察次随从力参数γ和参数η的变化对crλ(或临界力)变化的影响,分别将式(15)对γ和η求导可得:

根据式(16)、(17),考察参数γ、η的变化对临界力参数crλ的影响曲线,具体见图3~6.
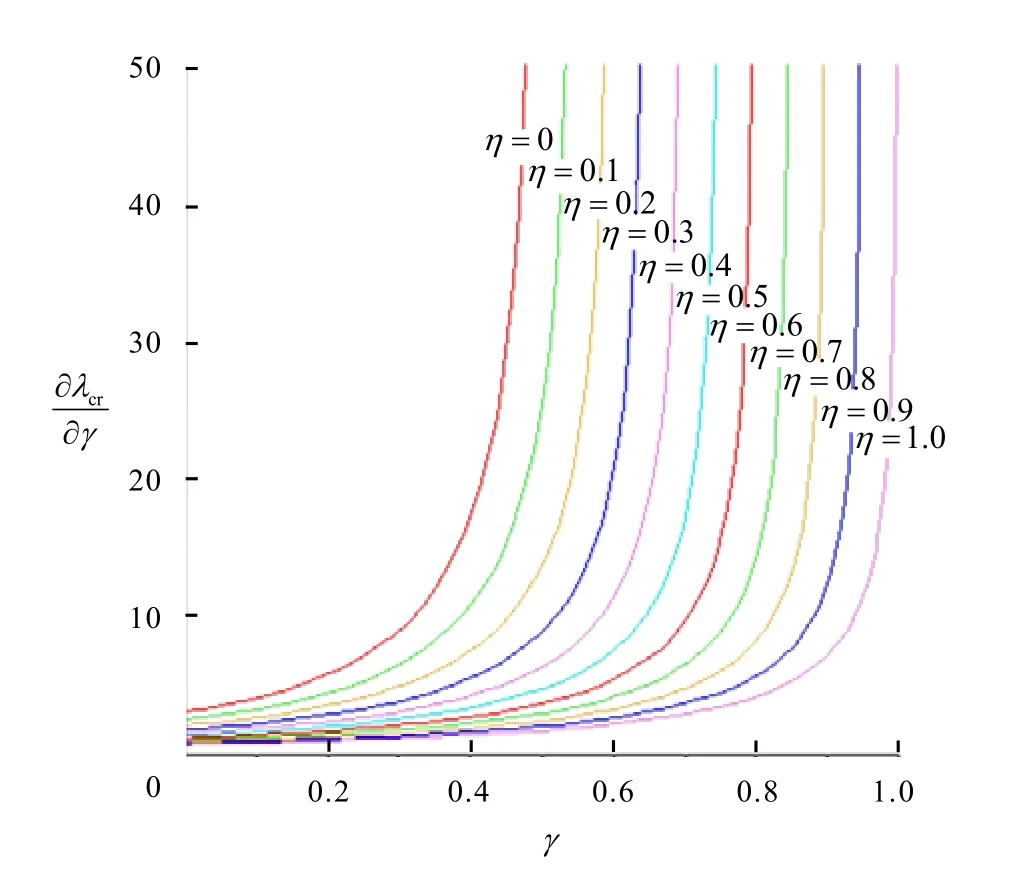
图3 γ与∂λcr/∂γ的关系
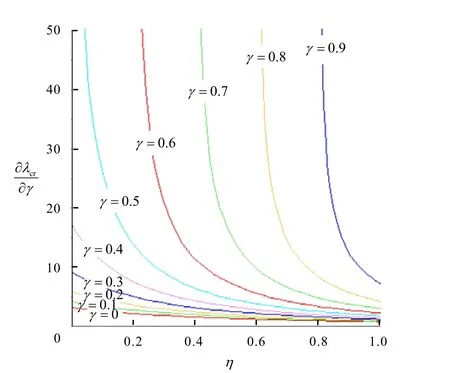
图4 η与∂λcr/∂γ的关系

图5 γ与∂λcr/∂η的关系
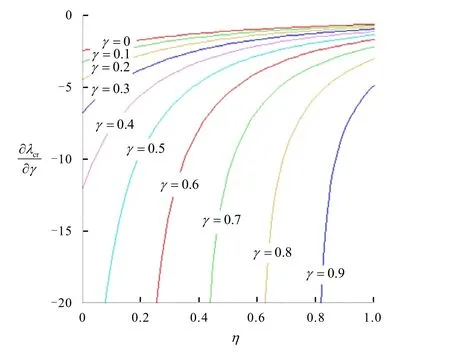
图6 η与∂λcr/∂η的关系
从图3~6可以看出,各个参数对于临界力参数λcr变化的影响与图1、图2以及文献[6]中图2的曲线变化相一致.
4 结论
本文主要讨论了端部附加集中质量时悬臂柱在次随从力作用下的稳定性,根据系统的微分方程及边界条件,通过运算得到了系统的临界力参数crλ与次随从力参数γ和与集中质量相关的参数η的精确关系式,针对参数不同的取值,绘制了相应的关系曲线,所得的结果与文献[6]中数值计算的结果相互印证,特殊情况下(η=0)的结论也文献[2]中的结果一致,并推广了该文献中的公式.
[1]REBIERE J P.Non-linear static analysis of a bar under a pure follower force[J].Journal of Sound and Vibration, 1978,60(3):459-460.
[2]RAO B N,RAO V G.Applicability of the static or dynamic criterion for the stability of a cantilever column under a tip-concentrated subtangential follower force[J].Journal of Sound and Vibration,1987,120(l):197-200.
[3]RAO B N,RAO G V.Applicability of static or dynamic criterion for the stability of a non-uniform cantilever column subjected to a tip-concentrated subtangential follower force[J].Journal of Sound and Vibration,1988, 122(1):188-191.
[4]RAO B N,RAO G V.Post-critical behaviour of Euler and Beck columns resting on an elastic foundation[J]. Journal of Sound and Vibration,2004,276:1150-1158.
[5]RAO B N,RAO G V.Stability of tapered cantilever columns with an elastic foundation subjected to a concentrated follower force at the free end[J].Journal of Sound and Vibration,1982,81(l):147-151.
[6]薛艳霞,苏振超,端部附加质量对次随从力作用下悬臂柱临界力的影响[J].五邑大学学报:自然科学版,2011,25(2):69-72.
Exact Solution of Critical Force of a Cantilever Column with Tip Mass Subjected to a Subtangential Follower Force
XUE Yan-xia,SU Zhen-chao
(School of Civil Engineering&Architecture,Wuyi University,Jiangmen 529020,China)
The stability of a cantilever column with tip mass subjected to a subtangential follower force was discussed for investigating the effects of these factors on the critical force.Based on the differential equation of the system,the exact formula for the critical force of a cantilever column with tip mass subjected to a follower force was derived.The effects of the parameters related to a subtangential follower force and the tip-mass on the critical force were analyzed,the relation curves of the subtangential follower force parameter and the tip-mass parameter on the critical force and the rate of its change were plotted,and the results were discussed.
cantilever column;follower force;subtangential follower force;subtangential follower force parameter;static stability;critical force
?
TB124
A
1006-7302(2011)03-0040-05
2011-03-21
薛艳霞(1968—),女,河南民权人,讲师,主要从事结构工程及力学的研究与教学.
