光格中二维强非局域孤子的振荡特性

王玉青，钟东洲，黄东，王天雷

（五邑大学 信息工程学院，广东 江门 529020）

光格中二维强非局域孤子的振荡特性

王玉青，钟东洲，黄东，王天雷

（五邑大学 信息工程学院，广东 江门 529020）

利用有效粒子法，研究了折射率有纵向和横向调制的强非局域非线性介质中椭圆高斯光束的传输特性，得到了光束中心在不同调制情况下的演化规律.解析和数值结果表明：无纵向调制时，介质二相等（不相等）的横向调制频率(kx,ky)将使初始偏离二坐标轴较小的光束中心演化具有相同（不相同）的振荡周期；当光束中心初始偏离某一坐标轴较远，若 kx≠ky，光束中心将分别独立地做等幅周期振荡，但若 kx=ky，光束中心周期振荡，且其振荡幅度将沿初始偏离坐标轴较小的方向逐渐指数增长而沿初始偏离坐标轴较大的方向指数衰减；当介质有纵向调制时，若纵向调制频率kz和kx、ky之间满足特定条件，则光束中心沿该横向振荡的幅度随传输距离的增加而指数增长，之后又指数减小；若不满足该频率条件，则光束中心将按不同的频率等幅周期振荡.

非线性光学；非局域非线性薛定谔方程；有效粒子法；空间光孤子

1997年，Snyder等[1]通过对非局域响应函数进行泰勒展开，把描述光束传输的非局域非线性薛定谔方程简化为一个线性谐振子方程，得到了稳定的高斯型空间光孤子解，从此掀起了研究空间光孤子的热潮[2-15].2004年，Yaroslav.V.Kartashov等[13]发现在折射率有纵向和横向调制的克尔介质中传输的光束将发生参量放大情况；2005年，Yaroslav.V.Kartashov等[14]又研究了饱和的非线性克尔介质中二维孤子的传输特性，发现当折射率有纵向和横向调制时，不同的调制使二维孤子的中心按照不同的规律振荡；2008年，郭旗等[15]曾对光格中有初始入射角的光束的传输特性进行研究，发现存在临界入射角使得光束能自陷于光格中，若光束入射角度大于该临界入射角，则光束将具有较大的初速度以挣脱光格的限制；2010年，周骏等[11]对一维强非局域光晶格结构中空间孤子的脉动传播进行了数值研究，并对影响脉动传播的内在物理机制进行了讨论.虽然目前已对横向折射率调制的非局域非线性介质中光束的传输特性有详细研究，但如果对非局域非线性介质同时加有纵向和横向的折射率调制，且入射光束中心偏离响应函数中心的情况却没有展开研究.本文首次利用有效粒子法[16]对椭圆高斯光束在此类介质中的传输特性进行详细研究.

1 传输模型

傍轴光束在有横向和纵向调制的非局域非线性介质中的传输遵循如下薛定谔方程[6,9,12]：

其中 ψ( x, y, z)为归一化的傍轴近似光束函数，x和y是按光束初始束宽a0归一化之后的横向空间坐标，z是按瑞利距离zR归一化的纵向传输坐标， p为介质的横向调制深度，R( x, y)是实对称的非线性响应函数，且R( x, y)满足归一化条件 ∫R( x, y) dx d y=1，M( x, y) =cos(kxx) cos(kyy)和 Q( z) =1 -μcos(kzz )分别代表频率为kx、ky的横向调制和频率为kz的纵向调制为介质的纵向调制深度（μ越大，纵向上的势垒越高，反射波越强，所以为减小反射波的影响，通常纵向调制比较微弱）.

2 解析结果

2.1 无调制时光束的演化规律

已有研究[7]表明：当强非局域介质的折射率无任何调制时，光束具有稳定的椭圆高斯型解，当输入功率等于临界功率（即 P0=Pcx=Pcy）时，从束腰入射的椭圆高斯光束的衍射展宽和非线性压缩才同时达到平衡，形成稳定的椭圆高斯光孤子，而当 P0=Pcx（ 或 P0=Pcy）且 Pcx≠Pcy时，光束在x（或y）方向保持束宽不变，形成单方向孤子解.

2.2 有调制时光束的演化规律

若对介质的折射率加上横向的周期调制，当光格周期远大于光束束宽时，光束近似保持稳定的椭圆高斯型分布，而当光格周期与光束束宽可比拟时，光束所受的调制作用增强，随着传输距离的增加将偏离其初始波形.

若对介质的折射率同时加上纵向调制，则光束将具有不同的运动特征，光束中心的演化满足如下方程组[13-15]：

假设光束在强非局域介质中能保持稳定传输，则方程（1）具有椭圆高斯型试探解：

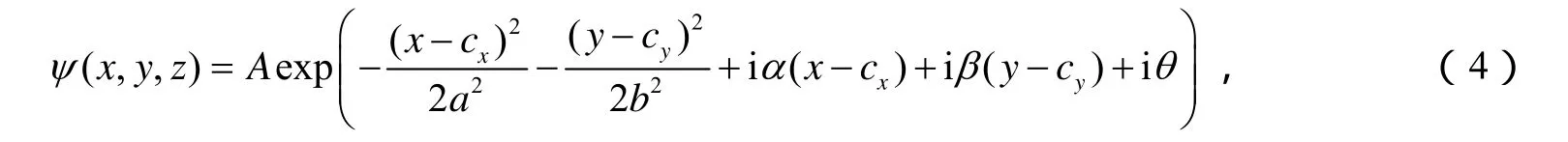
式中a、b分别为x、y方向的光束束宽，α、β分别为光束中心沿x、y方向的初速度为试探解的振幅，θ为试探解的相位.

将式（4）代入方程（1）中可得光束中心的演化规律满足如下方程组：

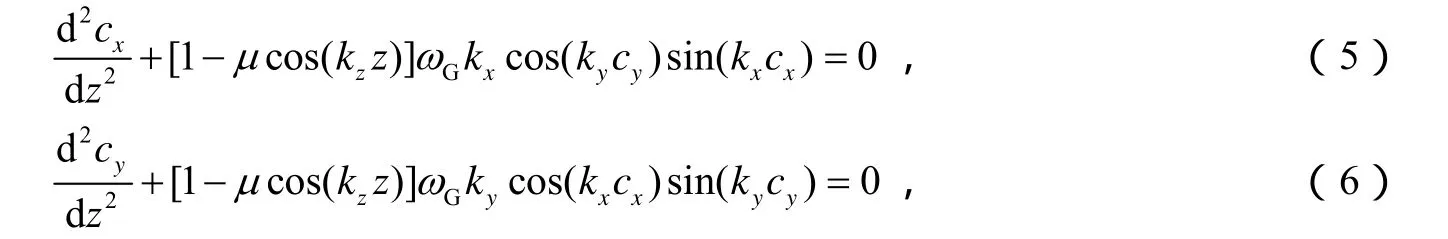
3 对解析结果的讨论

3.1 无纵向调制时光束中心的演化特征

无纵向调制时μ=0，此时若光束中心偏离x轴和y轴很小，即 cx≈0、 cy≈ 0，则光束中心将分别沿x轴和y轴发生周期振荡，由方程（5）和（6），光束中心的振荡频率分别为和由此可得光束中心的振荡频率和光格的调制深度及调制频率有关，且当 kx=ky时，光束中心具有相同的振荡周期，而当 kx≠ky时，光束中心按不同的频率周期振荡.

若μ=0但光束中心偏离x轴或y轴较大时，方程（5）和（6）不能解析求解，为研究其运动规律，对其进行数值积分.结果表明：当光束中心初始偏离x(y)轴较大而偏离y(x)轴很小时，若二横向调制频率不相等，则光束中心将保持等频率等幅度的周期振荡；若二横向调制频率相等，即 kx=ky，则光束中心在周期振荡的同时，其振荡幅度将沿y(x)方向指数增长而沿x(y)方向指数衰减，这是因为随着传输距离的增加，光束的二正交偏振方向将由于相互作用而耦合，从而产生共振.当光束中心初始偏离x轴和y轴均较大但二者相差不大时，不论横向调制频率是否相等，光束中心将按不同的频率等幅周期振荡.

3.2 有纵向调制时光束中心的演化特征

若μ≠0，则光束在传输过程中受横向和纵向的双重调制，此时光束将展现有趣的特征：当调制频率满足条件 kz≈ 2ωx（或 kz≈ 2ωy）时，光束中心沿x(y)方向的振荡幅度随传输距离的增加而指数增长，之后又指数减小；若不满足该条件，则光束中心将按不同的频率等幅周期振荡.

以下所有图中虚线（实线）均代表数值积分结果中光束中心在x(y)轴方向上的演化规律，星线（圆圈线）代表数值模拟结果中光束中心沿x(y)方向的演化规律，且满足条件 α=β= 0，a=1，b=1.2.图1给出光束中心演化轨迹的数值积分结果，其中μ=0.2，kx=1，ky=1.5，p=1，图1a）和图1b）中cx=cy=0.02，图1c）中cx=cy=0.5.图1a）中kz=1.2，由公式得 ωx= 0.59，满足条件 kz≈2ωx，光束中心沿x方向的振荡幅度随传输距离的增加而先指数增长；图1b）中kz=1.8，由公式得 ωy= 0.89，满足条件 kz≈2ωy，光束中心沿y方向的振荡幅度随传输距离的增加而先指数增长；图1c）中kz=3，不满足条件 kz≈2ωx或 kz≈ 2ωy，光束中心按不同的频率等幅周期振荡.

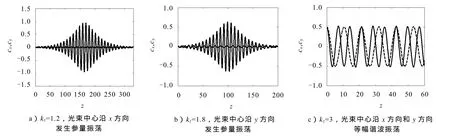
图1 α=β= 0，有纵向调制且光束中心初始偏离二坐标轴均很小时的演化轨迹

3.3 解析结果与数值模拟结果的比较

为验证解析结果的正确性，下面将利用分布傅里叶方法[17]对非局域非线性薛定谔方程（1）进行数值模拟，设初始输入具有形式（4），且响应函数具有椭圆高斯型分布定义非局域程度（a为光束初始束宽，u为非局域非线性响应函数的特征宽度），χ越小，非局域程度越强，反之越弱.为数值模拟方便，我们假设非局域程度且

3.3.1 无纵向调制时光束中心演化的数值模拟结果

图2给出了μ=0，入射功率满足条件 P0=Pcx=Pcy时若光束中心偏离x轴和y轴很小时数值模拟和数值积分结果的对比.图2a）中kx=ky=1，即光束中心沿x轴和y轴具有相同的振荡周期；图2b）中kx=1，ky=1.2，光束中心沿x轴和y轴具有不同的振荡周期.为验证解析结果的正确性，现以图2b）为例，由解析结果可得光束中心在x方向上的振荡频率为而由数值模拟可得其频率为 0.500，数值积分则给出结果 0.483；解析结果得光束中心在 y方向上的振荡频率为而由数值模拟可得其频率为0.59，数值积分则给出结果0.57.由此可知，我们的解析结果和数值结果吻合得很好.

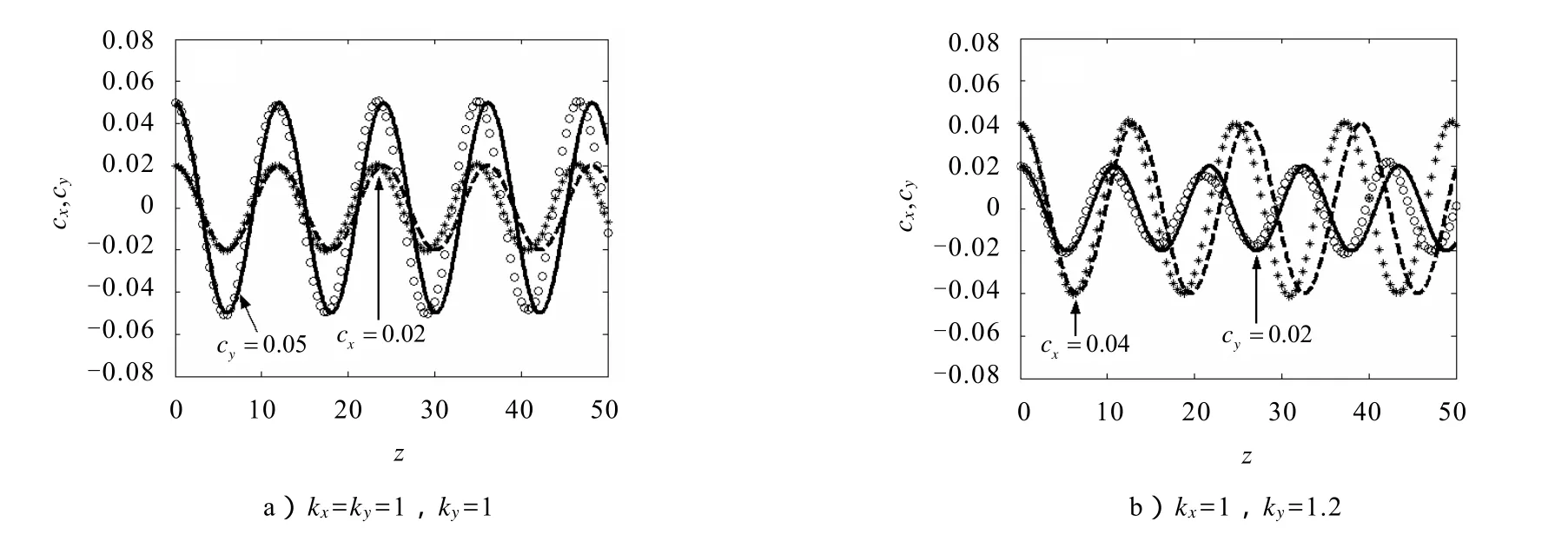
图2 p=0.5， α=β= 0，无纵向调制且光束中心初始偏离各坐标轴均很小时的演化规律

图3给出了μ=0且入射功率满足条件 P0= Pcx= Pcy时若光束中心的数值模拟和数值积分结果的对比.由图3a）和图3b）可得两横向调制频率相等，即 kx=ky= 1，且光束中心初始偏离x轴较大而偏离y轴很小，则光束在演化的过程中其中心在周期振荡的同时，振荡幅度沿y方向指数增长逐渐而沿x方向指数衰减，即光束在传输过程中其能量将由一个偏振方向转移到另外一偏振方向，产生共振现象.图3c）中kx=1，ky=1.2，即两横向调制频率不同，则光束中心将分别作不同频率的等幅周期振荡.由以上结果可得在数十个瑞利距离内我们的数值模拟结果和数值积分结果吻合得很好.

图3 p=0.5， α=β= 0，无纵向调制且光束中心初始偏离x轴较大(c x =0.8)而偏离y轴较小(c y= 0.08)时的传输规律

3.3.2 有纵向调制时光束中心的演化特征

有横向和纵向调制时光束中心分别沿x轴和y轴的演化规律如图4所示.图4显示了光束具有初始中心分布cx=0.02，cy=0.2，初速度 α=β= 0，当μ=0.1，kx=1，ky=kz=1.2，p=0.5且 P0=Pcx=Pcy时，其数值模拟结果和数值积分结果的对比.从中可得 kx≠ky时，光束中心分别沿x轴和y轴作不同周期的振荡，且由于满足条件kz≈2ωy，所以光束中心沿y轴的振荡幅度随着传输距离的增加指数增长.

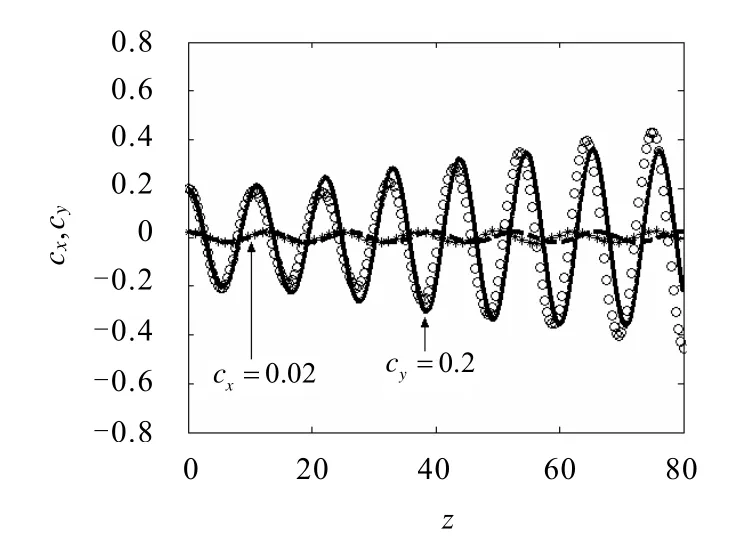
图4 有横向和纵向调制时光束中心分别沿x轴和y轴的演化规律

4 结论

利用有效粒子方法，根据带有纵向和横向周期调制函数的非局域非线性薛定谔方程，分析得出了椭圆高斯格中光孤子中心的演化规律.理论分析和数值模拟都证明，在具有纵向和横向折射率周期性调制的克尔型非线性介质中，介质的纵向和横向调制频率、纵向和横向调制深度等参数是影响椭圆高斯光束中心传输的重要因素，因此，要使光束按不同的规律进行传输，则需要调整相应的参数.这些结果对全光开关和路由等光控制技术的研究和应用具有重要意义.

[1]SNYDER A W,MITCHELL D J.Accessible solitons[J].Science,1997,276(6)：1538-1541.

[2]PECCIANTI M,CONTI C，ASSANTO G,et al.All-optical switching and logic gating with spatial solitons in liquid crystals[J].Appl Phys Lett,2002,81(18)：3335-3337.

[3]CONTI C,PECCIANTI M,ASSANTO G.Route to nonlocality and observation of accessible solitons[J].Phys Rev Lett,2003,91(7)：073901-1-4.

[4]CONTI C,PECCIANTI M,ASSANTO G.Observation of optical spatial solitons in a highly nonlocal medium[J]. Phys Rev Lett,2004,92(11)：113902-1-4.

[5]FRATALOCCHI A,ASSANTO G.All-optical switching in a liquid crystalline waveguide[J].Appl Phys Lett, 2005,86(5)：051109-1-3.

[6]GUO Qi,LUO Boren,YI Fahuai,et al.Large phase shift of nonlocal optical spatial solitons[J].Phys Rev：E, 2004,69(1)：016602-1-8.

[7]QIN Xiaojuan,GUO Qi,HU wei,et al.Strongly nonlocal elliptical spatial optical solion[J].Acta Optica Sinica, 2006,55(3)：1237-1243.

[8]ZHONG Weiping,YI Lin.Influence of linear focusing and defocusing effects on interaction between spatial solitons[J].Acta Optica Sinica,2008,28(5)：960-964.

[9]WANG Yuqing,GUO Qi.Rotating soliton clusters in nonlocal nonlinear media[J].China Phys：B,2008,17(7)：2527-2534.

[10]CHEN Susong.Two-dimensional self-similar soliton wave in highly nonlocal media[J].Acta Optica Sinica, 2009,29(6)：1653-1658.

[11]ZHOU Jun,REN Haidong,Feng Yaping.The pulsating propagation of spatial soliton in strongly nonlocal optical lattice[J].Acta Physica Sinica,2010,59(6)：3992-4000.

[12]WANG Yuqing,ZHONG Dongzhou,HUANG Dong.Influence of phase-front curvature for an optical beam in strongly nonlocal media[J].Acta Optica Sinica,2010,30(8)：2377-2382.

[13]KARTASHOV Y V,TORNER L,VYSLOUKH V A.Parametric amplification of soliton steering in optical lattices[J].Opt Lett,2004,29(10)：1102-1104.

[14]KARTASHOV Y V,VYSLOUKH V A,TORNER L.Oscillations of two-dimensional solitons in harmonic and Bessel optical lattices[J].Phys Rev：E,2005,71(3)：036621-1-5.

[15]DAI Zhiping,WANG Yuqing,GUO Qi.Mobility of strongly nonlocal solitons in optical lattices[J].Phys Rev：A,2008,77(6)：063834-1-5.

[16]SANTHANAMA J,AGRAWAL G P.Raman-induced spectral shifts in optical fibers general theory based on the moment method[J].Opt Commun,2003,222：413-420.

[17]AGRAWAL G P.Nonlinear fiber optics[M].3th edition.Beijing：Acade mic Press,2001：51-55.

Oscillations of Two-Dimensional Strongly Nonlocal Solitons in Optical Lattices

WANG Yu-qing,ZHONG Dong-zhou,HUANG Dong,WANG Tian-lei
(School of Information Engineering,Wuyi University,Jiangmen 529020,China)

The evolution of elliptically Gaussian beam in the strongly nonlocal nonlinear media with longitudinal and transverse periodic modulations of the linear refractive index is studied by employing the effective-partical approach.The propagation properties for the beam center are obtained in the different modulations.The analytical and numerical results are shown in the case of no longitudinal modulation:The same(different)frequency of transverse modulation will lead to the same(different) oscillating period for the beam center when the initial beam center displacement along the transverse axes is small;but when the initial beam center displacement along a certain transverse axes is very large,the beam center will oscillate periodically with the amplitude unchanged;if the transverse modulation frequencies are not equal,the beam center will oscillate periodically;and the amplitude of the small (large) initial beam center displacement along the transverse axes decreases(grows)exponentially if transverse modulation frequency is the same.In the case of the longitudinal periodic modulation,if the relation of the longitudinal modulation frequency and some transverse refractive-index modulation frequency condition is satisfied,the oscillation amplitude of the beam center will grow exponentially along this very transverse direction with the propagation distance,and decrease later.But if the frequency condition is not satisfied,the beam center will oscillate periodically with amplitude unchanged.

nonlinear optics;nonlocal nonlinear Schrödinger equation;effective-partical approach; spatial optical soliton

?

O437.5

A

1006-7302（2011）03-0001-06

2011-04-15

广东高校优秀青年创新人才培育资助项目（30717003）；五邑大学青年基金资助项目（201005132036437）

王玉青（1982—），女，河南临颍人，讲师，硕士，研究方向为非线性光学传输.