一种改进的PSO网格调度算法

杨长兴，胡 金

（中南大学 信息科学与工程学院，湖南 长沙410083）

在网格计算中，任务管理、任务调度和资源管理是网格的3个基本功能。任务调度是网格系统的一个关键问题，关系到网格能否高效利用资源、快速完成任务以及实现系统负载均衡。同时它也是一个NP完全问题[1]，即得到一个最优的调度方案或是在有限的时间里找出最优(任务,资源)的匹配方案是不可能的。目前多采用启发式算法解决此类问题。

近年来，很多学者将启发式算法应用于任务调度中，并取得了较好的研究成果[2-5]。其中，GA算法可能找到最优解，但选择过程存在随机性，不能确保得到最优解，同时开销大，运行时间长；AA算法虽然有正反馈机制能避免早熟现象，但容易收敛于局部最优，而且算法复杂，搜索时间长；SA算法能以一定的概率接受差的解而可能跳出局部极小，是一种全局最优算法，但是搜索时间比较长；PSO粒子群优化算法[6]搜索速度快、操作简单、效率高，但是易陷入局部极值，搜索精度不高。

针对PSO易早熟、求解质量不高的问题，为实现最小化任务完成总时间(makespan)，本文提出一种基于独立任务调度的改进PSO网格调度算法MCPSO(An improved PSO of grid scheduling algorithm under the meta task)。该算法的主要思想是：首先采用混沌[7]序列初始化粒子的位置，并在产生的大量粒子中择优选出初始种群；然后在粒子更新时引入混沌搜索，随机产生若干混沌序列并把最优混沌序列得到的位置和当前粒子最优位置比较，如果优于当前粒子，则更新当前粒子的最优位置，引导当前粒子跳出局部最优点，快速寻找最优解。实验表明，该算法改善了PSO算法易陷入局部最优问题，同时兼顾更好的makespan和负载均衡，有效提高网格的性能。

1 问题定义

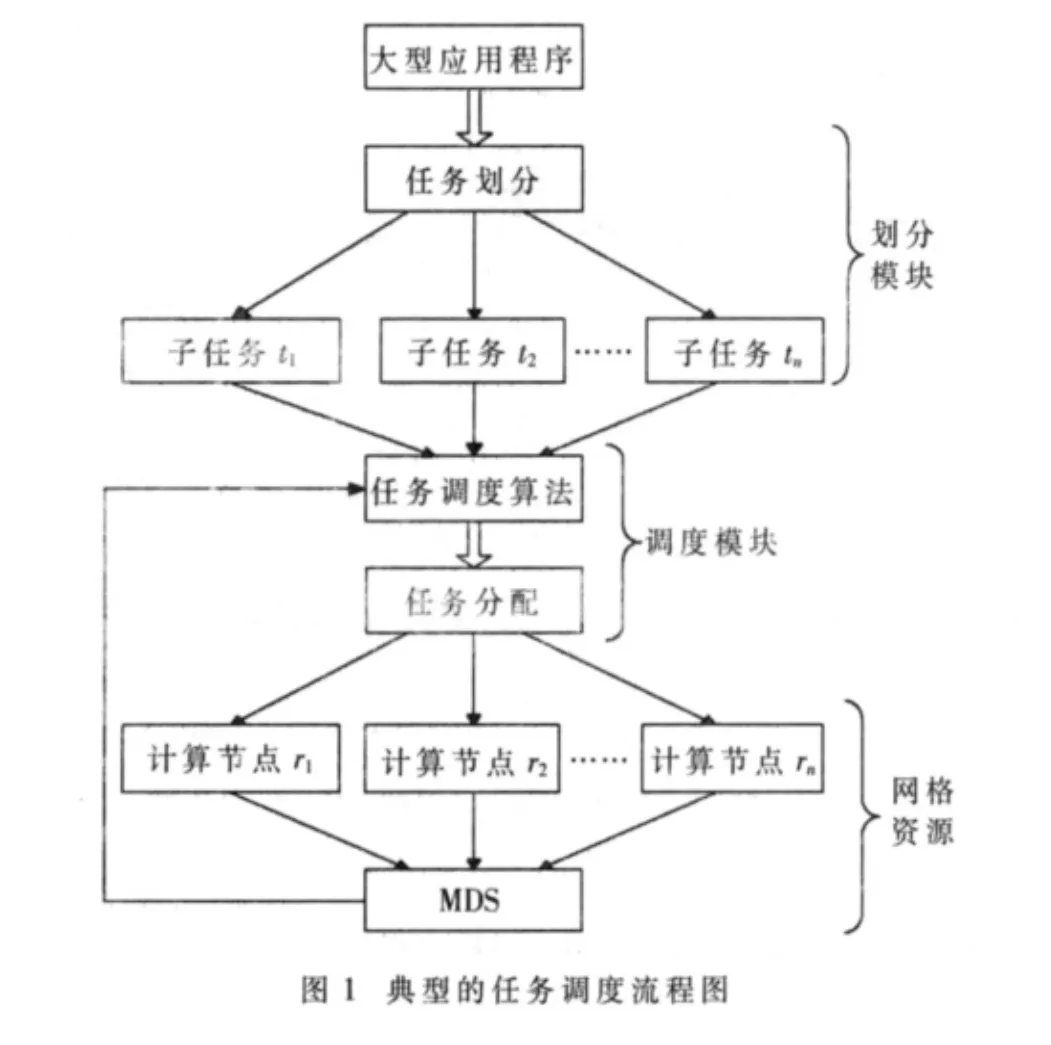
图1所示是一个简单的任务调度流程图，其中MDS(Monitoring and Discovering Service)是资源监控与发现服务，用于收集和发布系统状态信息。

如图1所示，首先任务划分模块将应用程序划分为若干个子任务，然后调度模块从网格资源中的信息采集模块MDS收集必要信息，最后按一定的策略对任务进行分发。

通常在网格环境下主要考虑一组相互独立、任务之间没有数据和通信依赖的独立任务(metatask)。目前多数研究是基于此展开的。本文将主要研究独立任务调度。

现假定虚拟组织VO中用户提交了若干个任务，这些任务经由图1中的划分模块分成n个独立子任务t1、t2、…、tn组成子任务集合 T，网格系统中有 m个节点(网格资源)r1、r2、…、rm构成资源集合R。任一任务 ti可以在任一节点rj上执行，rj在同一时刻只能处理一个任务，而 ti不能同时在两个节点上执行，ti一旦开始，rj被独占，直到ti完成后才能执行其他任务。用一个n维向量(w1，w2，…，wn)表示任务的预计完成时间，其中 wi为任务i的预计完成时间。

定义1(任务映射集)n个任务映射到m个节点的映射方案T→R集合即任务映射集MAP。集合MAP={map1，map2，…，mapn}，其中 mapi表示第 i个任务在映射到的节点mapi上执行。

定义2(节点工作时间)节点工作时间RCj是指节点j处理完所有分配给它的任务所花费的时间。如式(1)所示：

定义 3(时间跨度)时间跨度即 makespan，是指任务集合T中第一个任务开始执行到最后一个任务完成的时间。在某调度算法下的makespan也称为该算法的调度长度，makespan越小，调度策略越好。最优跨度ω为网格当前实际跨度的最好值，最优调度的下界是将任务平均分到各个计算资源上，此时得到的ω值为理论最优跨度ωmin即均衡负载。

定义4(负载均衡度)计算资源上的任务称为负载。当计算资源上的负载超过ωmin时该计算资源为重载资源，而当负载低于ωmin时为轻载资源。任务调度的目标是最小化资源上的负载，使得各个资源负载基本相同，这个过程也称为负载均衡。负载均衡度β按式(5)计算，表示计算资源负载偏离均衡负载ωmin的程度，其数值越小，网格系统就越均衡。

独立任务调度的数学模型为：

2 改进PSO的网格调度算法

2.1 标准PSO算法

粒子群优化算法PSO(Particle Swarm Optimization)是由Eberhart和Kennedy于1995年发明的一种全局迭代优化算法。PSO先生成初始种群，即在可行解空间中随机初始化一群粒子，每个粒子代表着优化问题的一个潜在可行解。每个粒子将在解空间中“飞行”，并由一个速度决定其方向和距离。通常粒子将追随当前的最优粒子而动，并经过多次迭代得到最优解。在每一次迭代时，粒子将跟踪两个极值，一为粒子本身迄今找到的最优解pbest，另一个为全种群迄今找到的最优解gbest。

每一代粒子速度和位置更新公式如下：

式中，vij(t)、vij(t+1)表示第 i个粒子在第 j维方向上的当前速度和更新后的速度；xij(t)、xij(t+1)表示第i个粒子在第j维方向上的当前位置和更新后的位置；w为惯性因子，作用是控制和提高优化效率；c1、c2为学习因子，通常在 0～2 间取值；r1～U(0，1)，r2～U(0，1)为两个相互独立的随机函数；pij(t)表示第i个粒子经历过的最好位置矢量即个体最好位置在第j维方向上的位置；pgj(t)表示群体中所有粒子经历过的最好位置矢量即全局最好位置在第j维方向上的位置。

2.2 混沌优化

由确定的运动方程得到的具有随机性的运动状态称为混沌运动。混沌是自然界中一种常见现象，其变化过程看似杂乱无章，但不是完全混乱，而是有一定的规律性。将方程中呈混沌状态的变量称为混沌变量，混沌变量对初值十分敏感。混沌变量具有从任意点(除不动点)出发，按确定公式遍历所有状态的特点，即确定性、遍历性，表现形式如同随机变量。一个典型的混沌系统是Logistic方程，其表达式为：式中，μ 为控制参数，0≤μ≤4；un∈[0，1]。

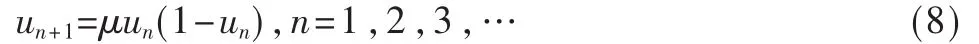
混沌搜索的主要思想是通过混沌系统如式(7)产生混沌序列，然后通过载波的方式

将其映射到优化空间中，也就是将混沌变量的值域“放大”到优化变量的取值范围内。

2.3 改进PSO的网格调度算法(MCPSO)

PSO具有很强的全局搜索能力，但不能保证全局收敛。当粒子自身信息和个体极值信息占优时，往往停滞于局部最优解，且随机初始化的种群质量不高，甚至距离最优解位置较远。而混沌具有良好的遍历性、随机性以及一定的突跳能力，易跳出局部极值点，最终可能得到最优解。

因而可以利用混沌的遍历性，在初始化时产生大量粒子，从中择优选出初始种群。同时在粒子位置和速度更新时，引入混沌搜索，并把最优混沌序列得到的位置与当前粒子最优位置相比较，如果优于当前粒子则进行替换。这样可以有效减少算法收敛于局部极值的现象。算法流程如下：

(1)给定种群大小 POPSIZE、最大迭代次数、惯性权值 w、学习因子 c1、c2及控制参数 μ等。

(2)混沌初始化：

①随机产生一个n维每个分量数值在[0，1]上的向量，z1=(z11，z12，…，z1n)，n 为种群的大小，根据式(8)，得 n个混沌序列 z1，z2，…，zn。

②利用式(9)将 zi，1≤i≤n分量载波到相应的变量取值区间，选出较优的POPSIZE个粒子作为初始种群。

(3)随机初始化各个粒子的初始速度并计算其适应值，设置各个粒子的初始极值并计算种群极值。

(4)根据式(6)、式(7)更新粒子位置和速度。

(5)启动混沌搜索。随机产生d个[0，1]上的随机数，根据式(8)得到d个混沌序列，并把产生的混沌序列依次载波放大到对应变量的取值范围上，从中选出最优位置。

(7)更新个体极值和群体极值。

(8)跳至步骤(4)直到算法到达最大迭代次数。

(9)输出全局最优值和全局最优粒子、最优跨度ω、负载平衡度β。

2.4 问题编码

对于n个任务m个资源的调度，粒子的位置和速度均用n维向量表示，维数和任务数一致。如位置向量(x1，x2，…，xm)中第 i维分量 xi表示任务 ti的权值，是[0，m)之间的一个随机数。当n=10，m=5时，各个节点对应的权值范围如表1。

表1 权值与节点序号对应表

若某粒子的位置矢量表示如下：

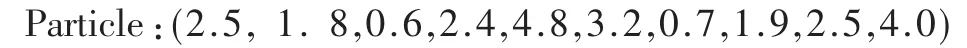
上述粒子即为任务的一个调度方案，由表1可得任务与节点的映射关系如表2所示。

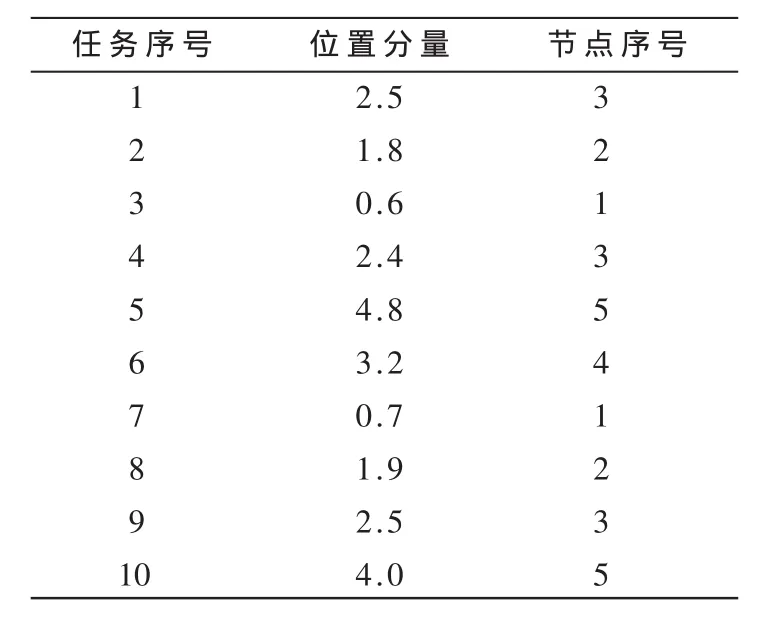
表2 基于节点编码的任务分配方案

3 实验与性能分析

以GridSim工具包为基础构建网格仿真环境，将本文提出的MCPSO算法与基于独立任务的基本粒子群优化算法MPSO算法进行对比分析。

PSO算法参数设置如下：种群大小POPSIZE=10，学习因子c1=c2=2.05，惯性因子ω=0.729，算法最大迭代次数为 1 000，混沌控制参数 μ=4。测试运行 50次，取 50次实验的平均结果作为实验结果。

实验中有5个节点，10个任务，各个任务的预计完成时间{10,42,34,27,56,79,77,62,81,51}，单位为 s。

实验从调度方案的求解质量、makespan、负载平衡度3个方面比较两种算法的性能。

求解质量如表3所示。

表3 实验结果比较

比较可知，本文提出的MCPSO算法比MPSO有更好的性能，平均跨度值与最好解的偏差小，最好解的次数明显多于MPSO算法，最差解也明显优于MPSO，MCPSO算法的求解质量更好。

为了观察算法的收敛特性，给出了两种算法1 000次迭代的makespan变化曲线，如图2所示。从图2可以看出，MCPSO算法收敛速度优于MPSO算法的情况，并能得到更好的解，而且改进的PSO算法初始解明显更优。

由图3可知，两种算法的负载均衡度随着迭代次数的增加而减少，即负载均衡性能都有提升。而MCPSO算法的负载均衡性能大大好于MPSO算法。

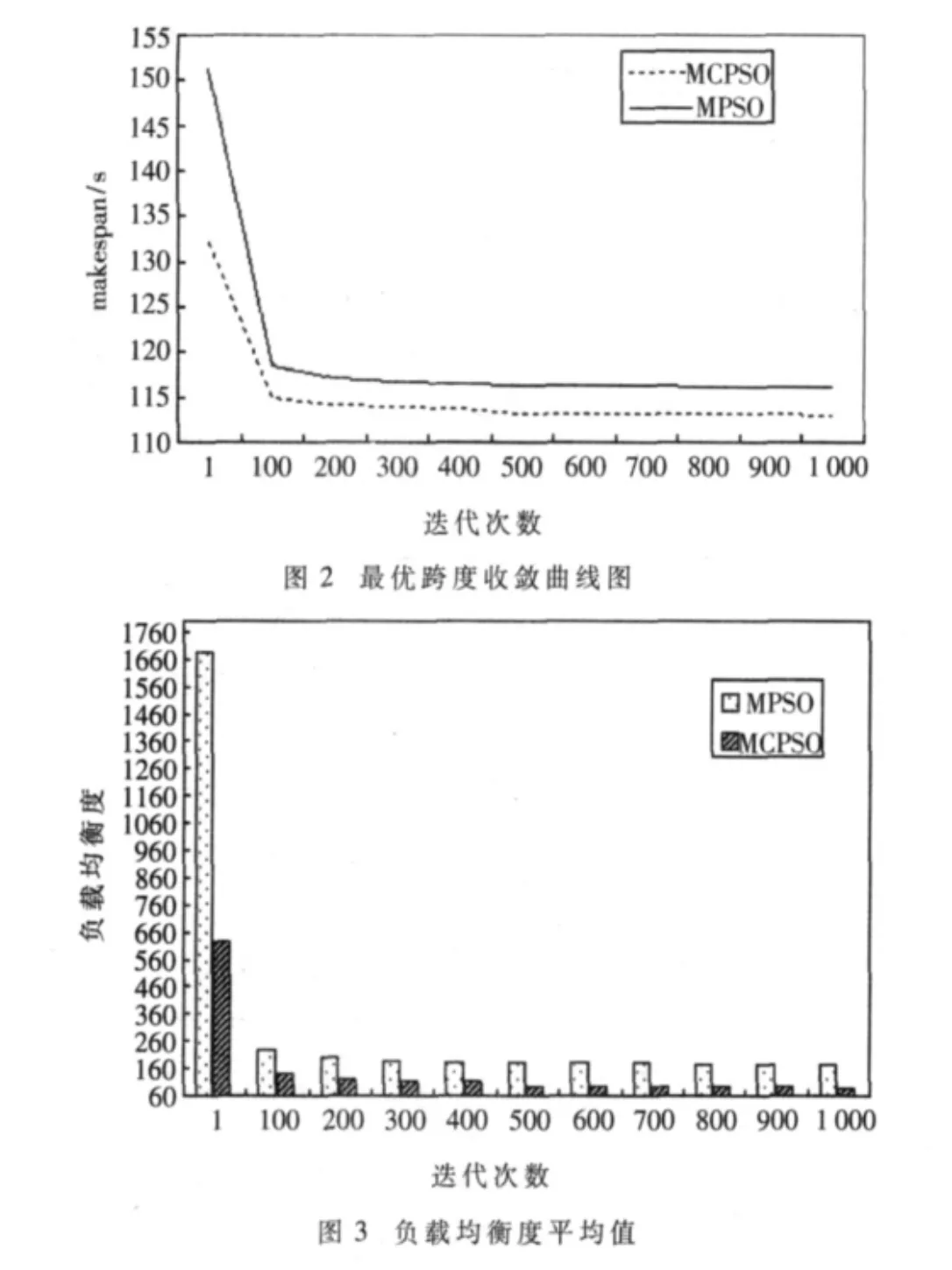
通过实验可以看出，基本粒子群能快速地找到较优解，但是后期逐渐收敛于该解，并处于“停滞”状态，很难得到更优解。引入混沌机制的MCPSO算法，拥有基本粒子群算法快速收敛的特性，同时在未得到最优解的情况下，逐渐向最优解靠近，不断得到更优解甚至最优解。

为改善网格调度性能，本文提出了基于独立任务的改进PSO任务调度算法。该算法以时间跨度makespan为数学模型，结合粒子群算法和混沌优化原理，首先通过混沌初始化得到较优的初始种群，有效减少粒子飞向较优点的迭代次数；在更新粒子位置和速度时，对粒子的最优位置进行混沌搜索，试图找出更优的位置，使粒子飞向更优位置而避免陷入局部最优位置。实验表明，与基本粒子群算法MPSO相比，MCPSO算法能有效提升任务调度问题的求解质量，缩短了makespan，优化了计算节点的负载均衡性能。下一步的研究工作是在关联任务调度时，如何利用该算法有效提高任务调度的效率，以及如何让算法在当网格系统中用户的实际需求多样化时仍然有效。

[1]Dong Fangpeng,SELIM G.Scheduling algorithms for grid computing:state of the art and open problems[D].Technical Report.School of computing,Queen′s University.Kingston,Ontario,January,2006.

[2]贺晓雨.一种用于任务调度的广义遗传算法[J].计算机工程,2010,36(17):184-186.

[3]AGHDAM H,PAYVAR S.A Modified simulated annealing algorithm for static task scheduling in grid computing[C].International Conference on Computer Science and Information Technology，2008:623-627.

[4]Zhang Lei,Chen Yuehui,Yang Bo.Task scheduling based on PSO algorithm in computational grid[M].Intelligent System Design and Applications，2006.

[5]魏东，吴良杰，佐丹，等.基于混合蚁群算法的网格任务调度[J].计算机工程,2010,36(3):215-217.

[6]KENNEDY J,EBERHART R.Particle Swarm Op-timization[C].In proc.IEEE Int Conf on Neural Networks.Perth,1995.

[7]李兵,蒋慰孙.混沌优化方法及其应用[J].控制理论与应用,1997,14(4):613-615.